?博主主頁:?碼農派大星.

關注博主帶你了解更多數據結構知識

---

1.非遞歸的前序遍歷

1.用棧來實現

2,前序遍歷是根左右, 先是根節點入棧,,然后不為空時向左遍歷,當為空時就返回向右遍歷,右為空時直接出棧,依次循環即可.

public void preOrderNot(TreeNode root){Stack<TreeNode> stack = new Stack<>();if(root==null){return;}TreeNode cur = root;while (cur != null || !stack.isEmpty()){while (cur != null){stack.push(cur);System.out.print(cur.val + " ");cur = cur.left;}TreeNode top = stack.pop();cur = top.right;}}

2.非遞歸的中序遍歷

1和前序遍歷不同的是,中序遍歷是左根右

2先讓左節點入棧,一直往左遍歷,直到遇到空時,返回根節點,再向右一直遍歷,遇到右為空時,出棧.

public void inOrderNot(TreeNode root) {Stack<TreeNode> stack = new Stack<>();if(root==null){return;}TreeNode cur = root;while (cur != null || !stack.isEmpty()) {while (cur != null) {stack.push(cur);cur = cur.left;}TreeNode top = stack.pop();System.out.print(top.val + " ");cur = top.right;}}

3.非遞歸的后序遍歷

后序遍歷是左右根,我們先讓左節點入棧,再一直向左遍歷,當為空的時候需要peek一下判斷右節點是否為空，如果右節點為空則出棧，如果右節點不為空那么遍歷右節點.

注意:

當右節點不為空遍歷右節點的時候，可能造成死循環，所以我們需要定義一個prev值來表示最后一個被打印的節點。

 public void PostOrderNot(TreeNode root) {Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;TreeNode prev = null;while (cur != null || !stack.isEmpty()) {while (cur != null) {stack.push(cur);cur = cur.left;}TreeNode top = stack.peek();if (top.right == null || top.right == prev) {//打印當前top 并彈出stack.pop();System.out.print(top.val + " ");prev = top;} else {cur = top.right;}
}

4.根據二叉樹創建字符串OJ鏈接

給你二叉樹的根節點?root?，請你采用前序遍歷的方式，將二叉樹轉化為一個由括號和整數組成的字符串，返回構造出的字符串。

空節點使用一對空括號對?"()"?表示，轉化后需要省略所有不影響字符串與原始二叉樹之間的一對一映射關系的空括號對。

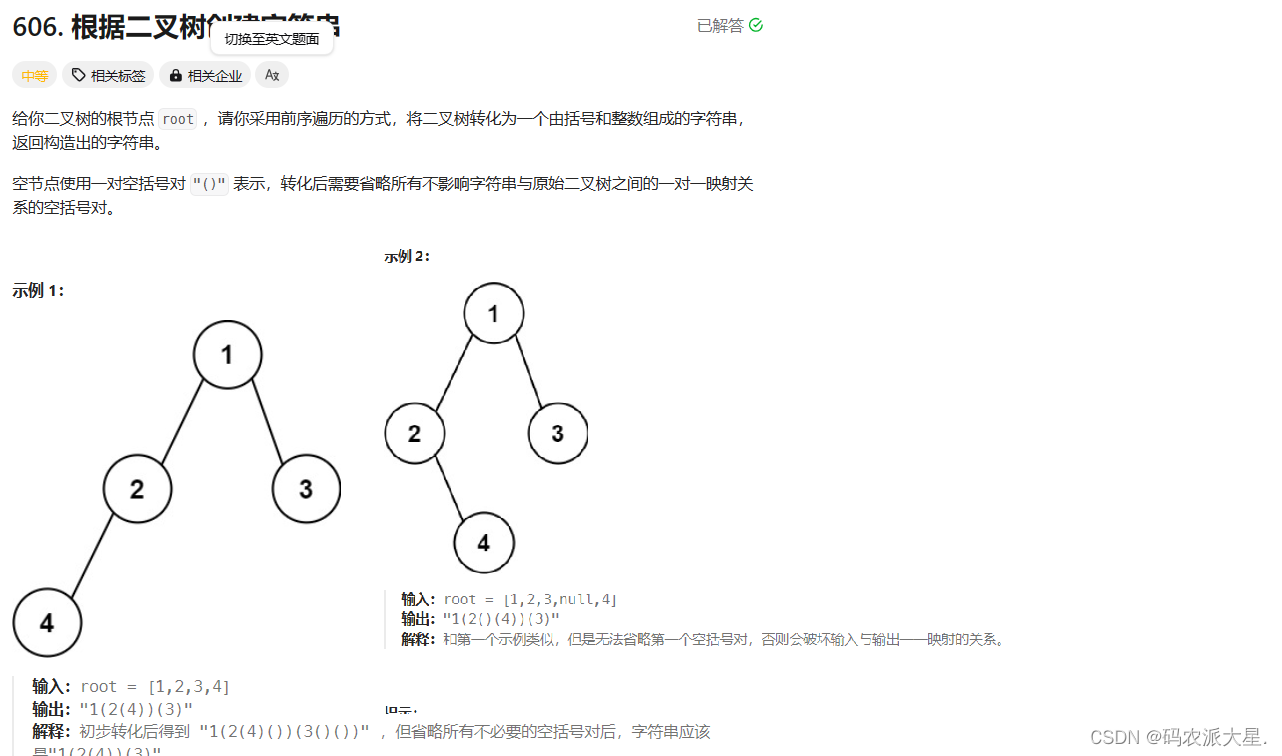
解題:先遍歷左 如果左不為空為(root.left),如果為空,判斷右是否為空,如果為空(就是左右都為空)什么都不返回,不為空返回()

再處理右樹,如果為空什么都不返回,如果不為空返回(root.right)

class Solution {public String tree2str(TreeNode root) {StringBuilder stringBuilder = new StringBuilder();tree2strChild(root,stringBuilder);return stringBuilder.toString();}private void tree2strChild(TreeNode root,StringBuilder stringBuilder){if(root == null)return;stringBuilder.append(root.val);if(root.left != null){stringBuilder.append("(");tree2strChild(root.left,stringBuilder);stringBuilder.append(")");}else{//左邊為空 右也為空if(root.right == null){return;}else{stringBuilder.append("()");}}//處理root右樹情況if(root.right == null){return;}else{stringBuilder.append("(");tree2strChild(root.right,stringBuilder);stringBuilder.append(")");}      }
}

?5.根據一棵樹的前序遍歷與中序遍歷構造二叉樹OJ鏈接

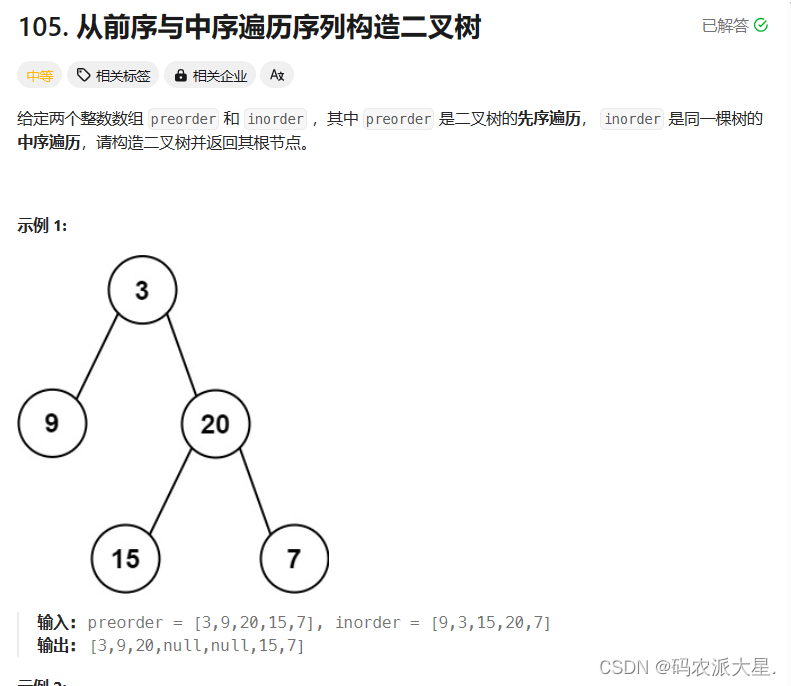
class Solution {public int preIndex;public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChilde(preorder,inorder,0,inorder.length-1);   }private TreeNode buildTreeChilde(int[] preorder,int[] inorder,int inBegin,int inEnd){if(inBegin > inEnd){return null;}        TreeNode root = new TreeNode(preorder[preIndex]);int rootIndex = findRootIndex(inorder,inBegin,inEnd,preorder[preIndex]);  preIndex++;root.left = buildTreeChilde(preorder,inorder,inBegin,rootIndex-1);root.right = buildTreeChilde(preorder,inorder,rootIndex+1,inEnd);return root;}private int findRootIndex(int[] inorder,int inBegin,int inEnd,int Key){for(int i = inBegin; i<= inEnd;i++){if(inorder[i] == Key){return i;}}return -1;}
}

?6.根據一棵樹的中序遍歷與后序遍歷構造二叉樹OJ鏈接

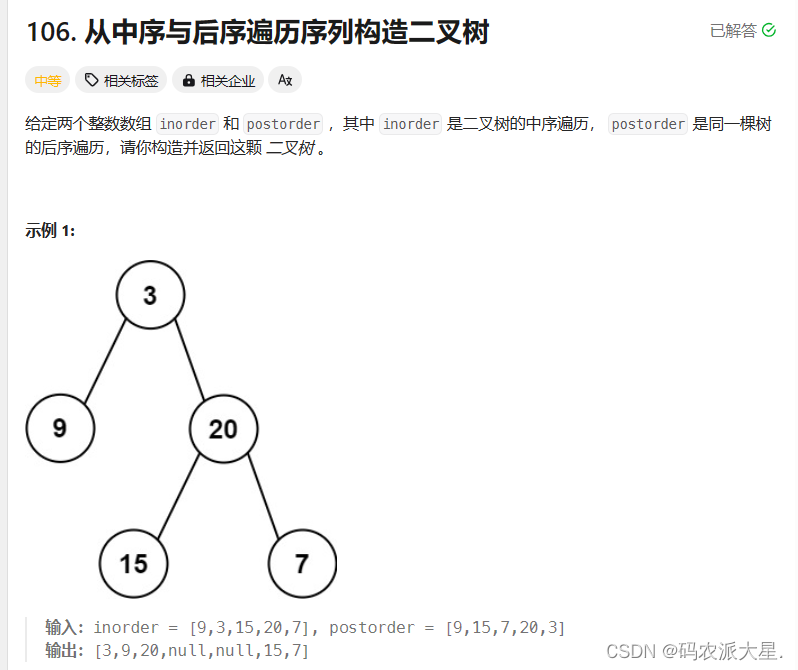
class Solution {public int  postIndex = 0;public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex = postorder.length-1;return buildTreeChild(inorder,postorder,0,inorder.length-1);}private TreeNode buildTreeChild(int[] inorder,int[] postorder,int inBegin,int inEnd){if(inBegin > inEnd){return null;}TreeNode root = new TreeNode(postorder[postIndex]);int rootIndex = findRootIndex(inorder,inBegin, inEnd,postorder[postIndex]);postIndex--;root.right = buildTreeChild(inorder,postorder,rootIndex+1,inEnd);root.left = buildTreeChild(inorder,postorder,inBegin,rootIndex-1);return root;}private int findRootIndex(int[] inorder,int inBegin,int inEnd,int Key){for(int i = inBegin; i<= inEnd;i++){if(inorder[i] == Key){return i;}}return -1;}
}