機器學習【二】KNN

? KNN算法是一種基于實例的惰性學習算法，其核心思想是通過"多數投票"機制進行分類決策。算法流程包括數據準備（需歸一化處理）、距離計算（常用歐氏距離）、選擇K值（通過交叉驗證確定）和決策規則（分類用投票，回歸取平均）。KNN具有簡單直觀、無需訓練等優點，但也存在預測速度慢、高維效果差等缺點。實際應用中需注意K值選擇、樣本不平衡等問題，可通過距離加權、自適應K值等方法優化。文中以鳶尾花分類為例展示了KNN的實現過程，并通過可視化展示了不同K值對決策邊界的影響。

1 介紹

? ? ? ?案例導學：假設你剛搬到一個新城市，正在尋找一個好的餐館吃晚餐。你可能會詢問你的鄰居們推薦一個好的餐館。如果大多數鄰居推薦同一家餐館，你可能會認為這家餐館的確不錯，并選擇去那里用餐。在這個例子中，你在做一個決策，而你的決策基于你的鄰居們的意見或“投票”

?要義：K - 最近鄰居（KNN）算法是一種基于實例的學習，它用于分類和回歸。在分類中，一個對象的分類由其鄰居的“多數投票”決定，即對象被分配到其K個最近鄰居中最常見得到類別中。投票規則是整個算法最核心的部分。（K值維度距離）?KNN算法在機器學習領域的重要性主要體現在它的直觀性、易理解性和在某些場合（如小規模數據、低緯度問題）下的有效性

?KNN是一種??惰性學習算法??，核心步驟：

計算目標點與所有樣本點的距離
選取距離最近的K個樣本
通過投票（分類）或平均值（回歸）得出結果

2 KNN實現流程

步驟分解??：
??數據準備??
數值型特征歸一化（避免量綱影響）
處理缺失值（KNN對缺失值敏感）
??距離計算??
常用歐氏距離（見第4節）
??選擇K值??
通過交叉驗證選擇最優K（通常取3-10的奇數）
? ? ? ? （交叉驗證：將樣本按照一定比例拆分成訓練和驗證用的數據從一個較小的K值開始? ? ? ? ? ? ? ?不斷增加然后驗證集合的方差最終找一個比較合適的K值）
??決策規則??
分類：多數投票法
回歸：K個樣本的平均值

3 KNN注意事項

注意事項	原因與解決方案
??數據歸一化??	不同特征量綱不同會導致距離計算偏差，需標準化
??K值選擇??	K太小易受噪聲影響，太大導致欠擬合（用網格搜索優化）
??樣本不平衡??	多數類主導投票（解決方案：加權投票）
??高維災難??	維度過高時距離失去意義（需特征選擇/降維）
??計算效率??	需存儲全部數據，預測慢（優化：KD樹、球樹）

# 觀察不同K值對準確率的影響
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用于正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False # 用于正常顯示負號k_values = range(1, 15)
accuracies = []
for k in k_values:knn = KNeighborsClassifier(n_neighbors=k).fit(X_train, y_train)accuracies.append(knn.score(X_test, y_test))# 繪制曲線（通常出現"倒U型"）plt.plot(k_values, accuracies)
plt.xlabel('K值'); plt.ylabel('準確率')
plt.show()  # 選擇準確率最高的K值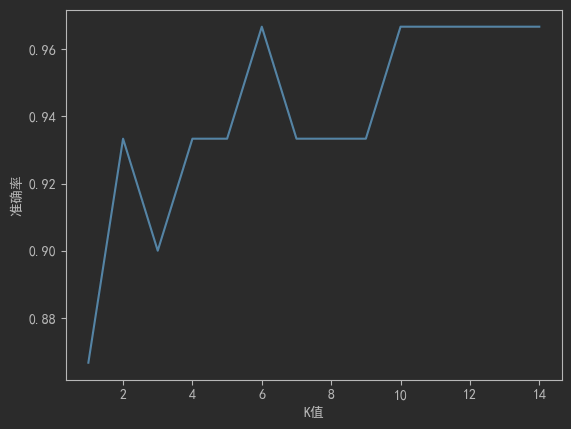

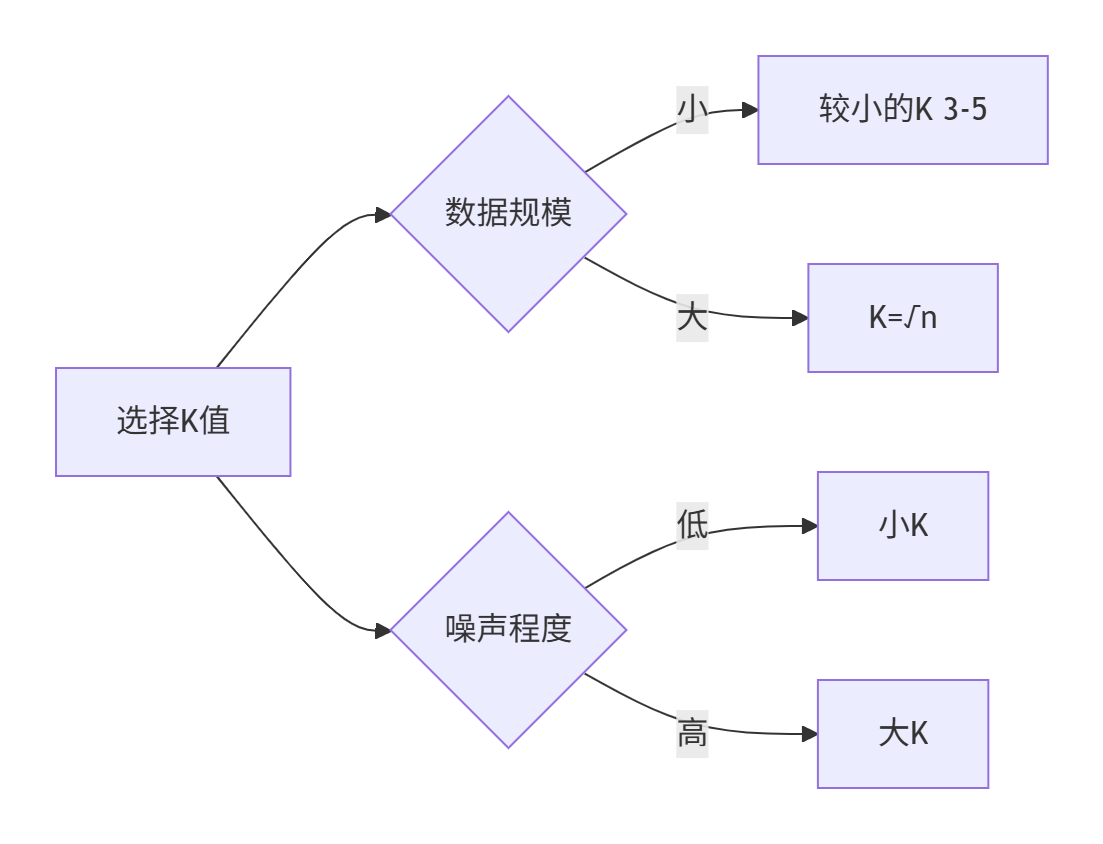?K值選擇

4 KNN常用距離

距離類型	公式	適用場景
??歐氏距離??	√Σ(x_i - y_i)2	連續數值特征（最常用）
??曼哈頓距離??	Σ\|x_i - y_i\|	稀疏特征（如文本分類）
??余弦相似度??	(A·B)/(\|A\|\|B\|)	方向差異＞大小差異（如推薦系統）
??閔可夫斯基距離??	(Σ\|x_i - y_i\|^p)^(1/p)	歐氏/曼哈頓的泛化形式

??注??：公式中?x_i,?y_i表示兩個樣本的第i個特征值

5 KNN優缺點

5.1 優缺點分析

優點??：

? 簡單直觀，適合多分類

? 無需訓練（實時學習）

? 耗時短模型訓練速度快

? 對數據分布無假設

? 對異常值不敏感

??缺點??：

? 預測速度慢（需遍歷所有樣本）

? 對異常值敏感

? 維度過高時效果差

? 需要大量內存存儲數據

5.2 變體和演進

??距離加權KNN??：給更近的鄰居賦予更大權重

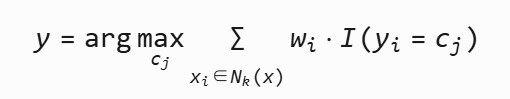
?權重?wi?=d(x,xi?)21?或?exp(?d(x,xi?))

??自適應KNN??：不同區域使用不同K值（密集區域用小K，稀疏區域用大K）

??KNN回歸??：對連續目標的預測取近鄰平均值

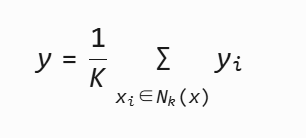
5.3 與其他模型的對比

算法	訓練速度	預測速度	適用場景	與KNN主要差異
KNN	O(1)	O(n)	小規模數據、低維度	-
決策樹	O(n logn)	O(深度)	大規模數據	全局決策 vs 局部決策
SVM	O(n3)	O(支持向量數)	高維數據	最大邊距超平面 vs 最近鄰
神經網絡	O(epoch×n)	O(層數)	復雜模式	特征自動提取 vs 原始特征距離

6 項目使用

6.1 體驗項目

# 體驗項目
from sklearn.neighbors import NearestNeighbors
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Dplt.rcParams['font.sans-serif'] = ['SimHei'] # 用于正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False # 用于正常顯示負號# 創建電影數據集 (用戶評分矩陣)
movies = ['復仇者聯盟', '泰坦尼克號', '盜夢空間', '肖申克的救贖', '阿凡達', '你的名字']
users = ['用戶A', '用戶B', '用戶C', '用戶D', '用戶E']# 創建用戶評分矩陣 (范圍1-5)
ratings = np.array([[5, 3, 4, 5, 2, 1],  # 用戶A[1, 5, 2, 4, 5, 3],  # 用戶B[4, 5, 5, 3, 4, 4],  # 用戶C[2, 4, 3, 5, 1, 2],  # 用戶D[3, 2, 5, 4, 5, 4]   # 用戶E
])# 轉換為DataFrame
ratings_df = pd.DataFrame(ratings, index=users, columns=movies)# 使用KNN查找相似用戶
model = NearestNeighbors(metric='cosine', n_neighbors=2)
model.fit(ratings)# 為"用戶A"尋找相似用戶
userA_ratings = ratings[0].reshape(1, -1)
distances, indices = model.kneighbors(userA_ratings, n_neighbors=3)print(f"與用戶A最相似的用戶:")
similar_users = [users[i] for i in indices[0][1:]]  # 排除自己
print(similar_users)# 基于相似用戶做推薦
similar_users_ratings = ratings[indices[0][1:]]
recommendation_scores = similar_users_ratings.mean(axis=0)
recommendations = np.argsort(recommendation_scores)[::-1]print("\n推薦給用戶A的電影:")
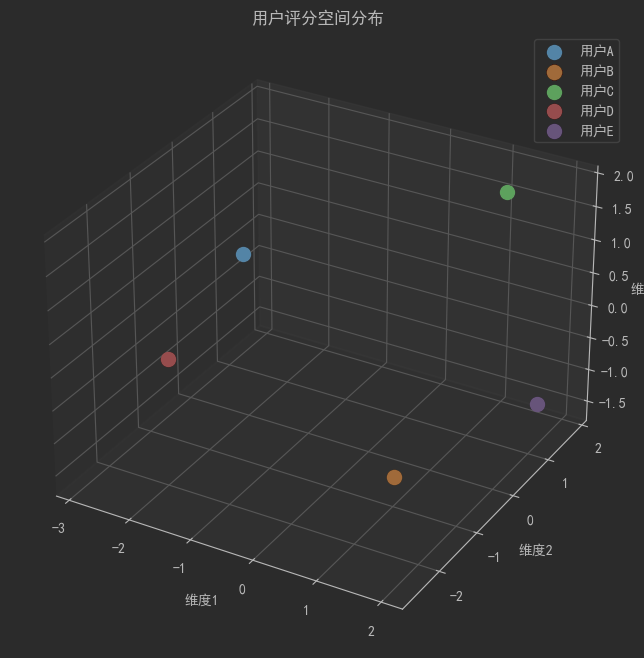
for i in recommendations:if ratings[0, i] == 0:  # 未看過的電影print(f"- {movies[i]} (推薦指數: {recommendation_scores[i]:.2f})")# 3D可視化用戶評分空間
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')# 使用PCA降維到3維進行可視化
pca = PCA(n_components=3)
ratings_3d = pca.fit_transform(ratings)for i, user in enumerate(users):ax.scatter(ratings_3d[i, 0], ratings_3d[i, 1], ratings_3d[i, 2], s=100, label=user)# 添加標簽
ax.set_xlabel('維度1')
ax.set_ylabel('維度2')
ax.set_zlabel('維度3')
ax.set_title('用戶評分空間分布')
plt.legend()
plt.show()

6.2?鳶尾花分類

# 使用scikit-learn完成鳶尾花分類
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier# 加載數據
iris = load_iris()
X, y = iris.data, iris.target# 數據預處理（歸一化）
scaler = StandardScaler()
X = scaler.fit_transform(X)# 劃分訓練集/測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# 創建KNN模型（K=5）
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)# 評估模型
accuracy = knn.score(X_test, y_test)
print(f"準確率: {accuracy:.2f}")  # 輸出: 0.93~0.97

6.3?拓展案例

# 案例拓展
import numpy as np
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap# 生成復雜數據集（同心圓）
X, y = make_classification(n_samples=500, n_features=2, n_redundant=0,n_classes=3, n_clusters_per_class=1,class_sep=0.8, random_state=4)# 可視化決策邊界函數
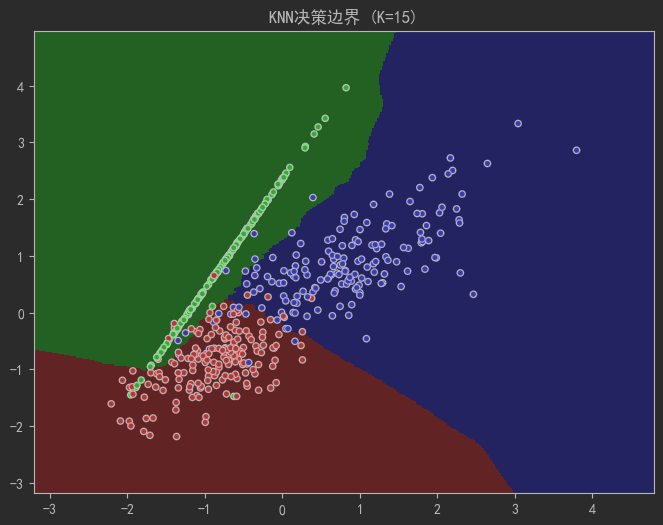
def plot_decision_boundary(k):cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])h = 0.02  # 網格步長# 創建網格x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))# 訓練模型并預測knn = KNeighborsClassifier(n_neighbors=k)knn.fit(X, y)Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# 繪圖plt.figure(figsize=(8, 6))plt.pcolormesh(xx, yy, Z, cmap=cmap_light, shading='auto')plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)plt.xlim(xx.min(), xx.max())plt.ylim(yy.min(), yy.max())plt.title(f"KNN決策邊界 (K={k})")plt.show()# 觀察K值對邊界的影響
plot_decision_boundary(k=1)   # 過擬合：邊界過于復雜
plot_decision_boundary(k=15)  # 欠擬合：邊界過度平滑
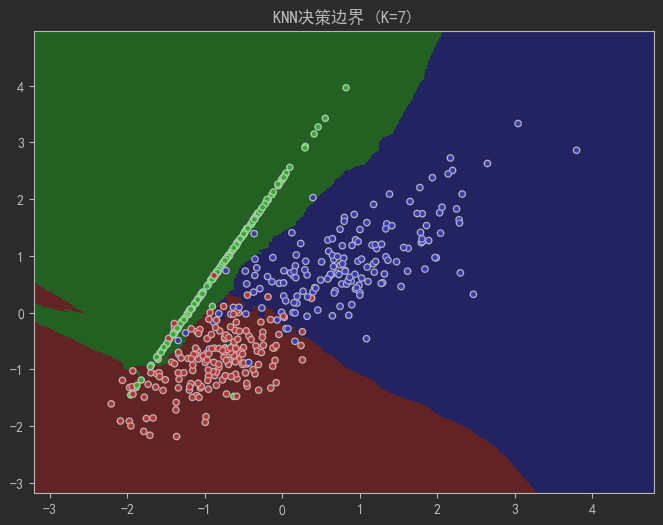
plot_decision_boundary(k=7)   # 最佳平衡點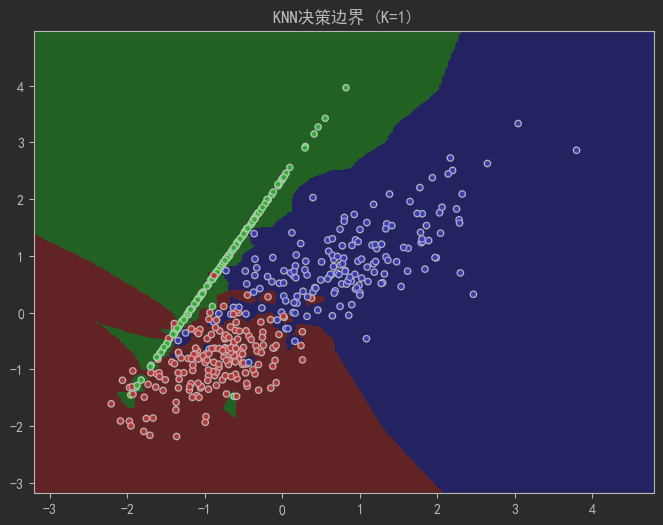

6.4?KD樹加速查詢

# KD樹加速查詢
from sklearn.neighbors import KDTree, KNeighborsClassifier
import numpy as np
import time# 生成測試數據（10000個樣本，10維特征）
np.random.seed(42)
X_train = np.random.rand(10000, 10)
y_train = np.random.randint(0, 3, 10000)# 普通KNN計算
start_time = time.time()
knn_normal = KNeighborsClassifier(n_neighbors=5)
knn_normal.fit(X_train, y_train)
normal_time = time.time() - start_time# KDTree加速的KNN
start_time = time.time()
knn_kd = KNeighborsClassifier(n_neighbors=5,algorithm='kd_tree',  # 使用KD樹算法leaf_size=30  # 葉子節點包含的最小樣本數
)
knn_kd.fit(X_train, y_train)
kd_time = time.time() - start_timeprint(f"普通KNN訓練耗時: {normal_time:.4f}秒")
print(f"KD樹加速后訓練耗時: {kd_time:.4f}秒")
print(f"加速比: {normal_time/kd_time:.1f}倍")# 測試查詢速度
test_sample = np.random.rand(1, 10)start_time = time.time()
knn_normal.predict(test_sample)
normal_pred_time = time.time() - start_timestart_time = time.time()
knn_kd.predict(test_sample)
kd_pred_time = time.time() - start_timeprint(f"\n普通KNN預測耗時: {normal_pred_time:.6f}秒")
print(f"KD樹預測耗時: {kd_pred_time:.6f}秒")
print(f"預測加速比: {normal_pred_time/kd_pred_time:.1f}倍")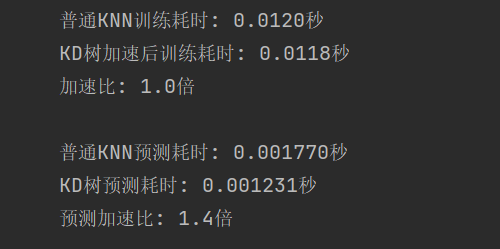

6.5?類別不平衡的加權KNN

# 類別不平衡的加權KNN
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_classification
from sklearn.metrics import classification_report
import numpy as np# 創建不平衡數據集（3類，比例10:2:1）
X, y = make_classification(n_samples=1300, n_classes=3, n_features=4,weights=[0.10, 0.15, 0.75], random_state=42
)# 查看類別分布
print("類別分布:", np.bincount(y))# 1. 普通KNN（未處理不平衡）
knn_normal = KNeighborsClassifier(n_neighbors=5)
knn_normal.fit(X, y)
print("\n[普通KNN分類報告]")
print(classification_report(y, knn_normal.predict(X)))# 2. 距離加權KNN（權重與距離成反比）
knn_weighted = KNeighborsClassifier(n_neighbors=5,weights='distance'  # 距離加權
)
knn_weighted.fit(X, y)
print("\n[距離加權KNN分類報告]")
print(classification_report(y, knn_weighted.predict(X)))# 3. 類別加權KNN + 距離加權
knn_class_weighted = KNeighborsClassifier(n_neighbors=5,weights='distance',class_weight='balanced'  # 類別平衡加權
)
knn_class_weighted.fit(X, y)
print("\n[類別加權+距離加權KNN分類報告]")
print(classification_report(y, knn_class_weighted.predict(X)))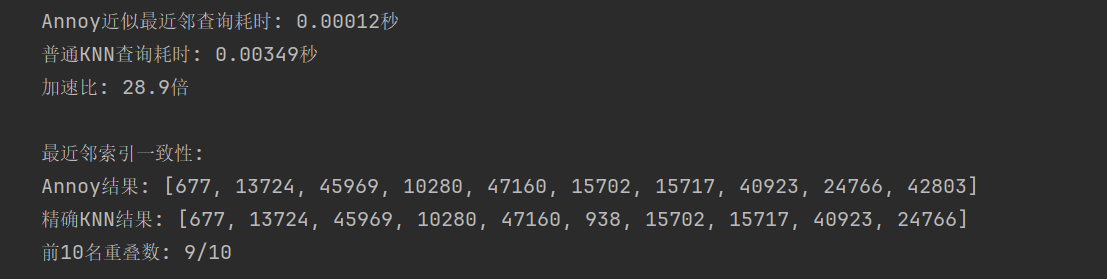

6.6?網格搜索超參數調優

# 網絡優化
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns# 加載并預處理數據
iris = load_iris()
X, y = iris.data, iris.target
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 參數網格配置
param_grid = {'n_neighbors': [3, 5, 7, 9, 11, 13],'weights': ['uniform', 'distance'],'metric': ['euclidean', 'manhattan', 'minkowski'],'p': [1, 2]  # 閔可夫斯基距離的參數
}# 創建GridSearchCV對象
grid_search = GridSearchCV(KNeighborsClassifier(),param_grid,cv=5,  # 5折交叉驗證scoring='accuracy',n_jobs=-1  # 使用所有CPU核心
)# 執行網格搜索
grid_search.fit(X_scaled, y)# 輸出最佳參數
print(f"最佳參數組合: {grid_search.best_params_}")
print(f"最佳交叉驗證準確率: {grid_search.best_score_:.4f}")# 可視化參數性能熱圖
results = pd.DataFrame(grid_search.cv_results_)
top_results = results[results['param_weights'] == grid_search.best_params_['weights']]
pivot_table = top_results.pivot_table(values='mean_test_score',index='param_n_neighbors',columns='param_metric',
)plt.figure(figsize=(10, 6))
sns.heatmap(pivot_table, annot=True, fmt=".3f", cmap="YlGnBu")
plt.title("參數性能熱力圖")
plt.xlabel("距離度量")
plt.ylabel("K值")
plt.show()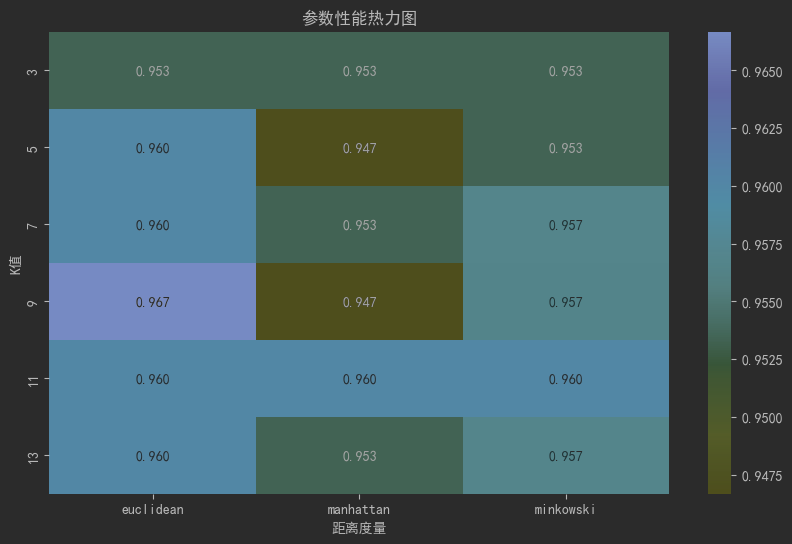

6.7?近似最近鄰(ANN)與維度約減

# 近似最近鄰(ANN)與維度約減
from annoy import AnnoyIndex
from sklearn.decomposition import PCA
import numpy as np
import time# 生成大規模測試數據（5萬樣本，50維）
np.random.seed(42)
X = np.random.randn(50000, 50)# 1. PCA降維 (50維 -> 10維)
pca = PCA(n_components=10)
X_pca = pca.fit_transform(X)# 2. 構建Annoy索引
num_trees = 20  # 構建的樹數量（精度-速度權衡）
annoy_index = AnnoyIndex(X_pca.shape[1], 'euclidean')# 添加所有向量到索引
for i, vec in enumerate(X_pca):annoy_index.add_item(i, vec)# 構建索引
annoy_index.build(num_trees)# 查詢測試
test_vec = np.random.randn(10)
start_time = time.time()# 查找10個最近鄰
indices = annoy_index.get_nns_by_vector(test_vec, n=10)annoy_time = time.time() - start_time
print(f"Annoy近似最近鄰查詢耗時: {annoy_time:.5f}秒")# 對比原始KNN查詢
start_time = time.time()
distances = np.linalg.norm(X_pca - test_vec, axis=1)
sorted_indices = np.argsort(distances)[:10]knn_time = time.time() - start_time
print(f"普通KNN查詢耗時: {knn_time:.5f}秒")
print(f"加速比: {knn_time/annoy_time:.1f}倍")# 檢查結果一致性
print("\n最近鄰索引一致性:")
print("Annoy結果:", indices)
print("精確KNN結果:", sorted_indices.tolist())
print(f"前10名重疊數: {len(set(indices) & set(sorted_indices))}/10")