前言

? ? ? ? 本期我們將學習位運算，與本期類型的考點（二進制轉換）反碼、補碼、原碼。

1、位運算是什么

首先我們需要先了解位運算是什么。

我們知道，計算機中的數在內存中都是以二進制形式進行存儲的?，而位運算就是直接對整數在內存中的二進制位進行操作，因此其執行效率非常高，在程序中盡量使用位運算進行操作，這會大大提高程序的性能。

那么，涉及位運算的運算符如下表所示：

符號	描述	運算規則	實例（以四位二進制數為例）
&	與	兩個位都為1時，結果才為1。	0001&0001=1,0001&0000=0,0000&0000=0000
|	或	兩個位都為0時，結果才為0。	0001∣0001=0001,0001∣0000=0001,0000∣0000=0000
^	異或	兩個位相同為0，相異為1。	0001∧0001=0000,0001∧0000=1,0000∧0000=0
~	取反	0變1，1變0。	～0=1,～1=0
<<	左移	各二進位全部左移若干位，高位丟棄，低位補0。	0001<<k=0100，k=2，k kk是左移的位數，這里k = 2 k=2k=2
>>	右移	各二進位全部右移若干位，對無符號數，高位補0，有符號數，右移補1 11。	0100>>k=0001，k=2，k kk是右移的位數，這里k = 2 k=2k=2

2、位運算的性質

2.1 運算符的優先級

優先級需要弄清楚，如果不太清楚可以加小括號確保是想要的運算順序，這里只是相對優先級，即只是和一些常用的算術運算符做比較。

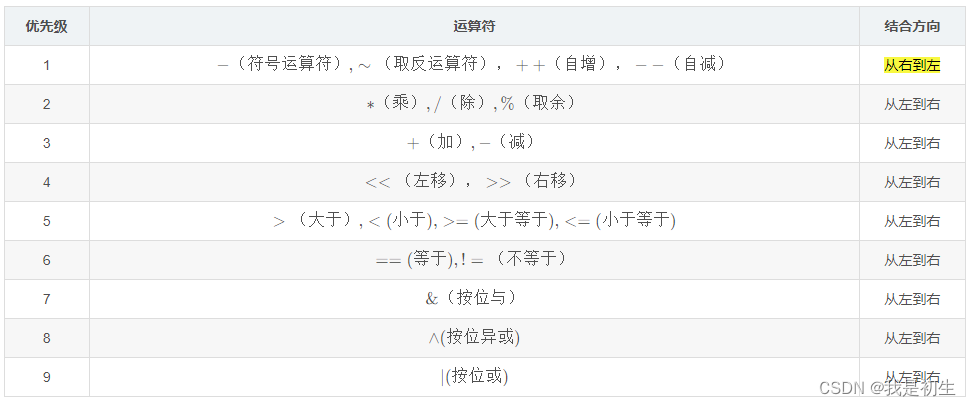
2.2 位運算符的運算律

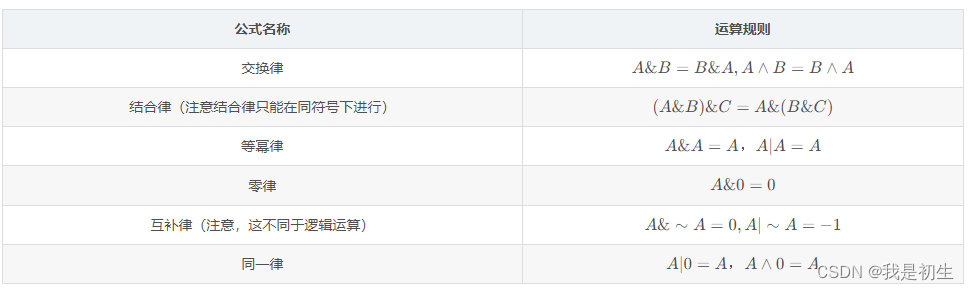
3、位運算高級操作

如下表，請讀者認真閱讀理解，在閱讀的過程中可以對示例進行運算。

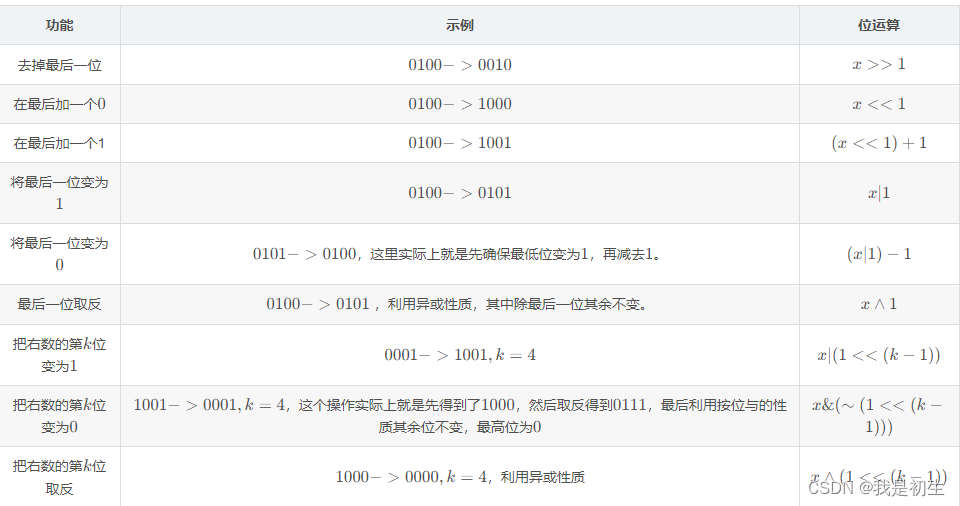
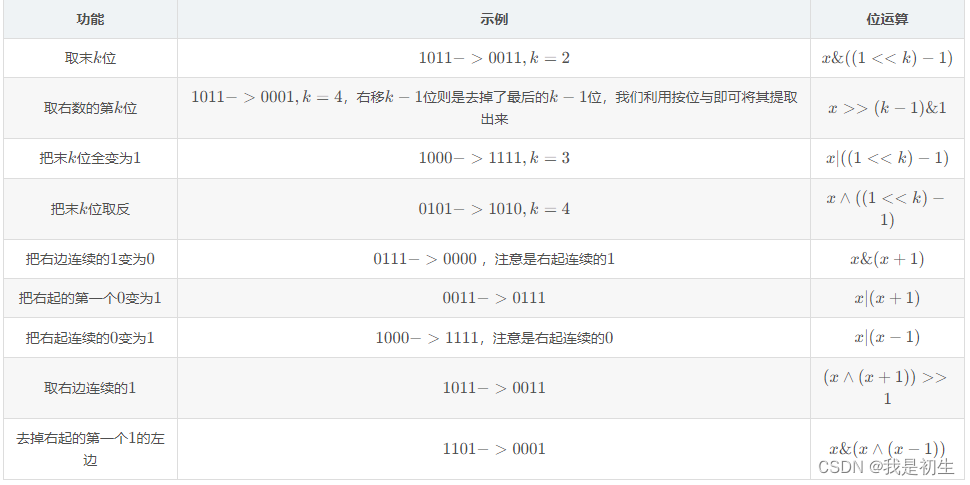
當然，這里只是一些常用的，并不是全部，位運算的神奇遠不止于此。

4、負數的位運算?

首先，我們要知道，在計算機中，運算是使用的二進制補碼，而正數的補碼是它本身，負數的補碼則是符號位不變，其余按位取反，最后再+ 1 +1+1得到的， 例如：

15 1515,原碼:00001111 ? 00001111\space00001111 補碼:00001111 0000111100001111

? 15 -15?15,原碼:10001111 ? 10001111\space10001111 補碼:11110001 1111000111110001

那么對于負數的位運算而言，它們的操作都是建立在補碼上的，得到的運算結果是補碼，最后將補碼結果轉化成一個普通的十進制數結果。
但需要注意的是，對于有符號數的右移操作，不同的處理器架構可能有不同的規定。在某些架構中（如x86），如果對有符號數執行算術右移（arithmetic right shift），則高位空出來的位置會補上符號位；對于無符號數的右移操作，所有架構都遵循相同的規則：高位空出來的位置會補0。例如對于? 15 -15?15，其補碼為11110001 , 11110001,11110001,右移一位( ? 15 > > 1 ) (-15>>1)(?15>>1)得到的是11111000 1111100011111000，即? 8 -8?8，其他的同理。
在大多數現代處理器上，無論是有符號數還是無符號數，左移操作總是將空出來的低位補0。

這里我們介紹幾個特殊的性質：

• 快速判斷是否為-1

????????在鏈式前向星中，我們初始化h e a d headhead數組為? 1 -1?1，最后判斷是否遍歷完u uu的所有邊時，即判斷i ii是否為? 1 -1?1，我們直接用～ i \sim i～i即可。原因就在于? 1 -1?1的補碼是11111111 1111111111111111，按位取反就變為00000000 0000000000000000，這實際上就是0 00。

• 取最低位的1，lowbit函數

????????也就是x & ( ? x ) x\&(-x)x&(?x)，這在樹狀數組中起著巨大作用，這里指路一篇樹狀數組講解b l o g blogblog:點這里，我們來證明一下，這里取x = 15 x=15x=15，對于15 & ( ? 15 ) 15\&(-15)15&(?15)，我們知道，在補碼上進行運算得到的是00000001 0000000100000001，需要注意二元運算的符號位我們需要進行運算。

位運算的運用

1、判斷第i位是否為0

2、將第i位設置為1

3、統計有多少個1?

int count(int x){int cnt = 0;while(x){x = x & (x - 1);cnt ++;}return cnt;
}

對于任意的x xx，轉換成二進制后，是形如這樣的數字：a a . . . a a 10...00 aa...aa10...00aa...aa10...00，從右向左數有任意多個0 00，直到遇見第一個1 11，字母a aa用來占位，代表1 11左邊的任意數字。x ? 1 x-1x?1轉換成二進制后，是形如這樣的數字：a a . . . a a 01...11 aa...aa01...11aa...aa01...11，從右向左數，原來的任意多個0 00都變成1 11，原來的第一個1 11，變成0 00，字母a aa部分不變。對x xx 和 x ? 1 x-1x?1 進行 按位與 計算，會得到：a a . . . a a 00...00 aa...aa00...00aa...aa00...00，從右向左數，原來的第一個1 11變成了0 00，字母a部分不變。所以 x & ( x ? 1 ) x \& (x-1)x&(x?1)相當于消除了 x xx 從右向左數遇到的第一個1 11。那么，x xx轉換成二進制后包含多少個1 11，count函數里的循環就會進行多少次，直到x xx所有的1 11都被“消除”。