• 積分變換常應用于解微分方程

---

微分方程的解法：

• 時域經典法；
• 頻域變換法；

---

“積分變換”最初并不是為了解微分方程，而是出于更“純粹”的數學動機——理解函數的結構、求解代數或幾何問題，以及簡化復雜的積分運算。微分方程的求解，是后來人們意外發現的一個“副作用”，卻最終成了積分變換最重要的應用之一。

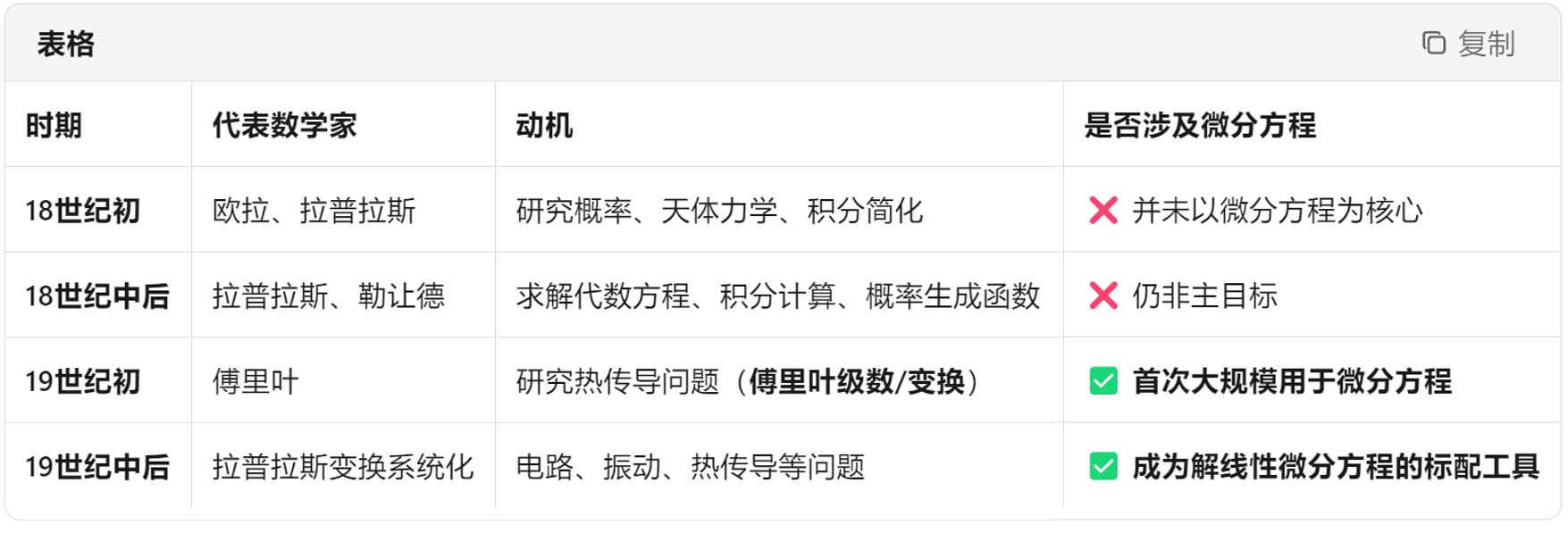
18世紀的時候數學界的一個大熱門方向就是用積分變換來求解微分方程，那時候大家都紛紛推出自己的積分變換。歐拉、拉格朗日、傅里葉、拉普拉斯……

拉普拉斯在1785年推出自己的積分變換公式，但他只是把這個積分變換當作一個求解微分方程的中介轉換，并且他自己也并不清楚這個變化到底表示了什么。

直到在研究了傅里葉變換之后，拉普拉斯才明白了，變換里的S原來是表示復頻率。

由復頻率構成的區域稱為復頻域，也被稱為拉普拉斯域，簡稱拉氏域。

拉普拉斯變換也就是從時域到復頻域的變換。

復頻域可以理解為一個復平面，平面上的每一個點都代表了一個復頻率。

而每個點之上都有一個變化的幅值，所以一個復頻域上的頻譜圖，就成了一個三維立體圖。

而它沿著虛軸的切面，就是傅里葉變換的二維頻譜圖。

傅里葉變換是拉普拉斯變換的一個切片，但是拉普拉斯變化僅在適用范圍更廣，算不上傅里葉變換的升級版，因為這兩個變換聚焦的應用領域不同。

這兩者是在交叉發展的同時，在應用中不斷進化，才在多年后有了形式上的相似與統一。

0. 積分

積分就是函數求和。

實數求積運算：點乘。

函數求積運算：卷積。

求積是求和的拓展，卷積也是以積分的形式進行運算。

1. 傅里葉變換

1.1?角頻率

頻率

• 概念：每秒鐘完成動作的次數。
• 單位：赫茲，Hz。

角頻率

• 概念：每秒鐘“轉圈動作，角度變化”的頻率。
• 單位：弧度/秒，rad/s

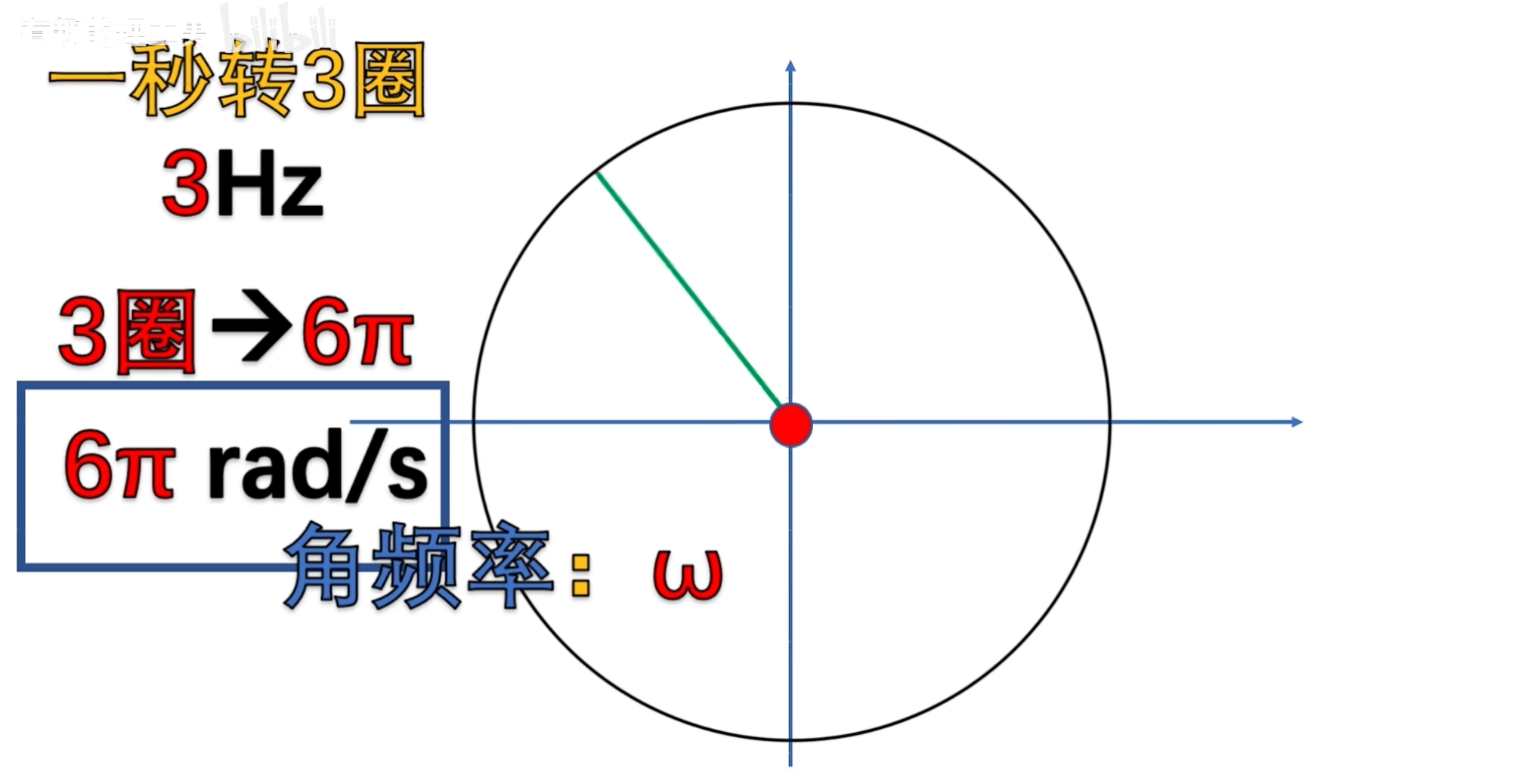
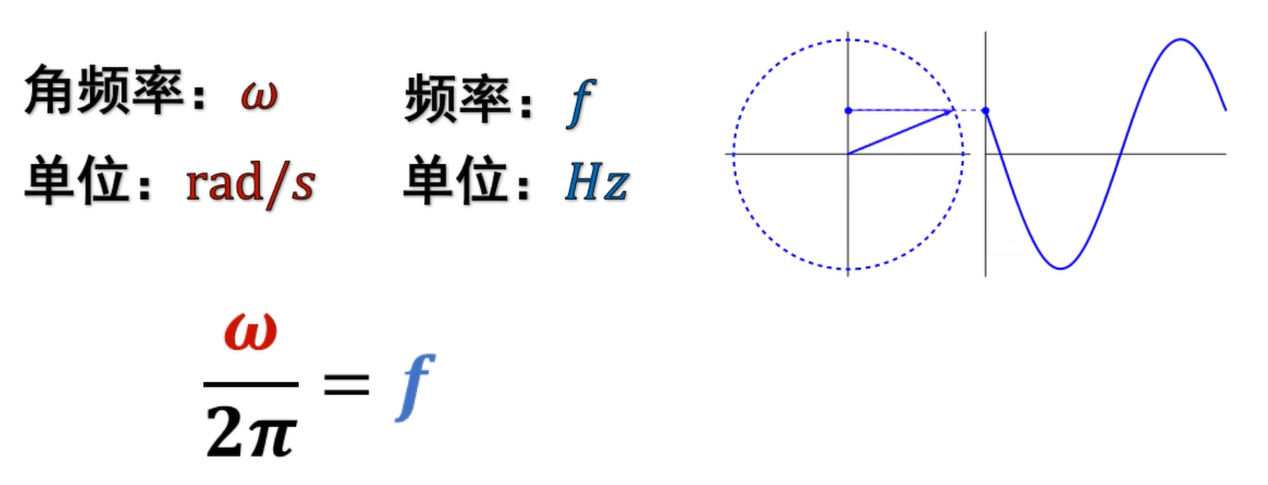
角頻率與正弦函數

正弦函數在直角三角形中的定義是：直角邊與斜邊的比值。

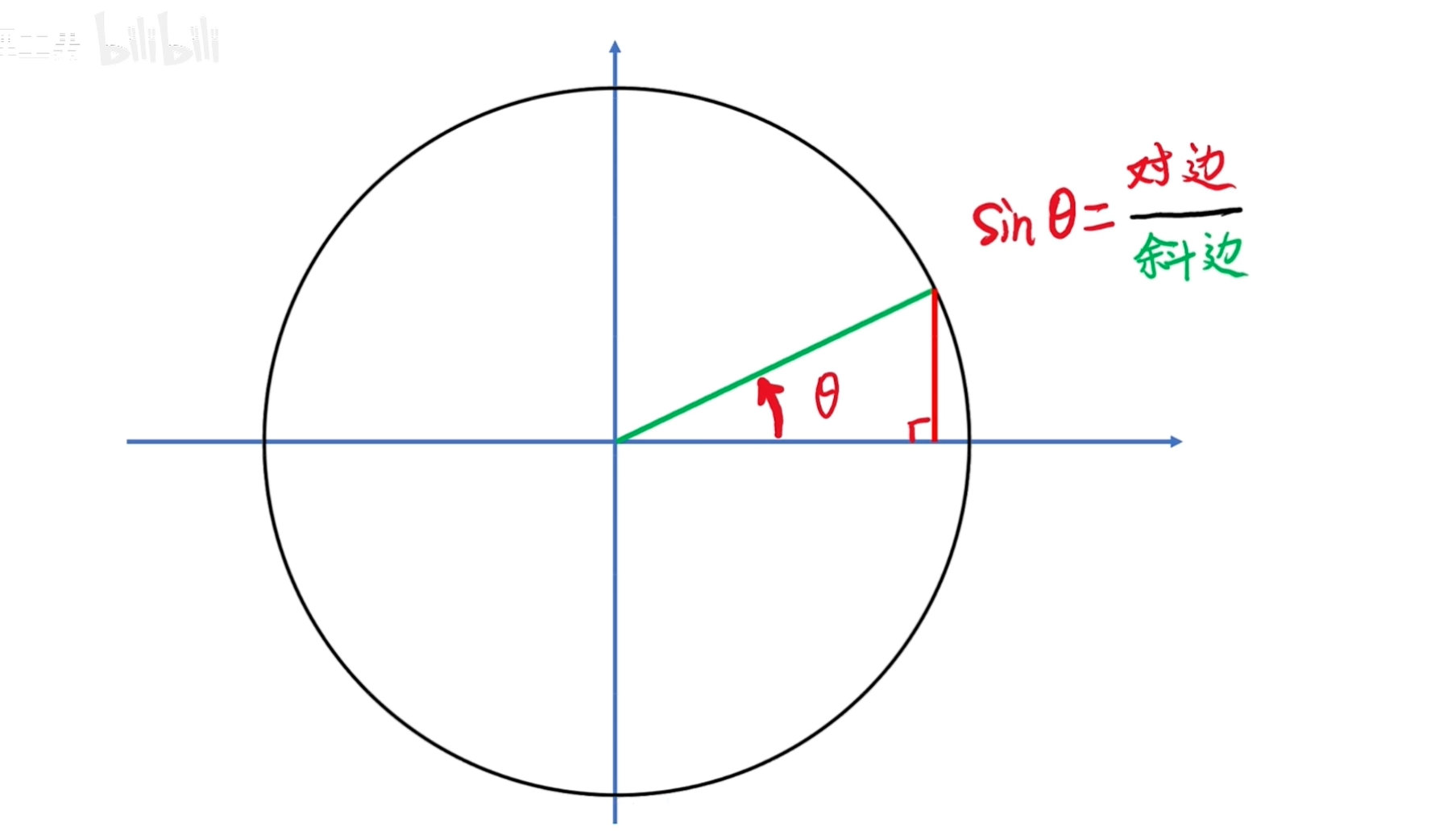
這個夾角的正弦值就是紅邊與綠邊的比值。

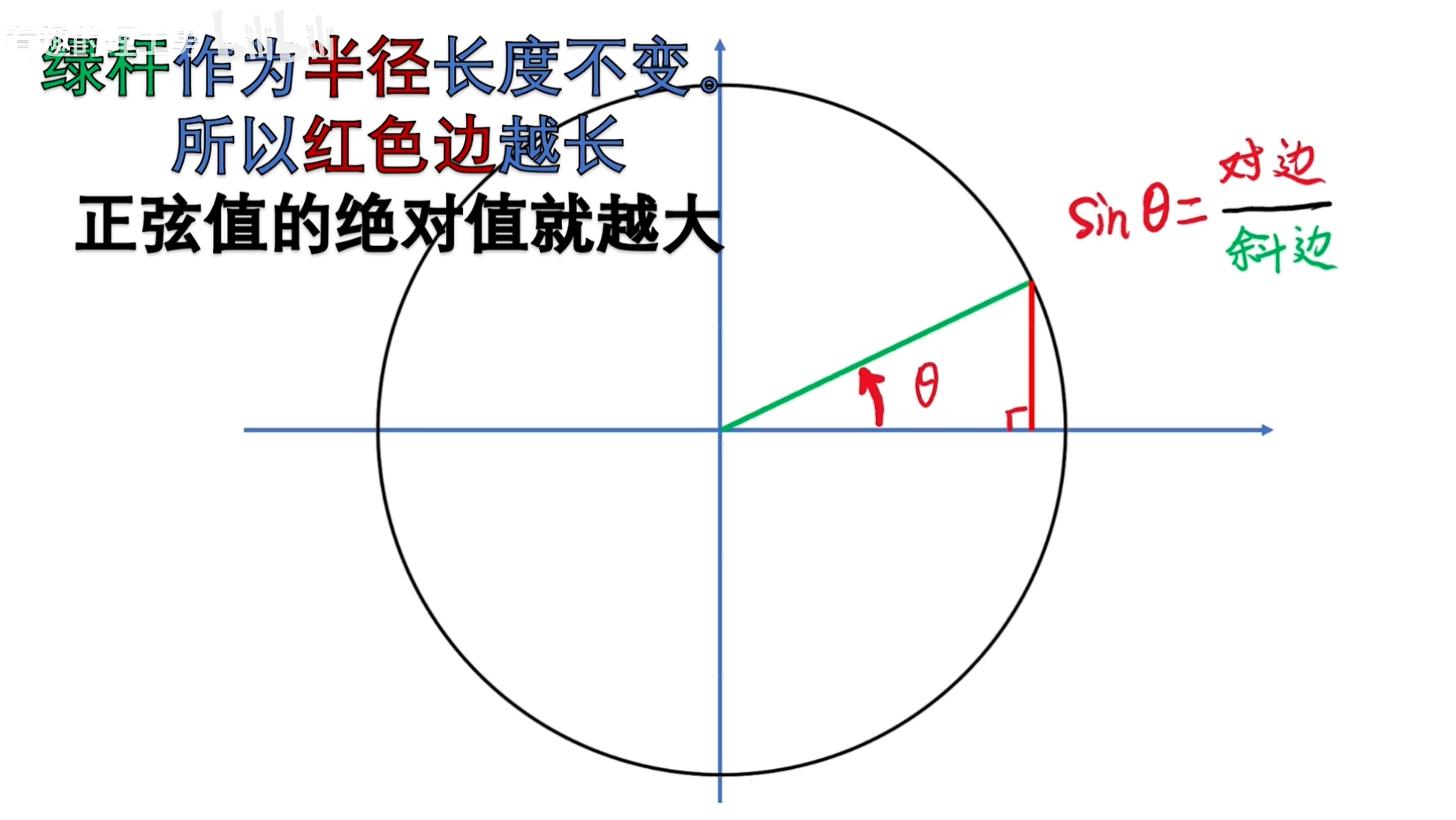
變化的角度可以用角頻率乘以時間來表示：θ = ωt。

所以正弦值可以轉換表示為：sinθ = sin(ωt)。

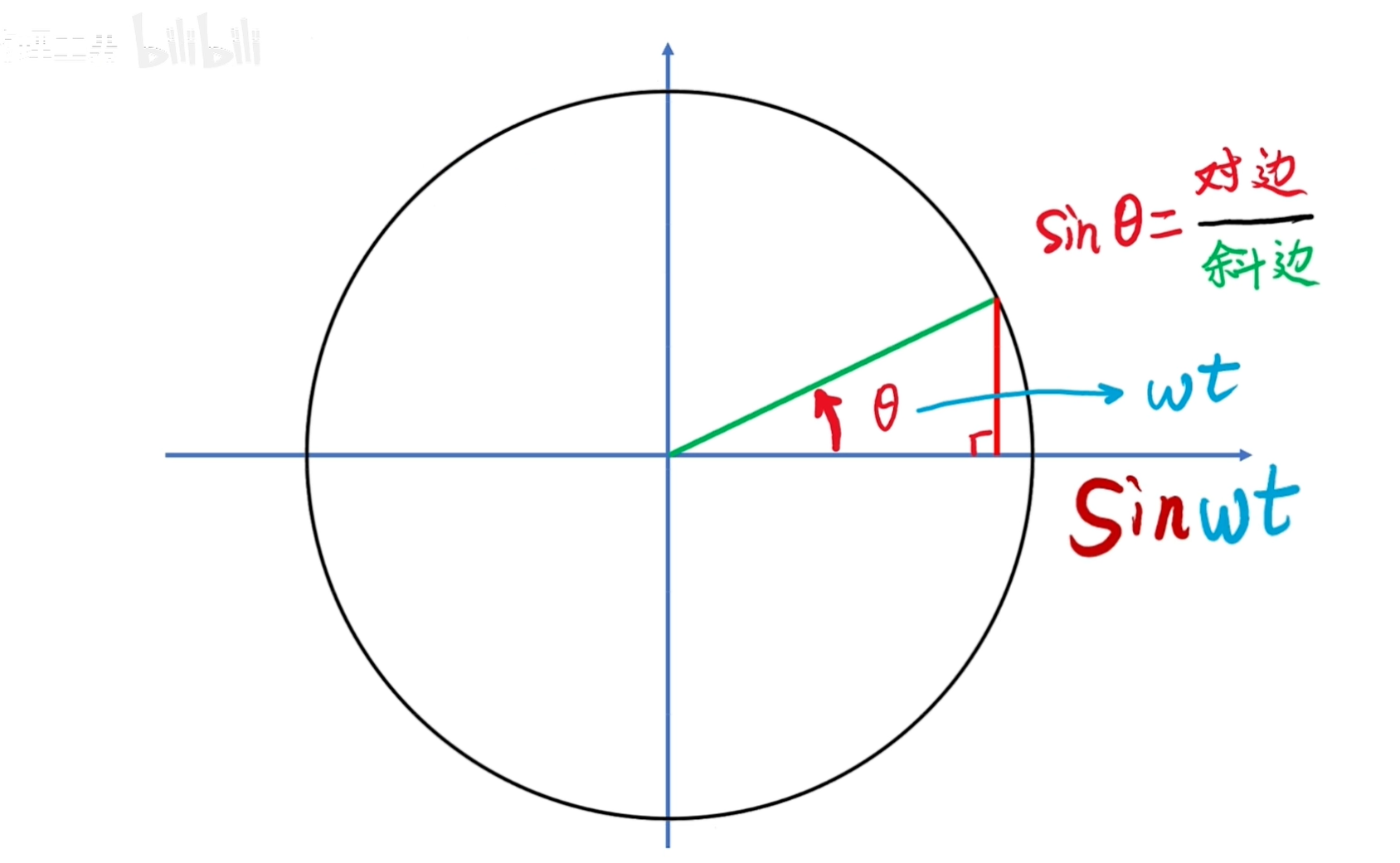
表示正弦值是時間的函數。

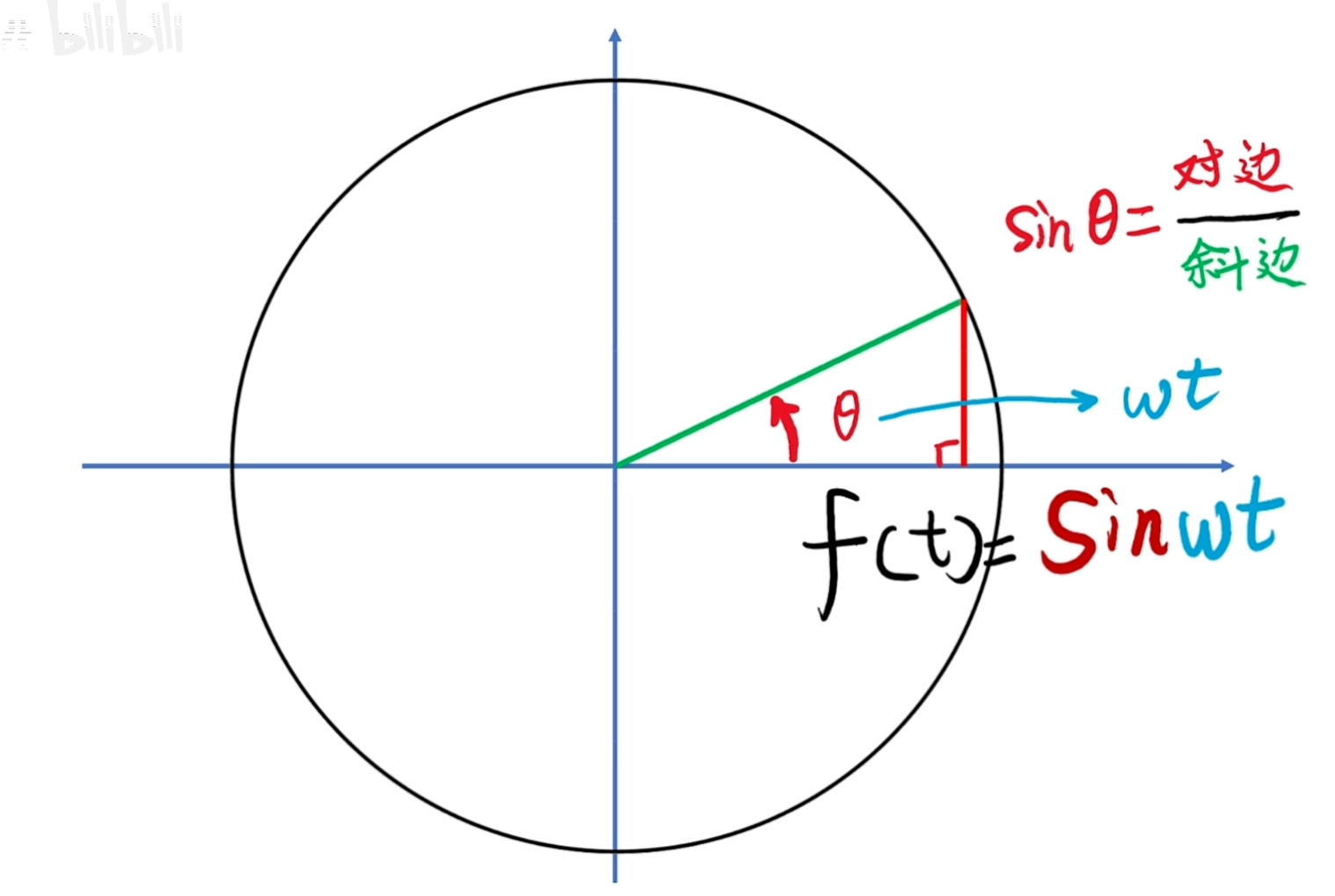
把轉圈的動作加上一條時間軸，讓旋轉的動作沿時間的方向前進，它就形成了一個立體的螺旋形狀。

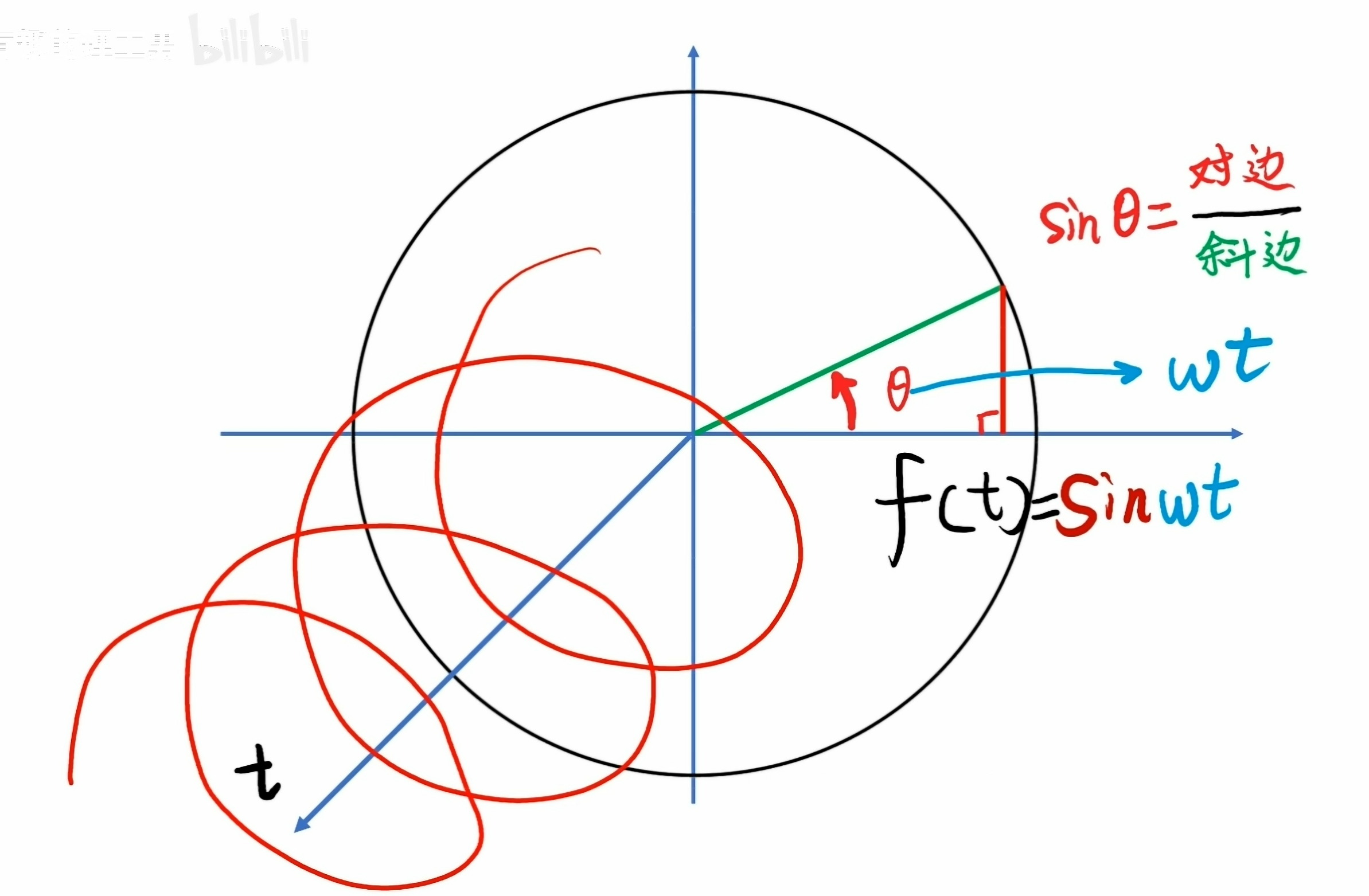
就像拉開的彈簧一樣。從正面看過去它還是一個圓圈，它在那里轉。

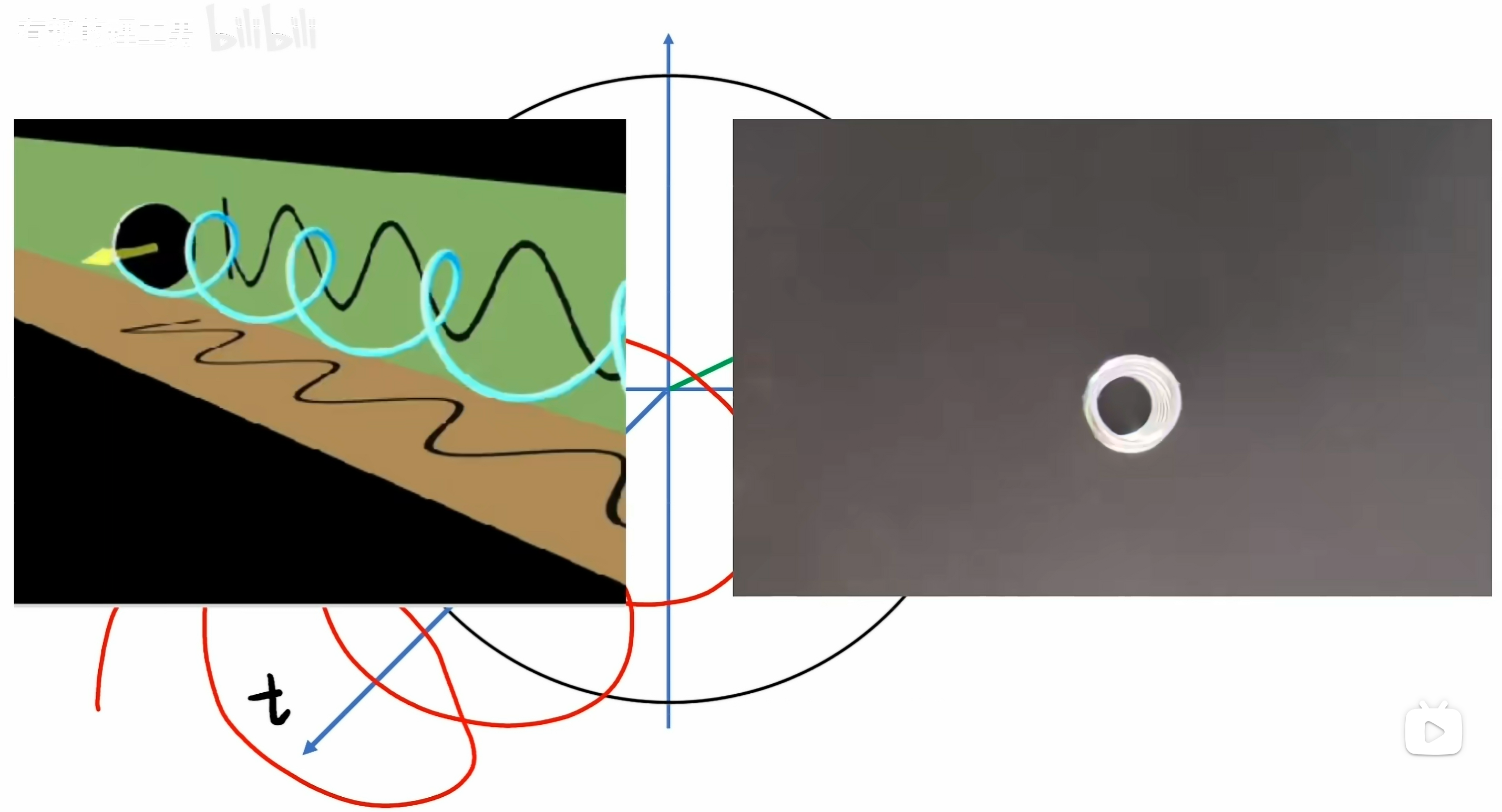
從側面看，即把時間軸展開了，就看到了一個正弦波形。

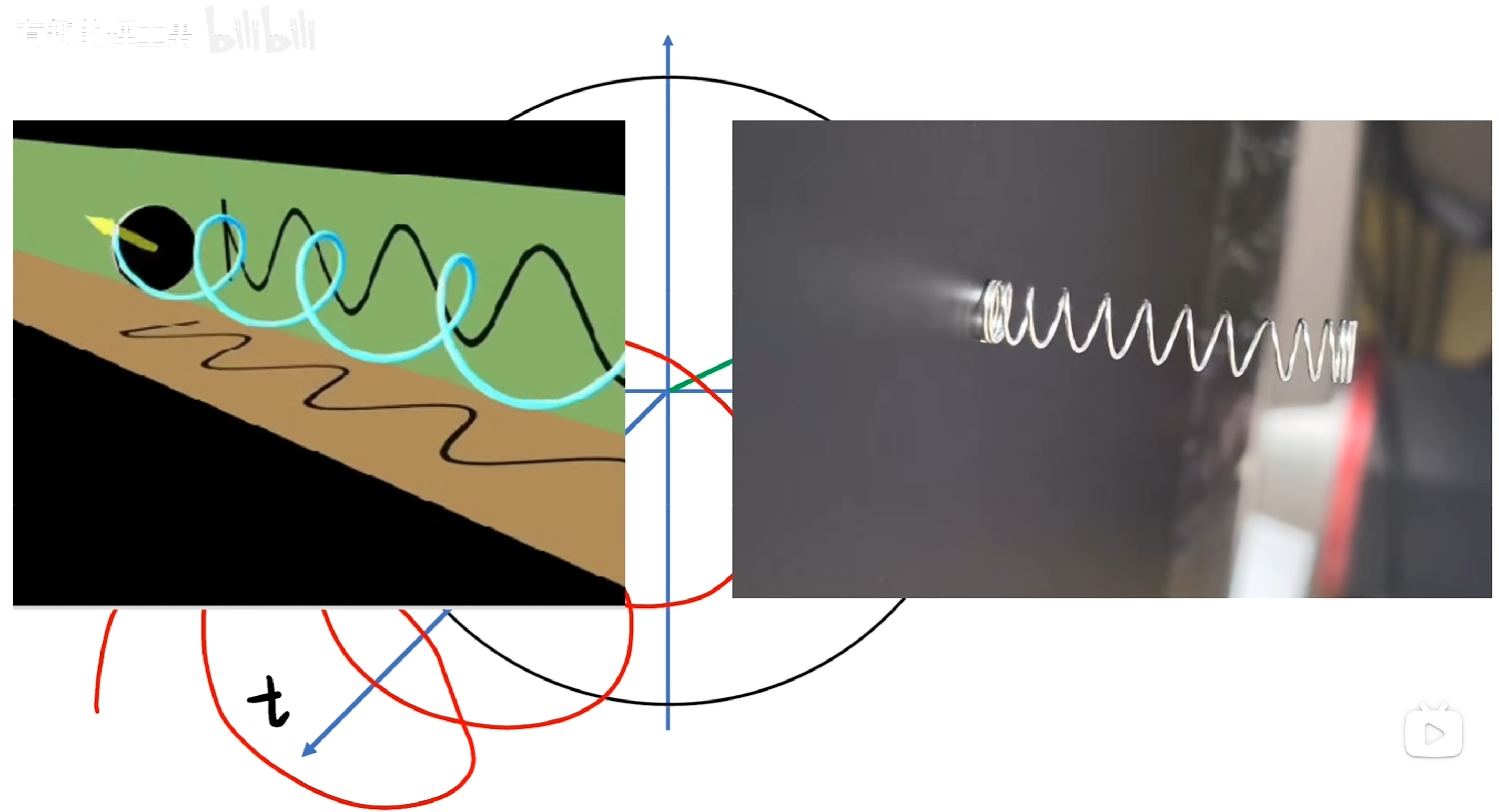
當這個角頻率越大，也就是旋轉得越快的時候，從側面看的正弦波形就更緊湊。

傅里葉級數就是把一個復雜信號分解成很多個正弦信號的疊加：

區分這些正弦波形的最明顯的特征就是——角頻率：ω。

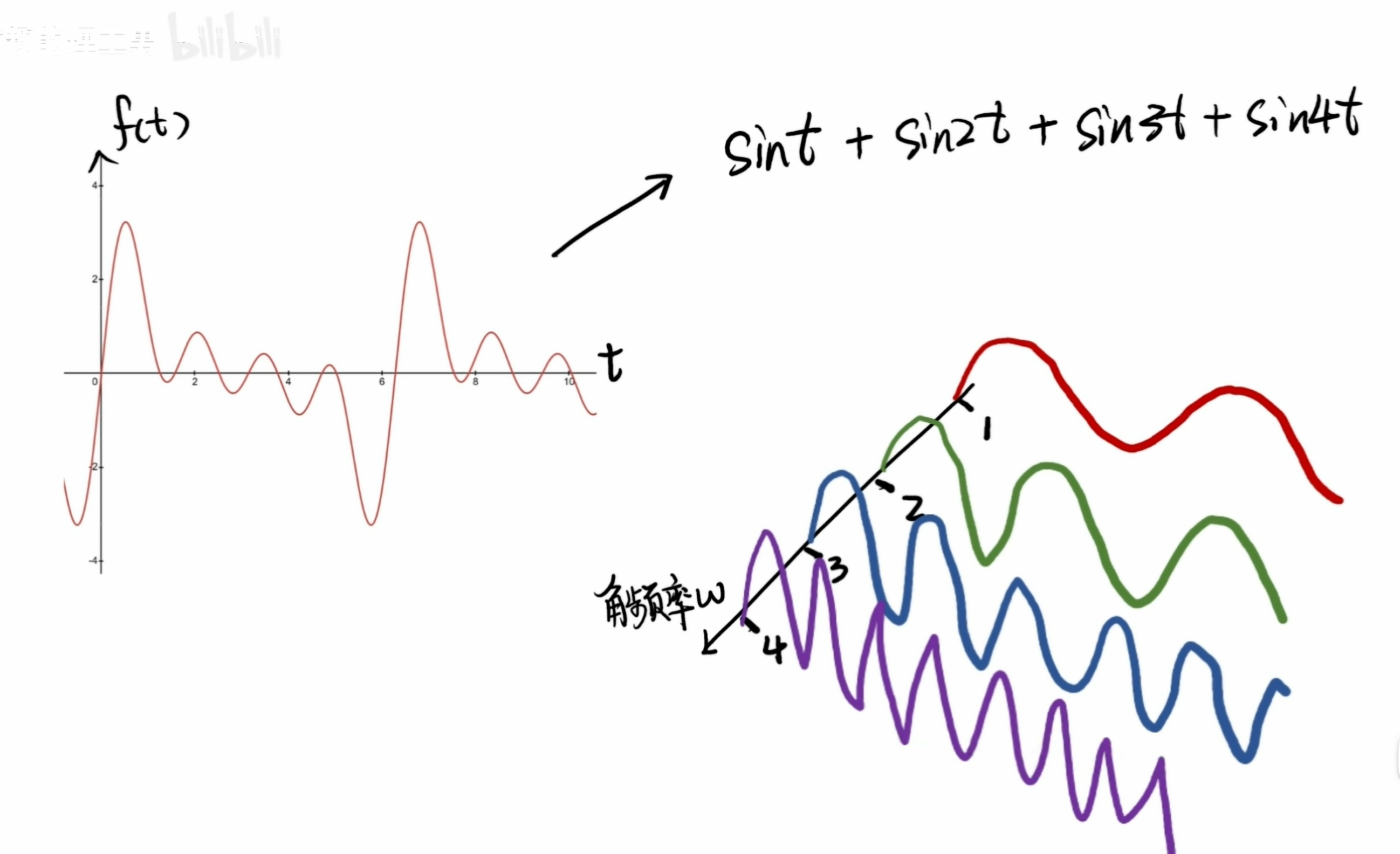
已知復雜信號f(t)可以拆分成上述的三角函數組合，那么就可以建立一條角頻率的軸，然后再按這個順序把這些正弦波形給放置好。——這其實就是傅里葉變換里的頻域，即取頻率為自變量對信號進行分析。

1.2?傅里葉變換簡介

以信號分析為例，下面是紅綠黃交通信號燈：

不同顏色的信號的頻率是不一樣的。

若是交通燈的規律是：紅8秒、黃3秒、綠10秒。

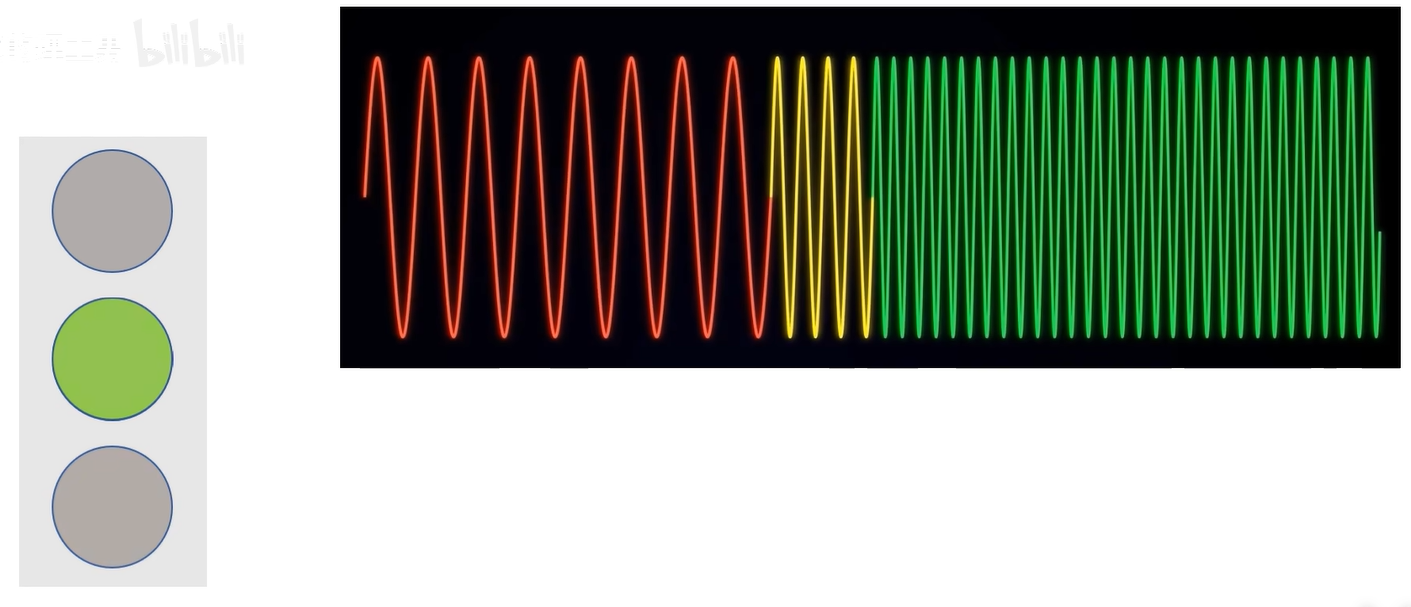
那就可以在坐標軸上繪制出來，得到一個隨時間變化而變化的信號函數。這就是信號的時域表達。

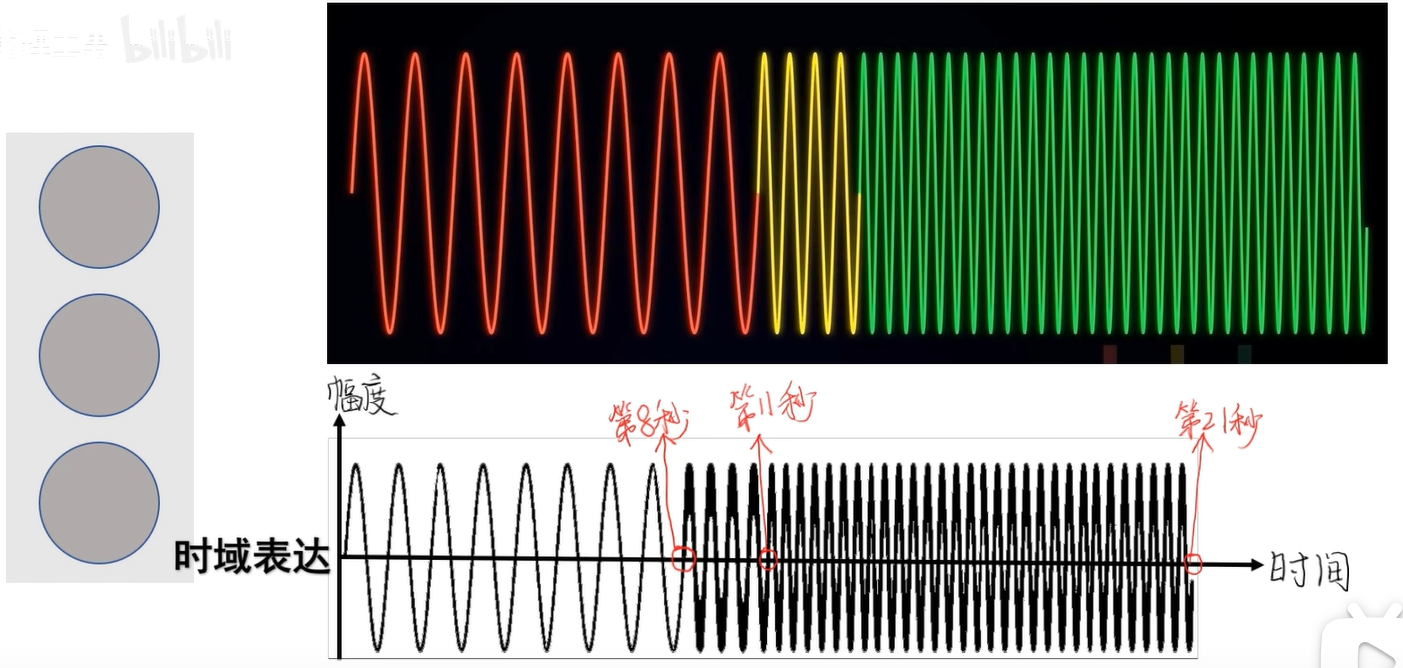
燈壞了，三個燈同時亮，這些信號在時間上有重疊，波形就會疊加，用時域的表達就會很看起來很混亂，也看不出有哪些頻率成分。

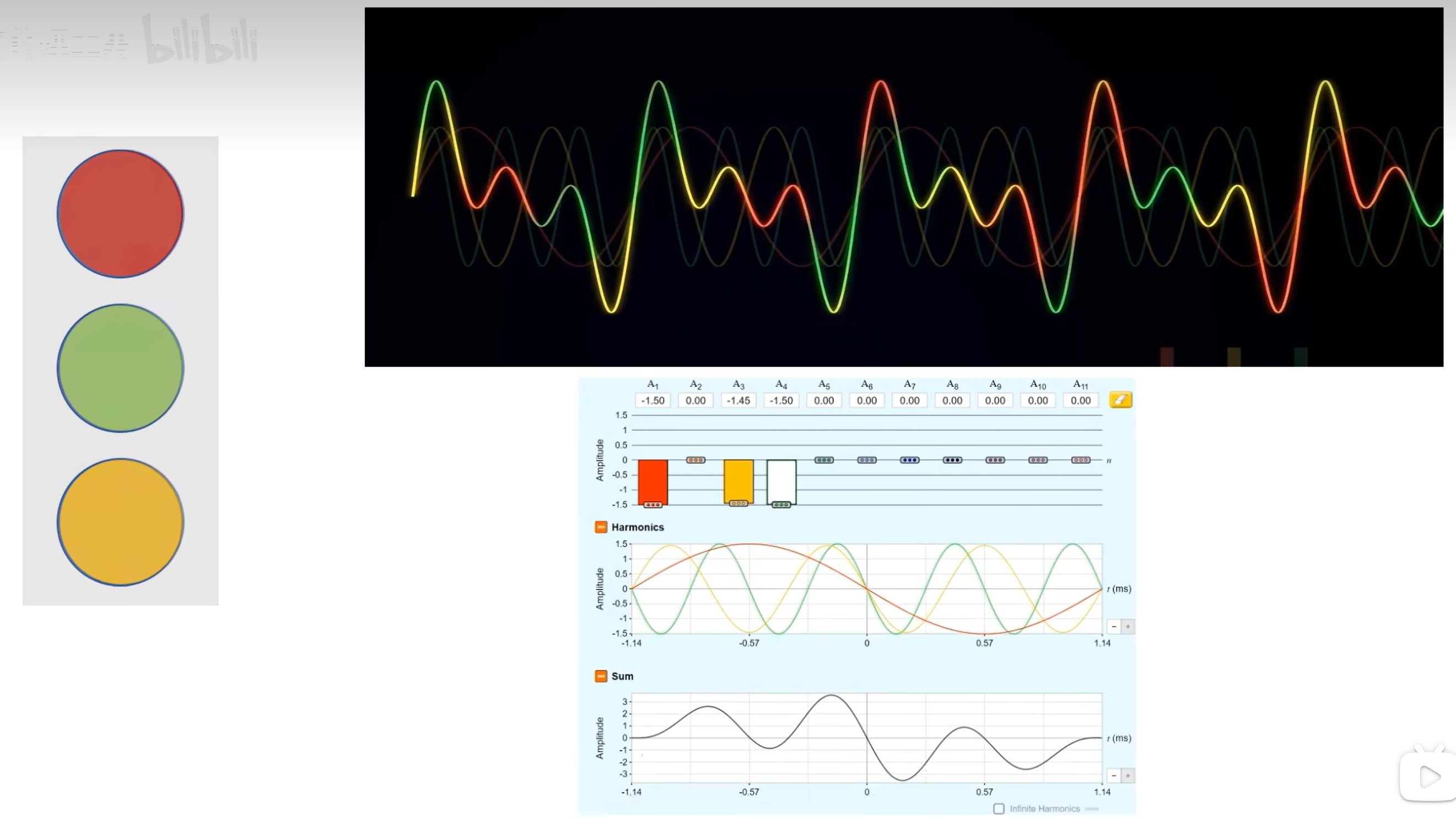
傅里葉變換可以讓我們把這些混疊在一起的信號分拆開，讓我們知道這個信號是由哪些頻率成分構成的。

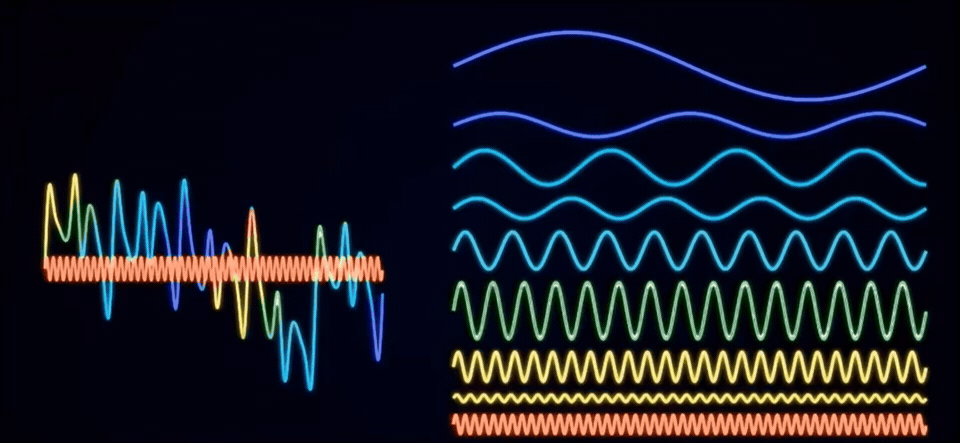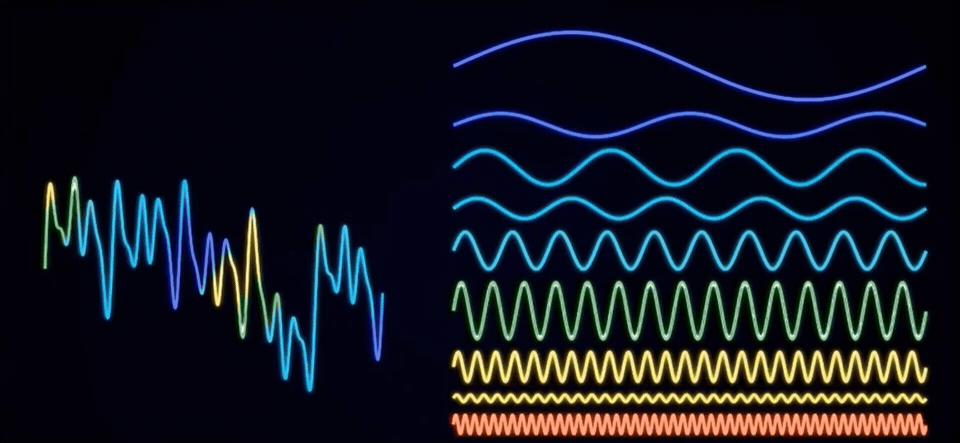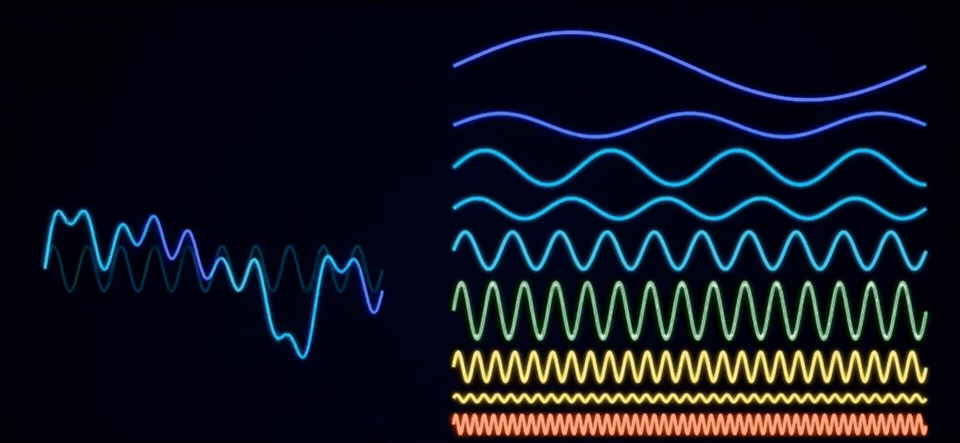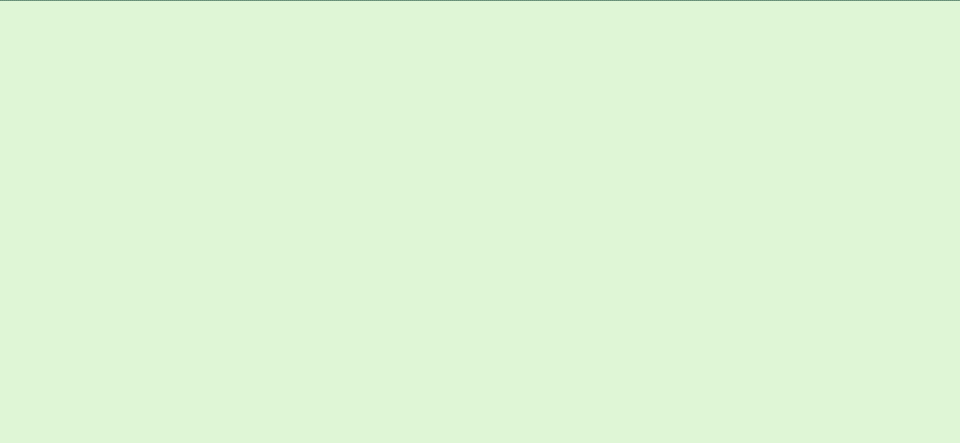
例如剛才的信號經過傅里葉變換之后就成了這樣，從側面看拆分后的頻率投影，其實就是頻域圖。

（幅頻圖）

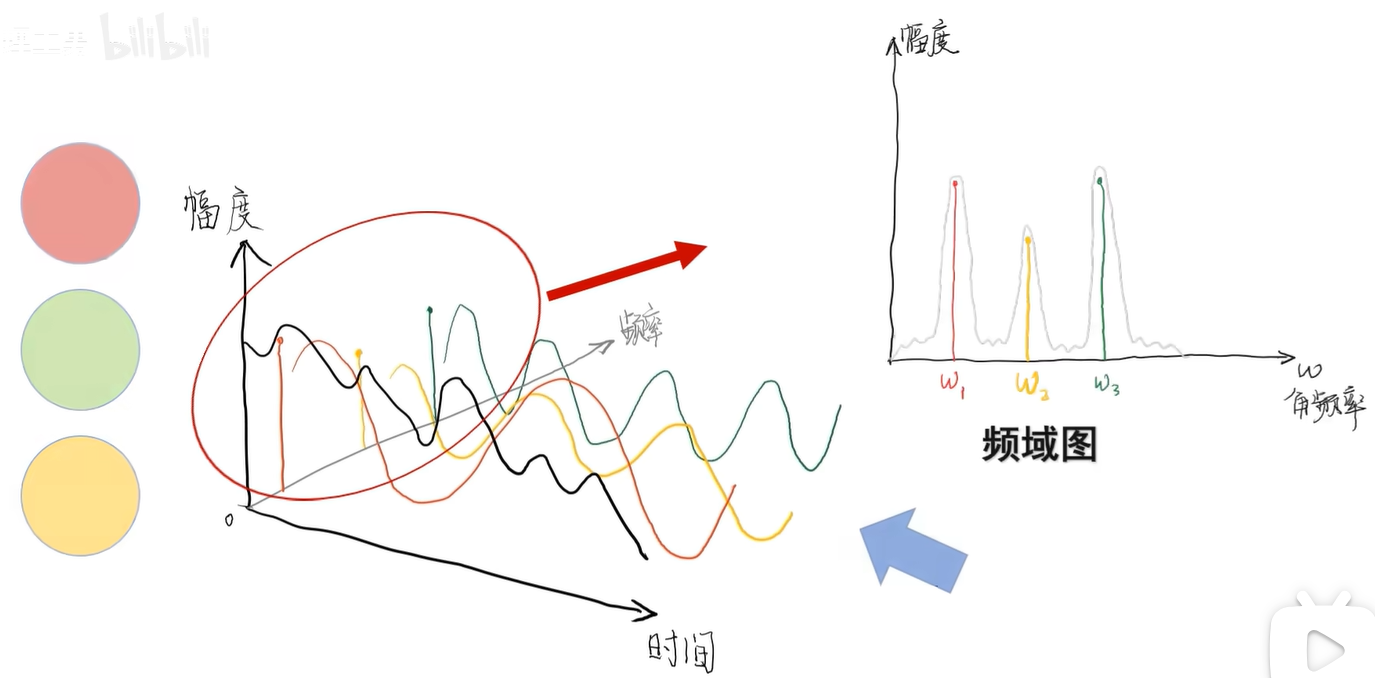
引入頻率信息的代價是犧牲掉時間信息，可以用小波變換取時域、頻域的平衡。

頻域圖的橫坐標是角頻率：

這個圖的ω1、ω2、ω3位置有3條豎線，分別代表紅、黃、綠三個信號，高度代表強度，即振幅。

這是關于角頻率的函數，故而也把變換后的信號稱作頻域的信號。

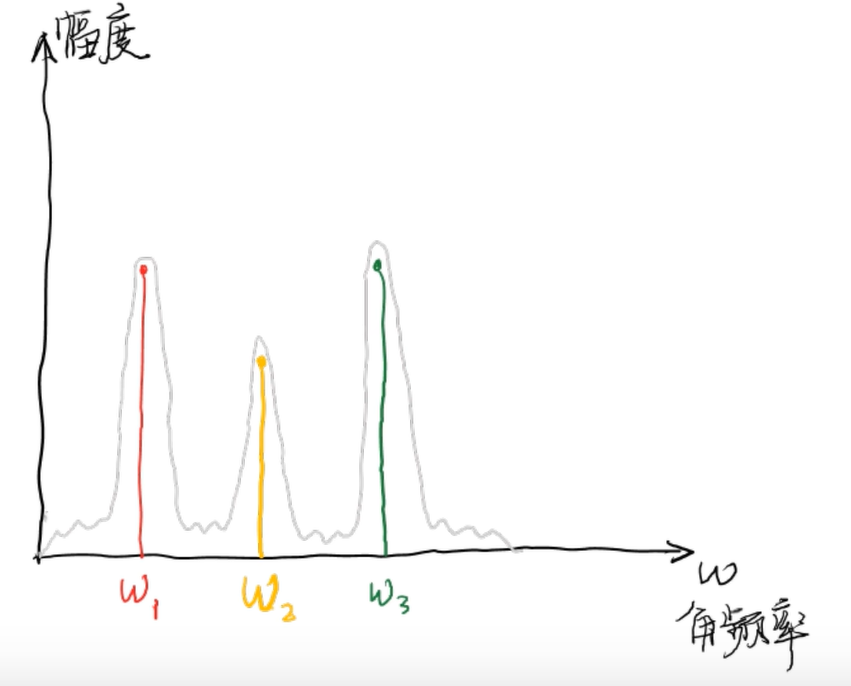
傅里葉變換能夠幫助我們完成從時域到頻域的轉換，但是傅里葉變換也有局限性。

1.3?傅里葉變換的不確定性原理

頻域圖看不出時間的變化，因為從側面看它就是一條線。

以信號燈為例，無論信號燈以何種組合形式來閃動，頻域圖是不變的。

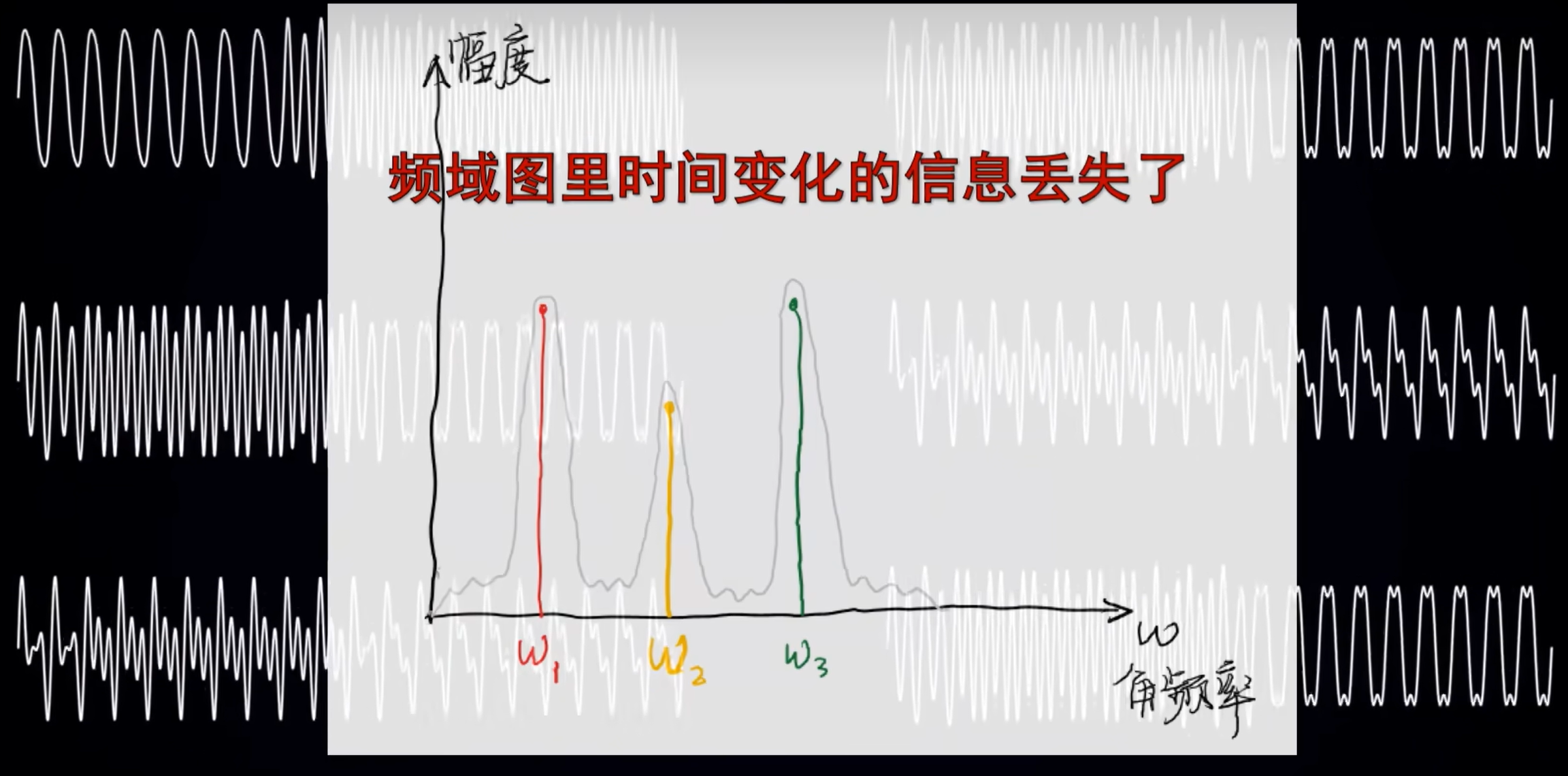
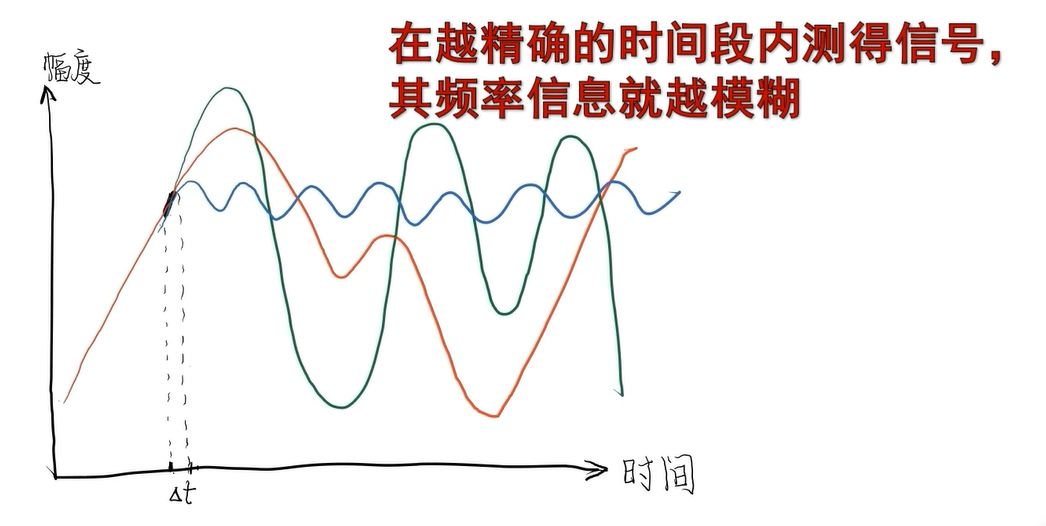
同樣，在越精確（越窄）的一段時間內得到一段精確信號，在頻率上能得到的信息就越模糊。

——傅里葉變化的不確定性原理。

理解：頻率指的是一秒內完成幾個周期循環，不給信號時間讓它振完一個周期，頻率就只能靠估了。

類似于量子力學領域海森堡的不確定性原理：微觀粒子的位置和動量不能同時準確地獲得。

從數學上看，這些不確定性原理（測不準原理）是一回事——是事物本身的性質，和測量工具的精度無關。

1.4?傅里葉變換的由來

1.4.1?傅里葉級數的起源

19世紀法國天才數學家、物理學家傅里葉在他的著作《熱的解析理論》一書中提出：任何周期函數都可以分解成一個三角級數。

傅里葉在研究固體熱傳導的時候，提出了傅里葉級數的雛形……

2?拉普拉斯變換

發散函數不太好求傅里葉變換，可以先乘上一個收斂函數e^-ax，再求傅里葉變換。

拉普拉斯變化的公式，可以看到和點乘的積分形式特別相似：

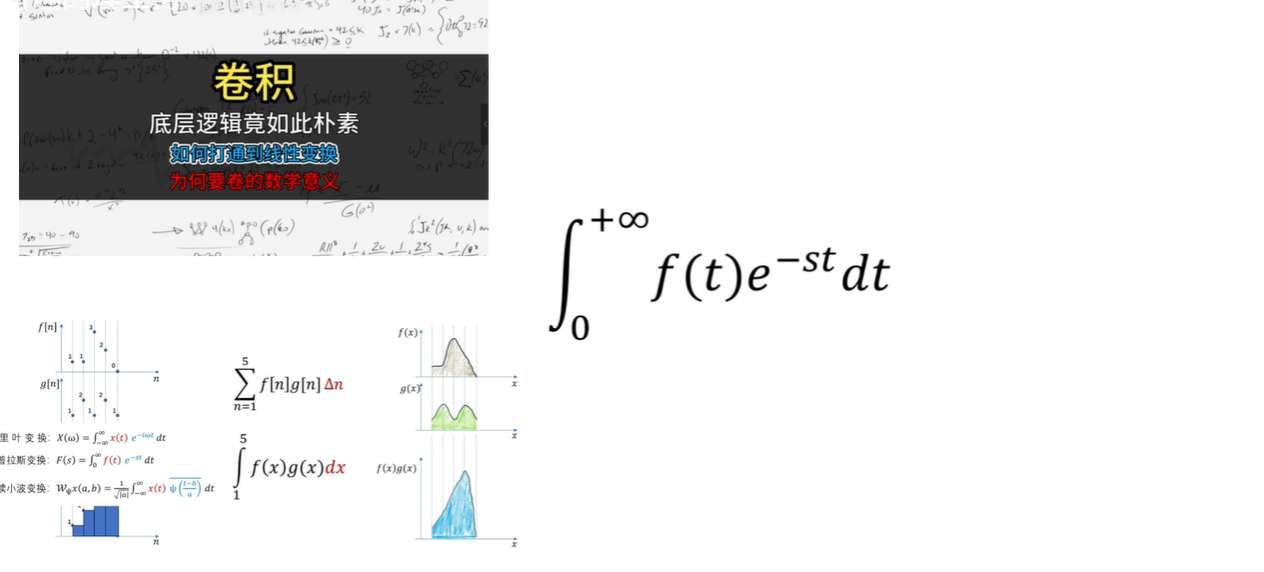
拉普拉斯的底層原理也是點乘：

• 我們使用一個東西去與目標函數進行點乘，目的就是想方設法去把這個目標函數的信息給榨取出來。

2.1?拉普拉斯變換想從原函數中榨取什么信息

我們這個世界遵循熵增法則，世界萬物的有序度一定是在衰減的，所有的自然事物都會在時間的流逝中慢慢消磨自己。

這些現象都對應到一個詞——衰減。

所以研究衰減的規律，就很重要了。

學傅里葉變換時知道，一條復雜的函數曲線可以分解成無數個不同頻率的簡單正余弦函數的線性疊加。

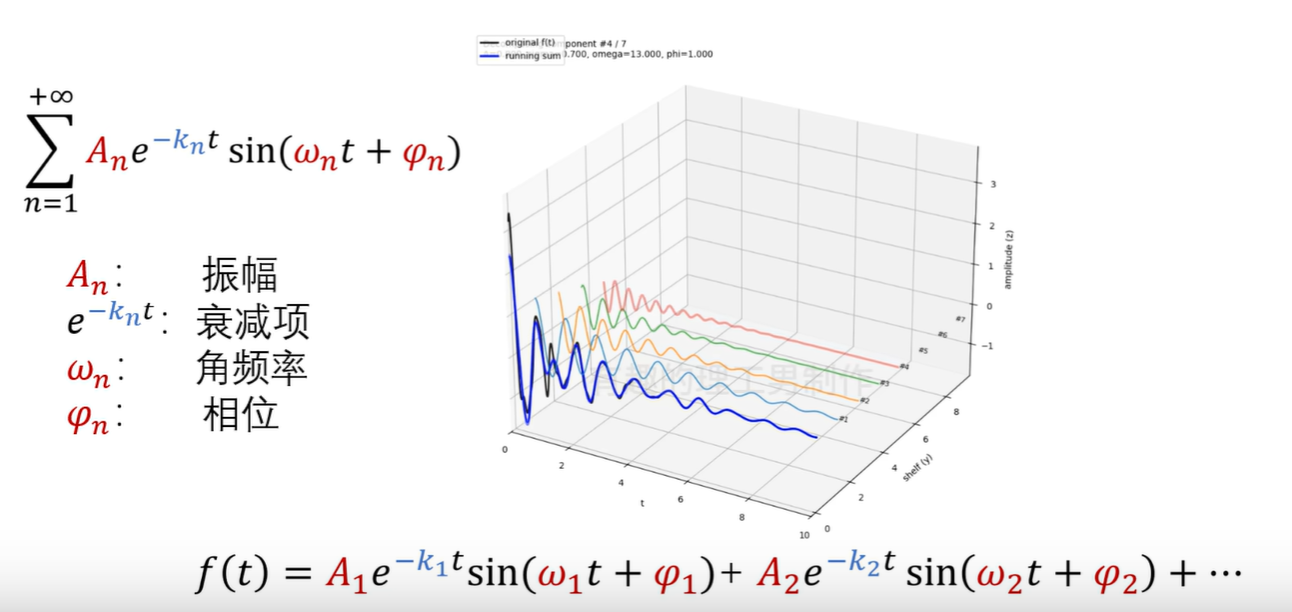
以上是一條衰減曲線，分解成不同成分帶著不同程度的衰減的正弦函數的線性組合，有些頻率成分衰減得慢、有些頻率成分衰減得快。

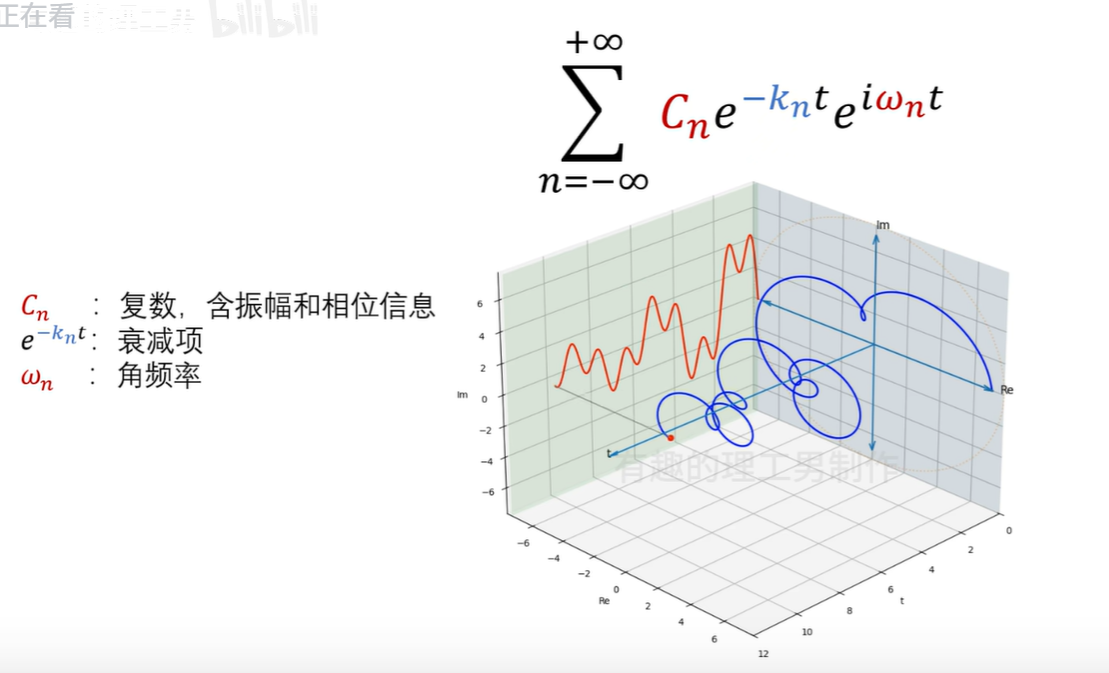
至此我們得知描述衰減現象有兩個最重要的參數：頻率ωn、衰減系數-kn。

如何利用拉普拉斯變換榨取出：頻率ωn、衰減系數-kn這兩個信息呢？？？

---

回顧傅里葉變換

帶入每個ω，就可以得到每個頻率下振蕩的振幅，即每個頻率的振蕩強度（正比于A^2）。

而且這個復函數包含相位信息，即每個頻率下的振蕩是從什么時候開始的也知道了。

---

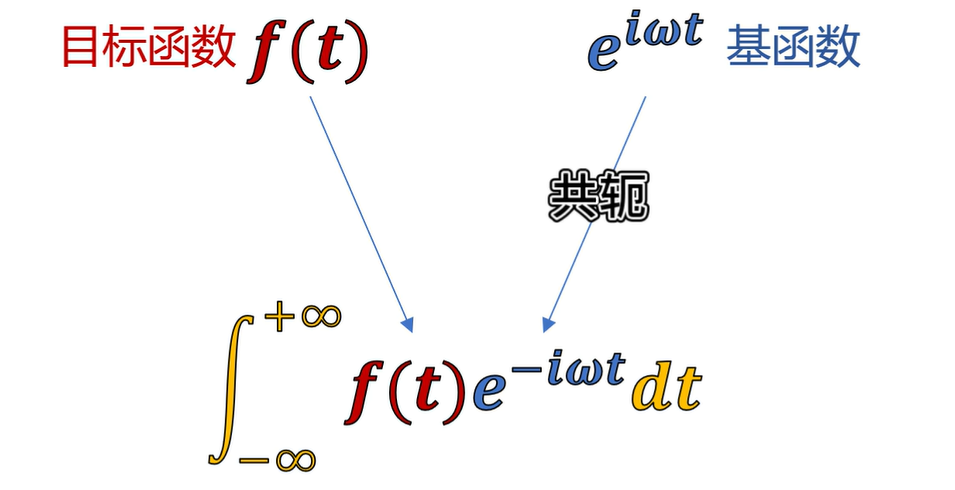
在復數域，和另一個函數點乘，應該是使用自己的共軛去和別人相乘，再求積分。

---

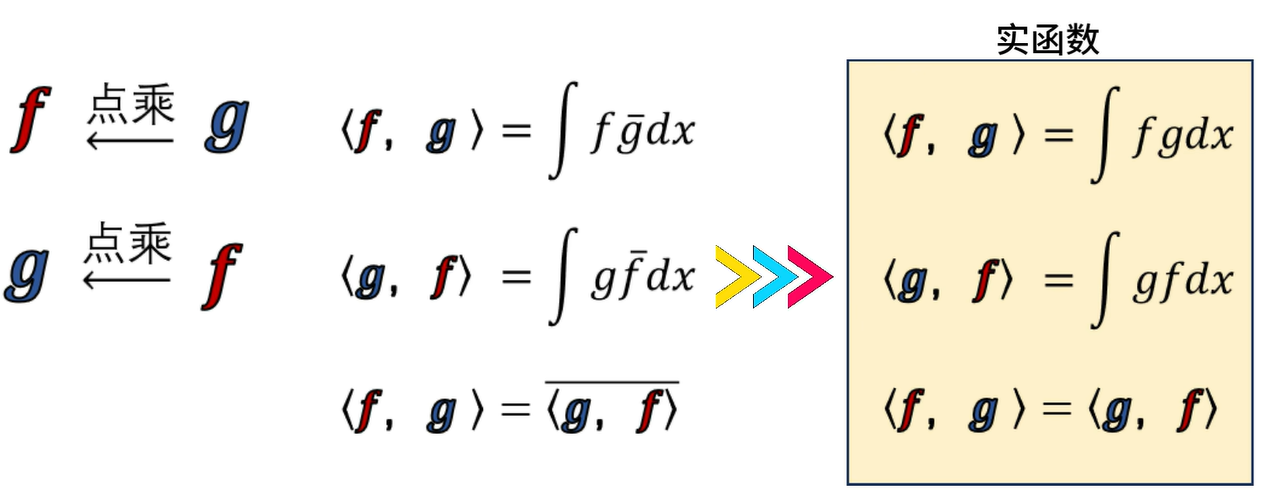
想得到衰減函數（振幅衰減，中心頻率不變）也還是可以使用e^iωt這個基去點乘得到

但是這樣得到的頻率信息，和傅里葉變換還是有很大的差別，因為傅里葉變換可以得到這個頻率下的能力占比，但是現在拉普拉斯點乘得到的東西還會受制于衰減系數，衰減地快一些，能量就會低一些。

所以還是需要找到衰減系數——方法：做標記。

衰減的形象可以描述為一個本不收斂的函數被另一個衰減的函數給摁了下去，如果想辦法把這個衰減的函數的干掉，剩下一個發散的函數積分——標記極點。

用傅里葉變換的手段，搭配抵消衰減的指數函數，取獲取頻率和衰減的信息。

當衰減剛好抵消，且頻率完全共振的時候，積分值無窮大，而其他位置就收斂。那么只要找到無窮大的地方，看一下它抵消衰減的衰減系數以及頻率，那我們要研究衰減現象最重要的兩個東西就知道了。

那就有：

那我們盯著無限大的地方，就可以找到對應的衰減系數和頻率了。

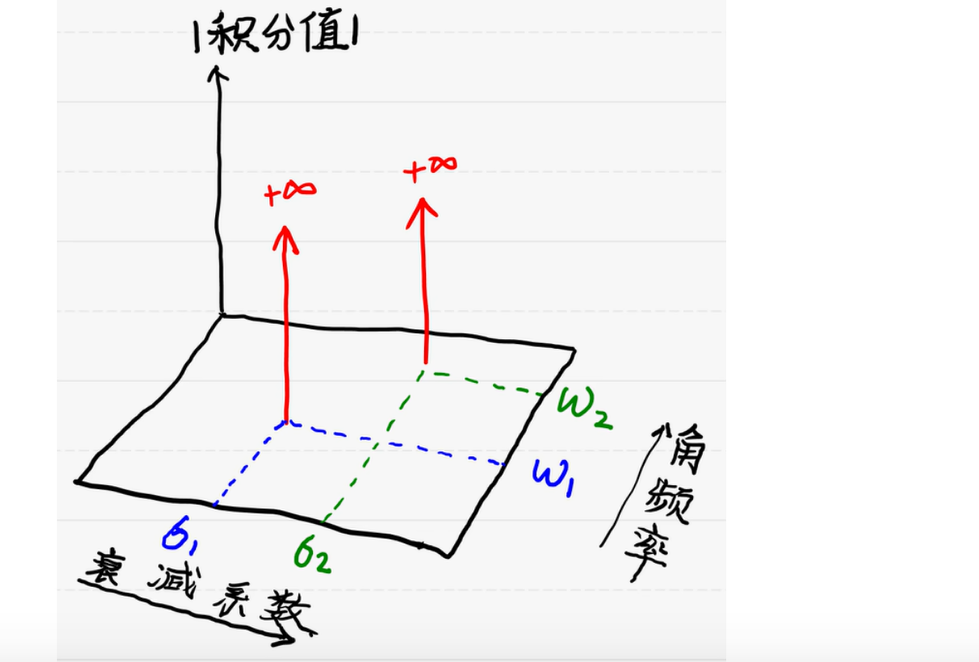
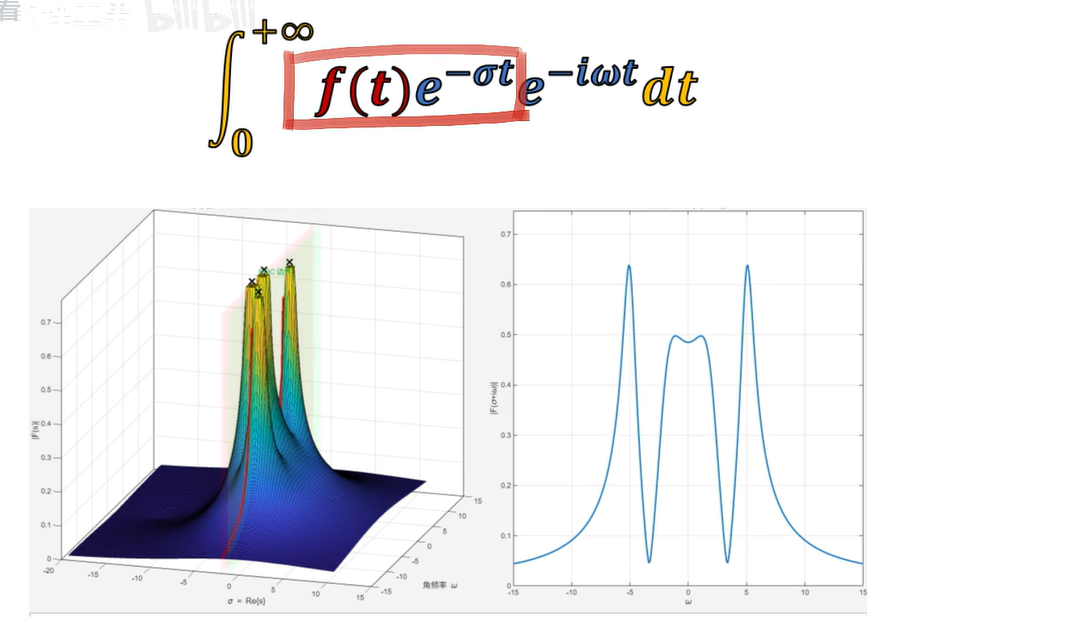
從公式本身，強化一下對作標記的理解，看到結果是一個關于σ、ω的二元函數。

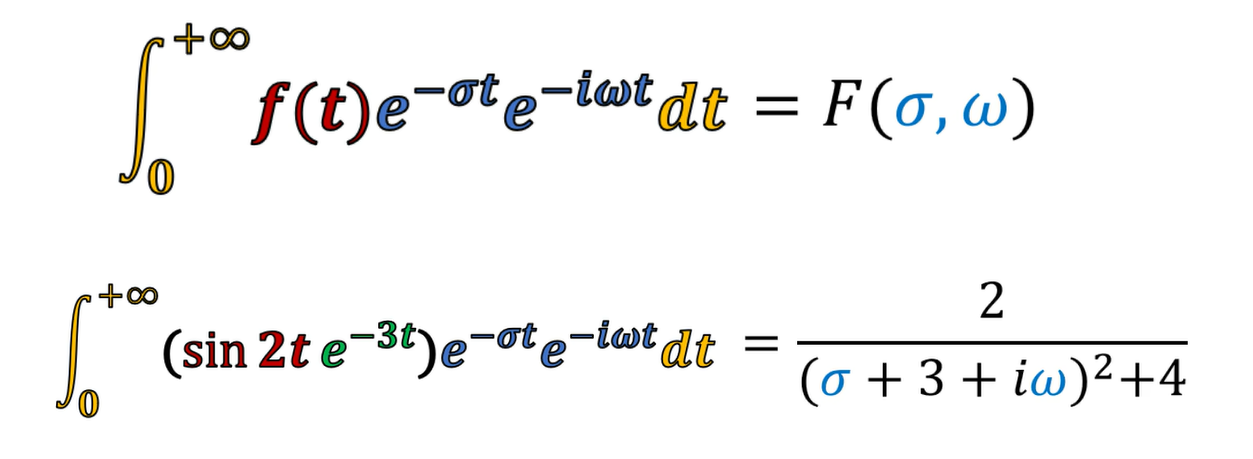
當σ = -3、ω = ±2的位置，結果的模長是無窮大的。

這兩個位置正好對應原函數中的振蕩頻率、衰減系數。

---

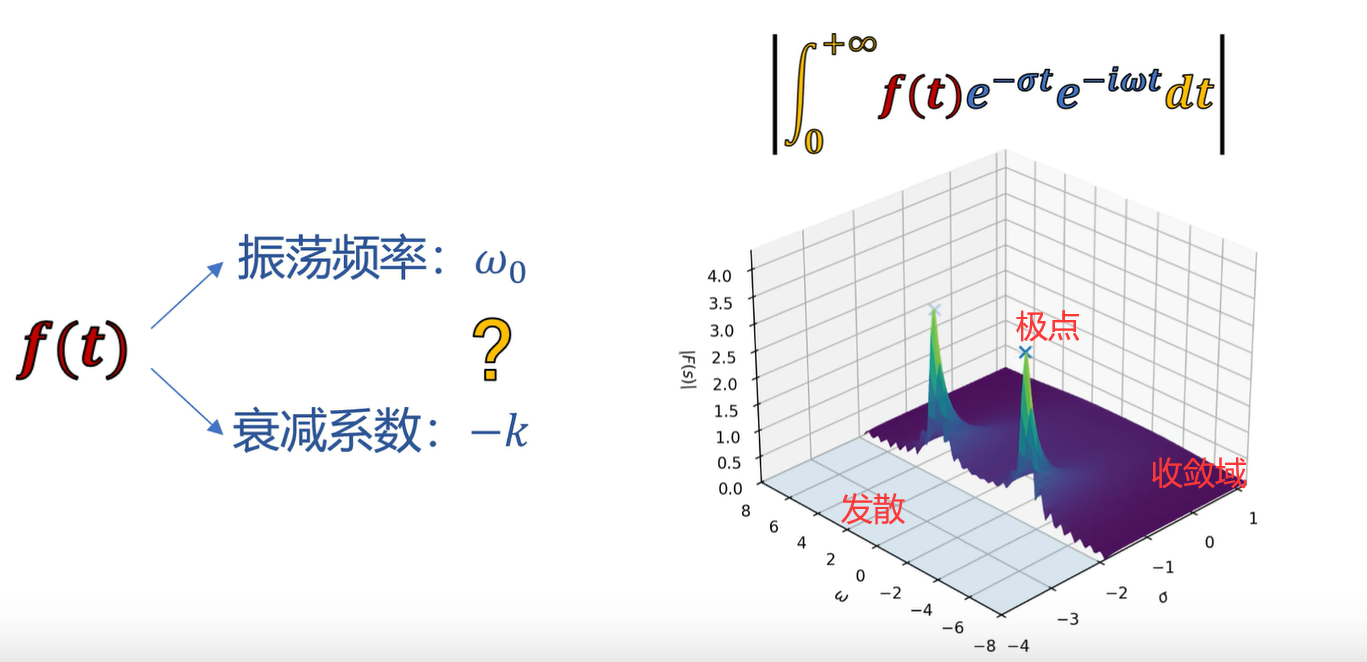
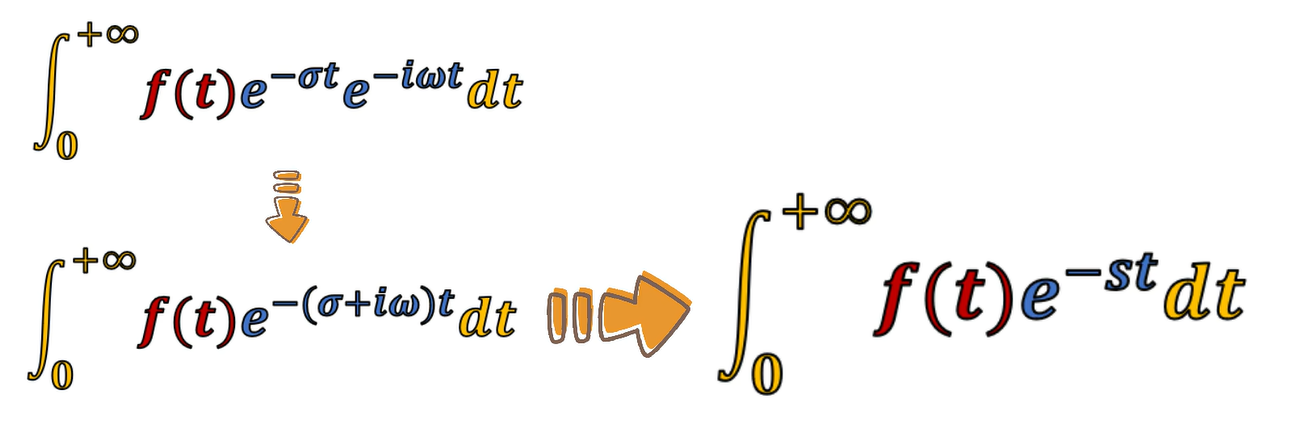
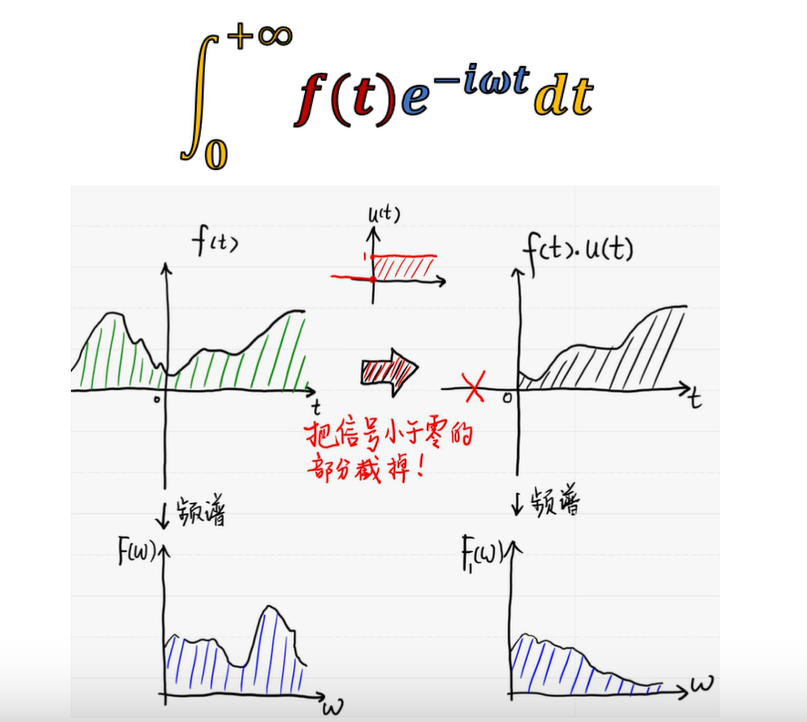
σ = 0時的（單邊）拉普拉斯變換就是單邊傅里葉變換。

σ ≠?0的拉普拉斯變換也可以看作傅里葉變換——加權傅里葉變換：

傅里葉變換重視基函數的歸一化，這樣子得到的頻率和能力的占比才準確。

拉普拉斯變換作為帶權傅里葉變換，原函數的能量會被這個權值給影響，它也就失去了能量占比的衡量的意義了，它的意義更多是在于幫助我們找到系統的瞬態——振蕩的頻率成分對應了多少的衰減。

這樣子就算原函數中的頻率成分不是衰減的，而是放大的，拉普拉斯變換也能處理，e^-σt不僅可以用來抵消衰減，也能夠用來抵消放大。