? ? ? ? 本期我們就來深入學習一下C++算法中一個很重要的算法思想:寬度優先搜索算法
? ? ? ? 寬度優先算法是一個應用十分廣泛的算法思想,涉及的領域也十分繁多,因此本篇我們先只涉獵它的一部分算法題:隊列/優先級隊列,后續我們會進一步地補充。
? ? ? ? 相關題解代碼已經上傳至作者的個人gitee:樓田莉子/C++算法學習喜歡請點個贊謝謝
目錄
基本概念
算法步驟
時間復雜度分析
應用場景
廣度優先搜索(BFS) vs. 深度優先搜索(DFS)算法對比
1、N叉樹的層序遍歷
2、二叉樹的鋸齒形層序遍歷
3、二叉樹最大寬度
4、在每個樹行中找最大值
5、最后一塊石頭的重量
6、數據流中的第K大元素
為什么選擇小根堆?
大根堆的缺點
7、前K個高頻單詞
基本概念
????????寬度優先搜索(Breadth-First Search,簡稱BFS)是一種用于遍歷或搜索樹或圖數據結構的算法。它從根節點開始,首先訪問所有相鄰節點,然后再逐層向下訪問更遠的節點。BFS屬于盲目搜索算法,不使用問題領域的任何啟發式信息。
算法步驟
-
初始化:
- 創建一個隊列Q用于存儲待訪問節點
- 將起始節點S標記為已訪問(通常使用顏色標記或布爾數組)
- 將S加入隊列Q
-
循環處理:
- 當Q不為空時: a. 從Q中取出隊首節點V b. 訪問節點V(根據具體應用可能是檢查、處理等操作) c. 將V的所有未被訪問的鄰接節點標記為已訪問并加入隊列Q
-
終止條件:
- 當隊列為空時,算法結束
時間復雜度分析
- 鄰接表表示:O(V + E),其中V是頂點數,E是邊數
- 鄰接矩陣表示:O(V2)
- 空間復雜度:O(V)(最壞情況下需要存儲所有節點)
應用場景
-
最短路徑問題:
- 在無權圖中尋找兩個節點間的最短路徑
- 示例:迷宮求解、社交網絡中尋找最少中間人
-
網絡爬蟲:
- 搜索引擎爬蟲按層級抓取網頁
- 先抓取種子頁面,然后抓取這些頁面鏈接的所有頁面
-
廣播網絡:
- 在計算機網絡中傳播信息包
- 在P2P網絡中定位資源
-
社交網絡分析:
- 尋找某人的N度人際關系
- 計算社交影響力
-
連通性檢測:
- 檢查圖中所有節點是否連通
- 尋找圖中的連通分量
廣度優先搜索(BFS) vs. 深度優先搜索(DFS)算法對比
| 特性維度 | 廣度優先搜索 (BFS) | 深度優先搜索 (DFS) |
|---|---|---|
| 核心數據結構 | 隊列 (Queue)?(FIFO) | 棧 (Stack)?(LIFO) (或系統的遞歸調用棧) |
| 遍歷思想/順序 | 逐層遍歷?(Level Order)。從起點開始,優先訪問所有相鄰節點,再訪問相鄰節點的相鄰節點。 | 一路到底?(Depth Order)。從起點開始,沿著一條路徑盡可能深地探索,直到盡頭再回溯。 |
| 空間復雜度 | O(b^d)?(對于樹結構,b為分支因子,d為目標所在深度) 在最壞情況下,需要存儲一整層的節點,對于空間消耗較大。 | O(h)?(對于樹結構,h為樹的最大深度) 通常只需存儲當前路徑上的節點,空間消耗相對較小。 |
| 完備性 | 是。如果解存在,BFS(在有限圖中)一定能找到解。 | 否(無限圖)。如果樹深度無限且解不在左側分支,DFS可能永遠無法找到解。在有限圖中是完備的。 |
| 最優性 | 是(未加權圖)。BFS按層擴展,首次找到的目標節點一定是經過邊數最少的(最短路徑)。 | 否。DFS找到的解不一定是路徑最短的,它取決于遍歷順序和運氣。 |
| 常見應用場景 | 1.?尋找最短路徑(未加權圖) 2. 系統性的狀態空間搜索(如謎題求解) 3. 查找網絡中所有節點(如社交網絡的“好友推薦”) | 1.?拓撲排序 2.?檢測圖中環 3.?路徑查找(所有可能解,如迷宮問題) 4. 圖的連通分量分析 |
| 實現方式 | 通常使用迭代和隊列實現。 | 使用遞歸實現最簡潔,也可使用迭代和顯式棧(Stack)?實現。 |
| 直觀比喻 | “水波紋”擴散:像一塊石頭投入水中,漣漪一圈一圈地向外擴展。 | “走迷宮”:選擇一條路一直走下去,直到死胡同,然后返回到最后一個岔路口選擇另一條路。 |
1、N叉樹的層序遍歷

? ? ? ? 算法思想:
????????
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {if(root==nullptr) return {};vector<vector<int>> ret;queue<Node*>q;q.push(root);while(!q.empty()){vector<int>level;int n=q.size();//求本層的個數for(int i=0;i<n;i++){Node* cur=q.front();q.pop();level.push_back(cur->val);for(auto& x:cur->children)//下一層結點入隊{q.push(x);}}ret.push_back(level);}return ret;}
};2、二叉樹的鋸齒形層序遍歷
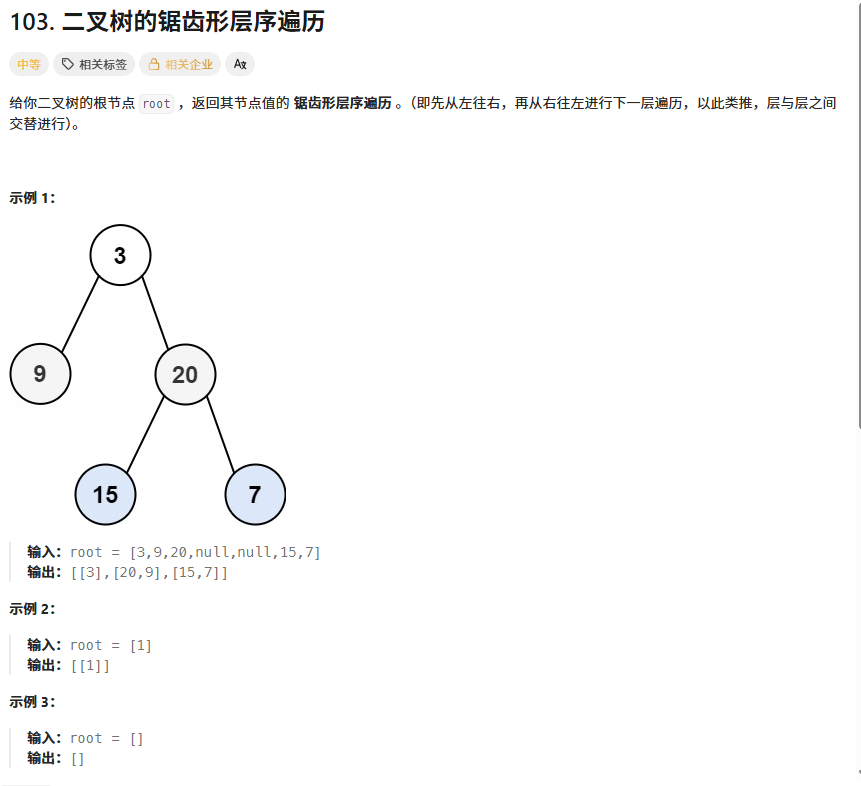
? ? ? ? 算法思想:
-
廣度優先搜索(BFS):使用隊列進行標準的層序遍歷,按層處理節點。
-
方向標志:使用一個布爾變量?
Is?來標記當前層是否需要反轉。初始為?false,表示第一層從左到右。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if(root==nullptr) return {}; // 如果根節點為空,返回空數組vector<vector<int>>ret; // 存儲最終結果queue<TreeNode*>q; // 輔助隊列用于BFSq.push(root); // 將根節點加入隊列bool Is=false; // 方向標志,false表示從左到右,true表示從右到左while(!q.empty()){ vector<int>level; // 存儲當前層的節點值int n=q.size(); // 當前層的節點數for(int i=0;i<n;i++){auto it=q.front(); // 取出隊首節點q.pop();level.push_back(it->val); // 將節點值加入當前層數組if(it->left) q.push(it->left); // 將左子節點加入隊列if(it->right) q.push(it->right); // 將右子節點加入隊列} if(Is) // 如果需要反轉當前層{reverse(level.begin(),level.end()); // 反轉當前層數組ret.push_back(level); // 將反轉后的數組加入結果Is=!Is; // 切換方向標志} else // 如果不需要反轉{ret.push_back(level); // 直接加入結果Is=!Is; // 切換方向標志}} return ret; // 返回最終結果}
};3、二叉樹最大寬度
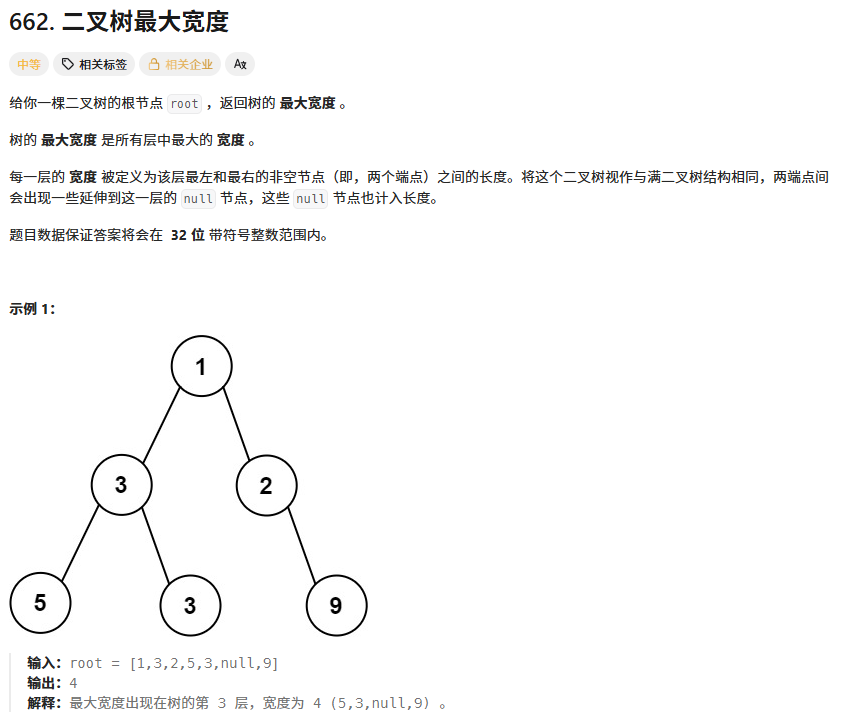
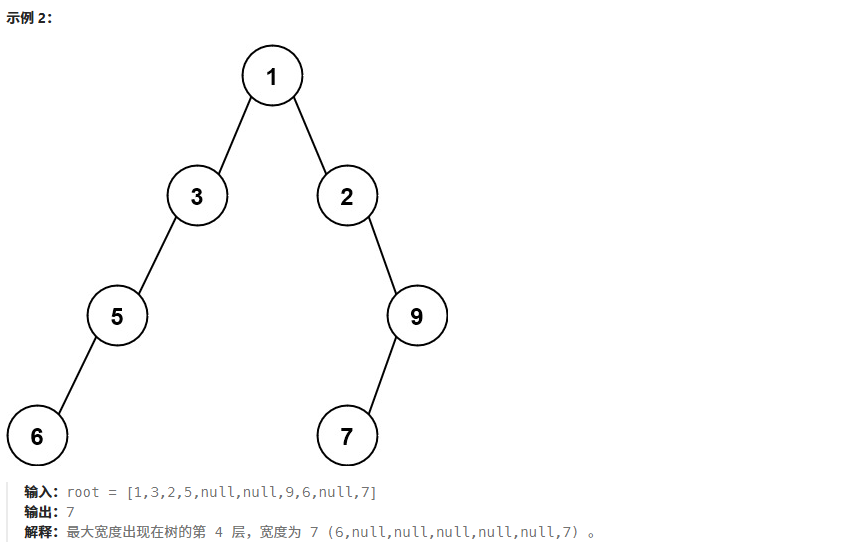
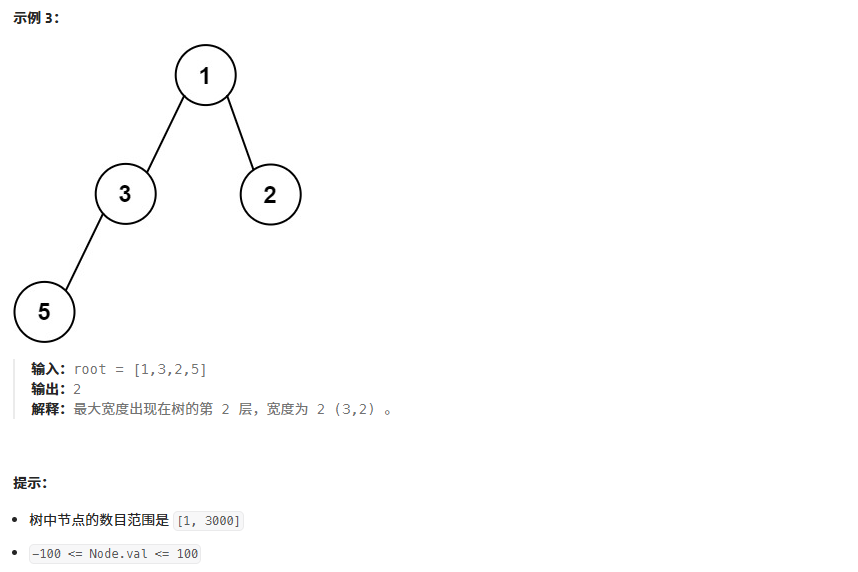
? ? ? ? 算法思想:利用數組存儲二叉樹的方式,給結點編號
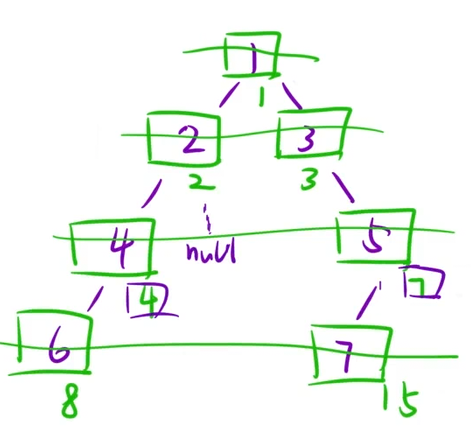
? ? ? ? 細節:下標有可能溢出
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {vector<pair<TreeNode*,unsigned int>>q;//數組模擬隊列q.push_back({root,1});unsigned int ret=0;//統計最終結果while(q.size()){//先更新auto&[x1,y1]=q[0];auto&[x2,y2]=q.back();ret=max(ret,y2-y1+1);//下一層進隊vector<pair<TreeNode*,unsigned int>>tmp;//下一層進第二個組for(auto&[x,y]:q){if(x->left) tmp.push_back({x->left,y*2});if(x->right) tmp.push_back({x->right,y*2+1});}q=tmp;}return ret;}
};4、在每個樹行中找最大值
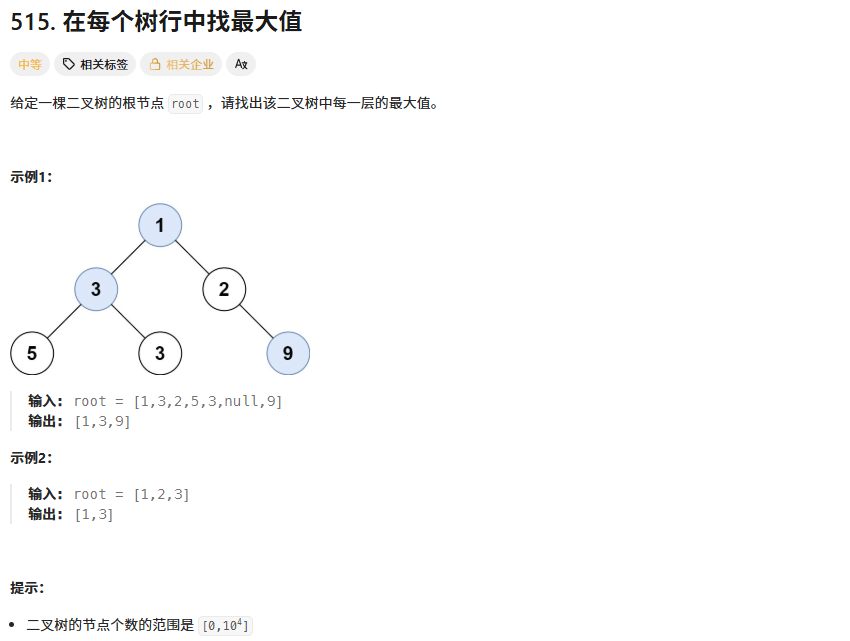
? ? ? ? 算法思想:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> largestValues(TreeNode* root) {if(root==nullptr) return {};vector<int>ret;queue<TreeNode*>q;q.push(root);while(!q.empty()){TreeNode*cur=root;int n=q.size();int a=INT_MIN;//初始化為無窮小for(int i=0;i<n;i++){auto it=q.front();q.pop();a=max(a,it->val);if(it->left) q.push(it->left);if(it->right) q.push(it->right);}ret.push_back(a);}return ret;}
};5、最后一塊石頭的重量

????????算法思想:
class Solution {
public:int lastStoneWeight(vector<int>& stones) {// 創建一個大根堆(優先級隊列默認是最大堆)// 這意味著隊列頂部始終是當前最大的元素priority_queue<int> q;// 將所有石頭重量加入優先級隊列for(auto& x : stones){q.push(x);}// 循環處理,直到隊列中只剩下一塊石頭或沒有石頭while(q.size() > 1){// 取出當前最重的石頭int a = q.top();q.pop();// 取出當前第二重的石頭int b = q.top();q.pop();// 如果兩塊石頭重量不相等,將差值重新加入隊列if(a > b) q.push(a - b);// 如果相等,兩者都粉碎,不需要操作(相當于都不加入隊列)}// 檢查隊列是否還有剩余石頭:如果有,返回頂部元素(最后一塊石頭的重量);否則返回0return q.size() ? q.top() : 0;}
};6、數據流中的第K大元素


? ? ? ? 算法思想:Top-K問題
? ? ? ? 堆(O(N*logk))或者快速選擇算法(O(N))
? ? ? ? 1、創建大根堆或者小根堆
? ? ? ? 2、元素一個一個進堆
? ? ? ? 3、判斷堆的大小是否超過K
class KthLargest {//創建一個大小為k的小根堆priority_queue<int,vector<int>,greater<int>>heap;int _k;public:KthLargest(int k, vector<int>& nums) {_k=k;for(auto&x:nums){heap.push(x);if(heap.size()>_k) heap.pop();}}int add(int val) {heap.push(val);if(heap.size()>_k) heap.pop();return heap.top();}
};/*** Your KthLargest object will be instantiated and called as such:* KthLargest* obj = new KthLargest(k, nums);* int param_1 = obj->add(val);*/為什么選擇小根堆?
-
問題需求:我們需要實時返回數據流中第K大的元素。這意味著我們需要維護前K大的元素,但只關心其中最小的那個(即第K大的元素)。
-
小根堆的優勢:
-
維護一個大小為K的小根堆,堆頂元素即為第K大的元素(因為堆頂是堆中最小的元素,而堆中所有元素都是當前最大的K個元素)。
-
添加新元素時,如果新元素大于堆頂元素,則替換堆頂并調整堆,時間復雜度為O(log K)。查詢操作直接返回堆頂,時間復雜度為O(1)。
-
整體效率高,適合數據流頻繁添加和查詢的場景。
-
大根堆的缺點
-
效率低下:如果使用大根堆存儲所有元素,每次查詢第K大的元素時,需要從堆中彈出K-1個元素才能訪問到第K大的元素。這會破壞堆的結構,且每次查詢的時間復雜度為O(K log n)(因為彈出操作需要調整堆)。
-
空間浪費:大根堆需要存儲所有元素,而不僅僅是前K大的元素,因此空間復雜度為O(n),而不是O(K)。
-
查詢成本高:每次查詢都需要執行彈出和重新插入操作(或者復制堆),導致整體性能較差,尤其當K較大或數據流很大時,無法滿足實時性要求。
大根堆的代碼(不推薦這個寫法)
#include <vector>
#include <queue>
using namespace std;class KthLargest {
private:priority_queue<int> maxHeap; // 大根堆,存儲所有元素int k;public:KthLargest(int k, vector<int>& nums) {this->k = k;for (int num : nums) {maxHeap.push(num);}}int add(int val) {maxHeap.push(val); // 添加新元素到大根堆// 創建臨時堆副本,避免破壞原堆priority_queue<int> temp = maxHeap;// 彈出K-1個最大元素,使堆頂變為第K大的元素for (int i = 0; i < k - 1; i++) {temp.pop();}return temp.top(); // 返回第K大的元素}
};7、前K個高頻單詞

class Solution
{
public://老方法:stable_sort函數(穩定排序)// 仿函數// struct compare// {// bool operator()(const pair<string ,int>&kv1,const pair<string ,int>&kv2)// {// return kv1.second>kv2.second;// }// };// vector<string> topKFrequent(vector<string>& words, int k) // {// map<string ,int>countMap;// for(auto& str:words)// {// //統計次數// countMap[str]++;// }// //數據量很大的時候要建小堆// //數據量不大用大堆// //但是這里要按頻率所以不建議用小堆// //用排序和大堆都差不多// //不可以用sort直接去排序// //sort要求是隨機迭代器,只用string、vector、deque支持// vector<pair<string,int>>v(countMap.begin(),countMap.end());// //sort(v.begin(),v.end(),compare());// //sort不是一個穩定的排序// stable_sort(v.begin(),v.end(),compare());//穩定的排序算法// vector<string>ret;// //取出k個// for(int i=0;i<k;i++)// {// ret.push_back(v[i].first);// }// return ret;//方法二:仿函數//仿函數// struct compare// {// bool operator()(const pair<string ,int>&kv1,const pair<string ,int>&kv2)// {// return kv1.second>kv2.second||(kv1.second==kv2.second&&kv1.first<kv2.first);// }// };// vector<string> topKFrequent(vector<string>& words, int k) // {// map<string ,int>countMap;// for(auto& str:words)// {// //統計次數// countMap[str]++;// }// //數據量很大的時候要建小堆// //數據量不大用大堆// //但是這里要按頻率所以不建議用小堆// //用排序和大堆都差不多// //不可以用sort直接去排序// //sort要求是隨機迭代器,只用string、vector、deque支持// vector<pair<string,int>>v(countMap.begin(),countMap.end());// //仿函數可以控制比較邏輯// sort(v.begin(),v.end(),compare());//穩定的排序算法// vector<string>ret;// //取出k個// for(int i=0;i<k;i++)// {// ret.push_back(v[i].first);// }// return ret;//方法三:優先級隊列struct compare{bool operator()(const pair<string, int>& kv1, const pair<string, int>& kv2) const{// 比較邏輯:頻率高優先,頻率相同則字典序小優先return kv1.second < kv2.second || (kv1.second == kv2.second && kv1.first > kv2.first);}};vector<string> topKFrequent(vector<string>& words, int k) {map<string, int> countMap;for(auto& str : words){countMap[str]++;}//數據量很大的時候要建小堆//數據量不大用大堆//但是這里要按頻率所以不建議用小堆//用排序和大堆都差不多//不可以用sort直接去排序//sort要求是隨機迭代器,只用string、vector、deque支持//建立大堆//priority_queue默認為大堆//不寫仿函數的時候priority_queue按pair比,pair默認按小于比// - 元素類型: pair<string, int>// - 容器類型: vector<pair<string, int>>// - 比較器類型: compare (去掉括號)priority_queue<pair<string, int>,vector<pair<string, int>>,compare> pq(countMap.begin(), countMap.end());vector<string> ret;for(int i = 0; i < k; i++){ret.push_back(pq.top().first);pq.pop();}return ret;}
};
? ? ? ? 本期內容就到這里,喜歡請點個贊謝謝








實戰十八——圖像透視轉換)


:(十三)堆的應用)







