數據結構（C語言篇）：（十三）堆的應用

前言

????????堆作為一種高效且靈活的樹形結構，在算法設計與優化中扮演著重要角色。其獨特的性質——完全二叉樹形態與父子節點間的有序性，使得堆能夠以對數級時間復雜度動態維護極值，從而為兩類經典問題提供優雅解決方案：堆排序利用大頂堆或小頂堆實現無需遞歸的原地排序，將時間復雜度穩定控制在O(nlogn)；而TOP-K問題則通過堆的極值篩選特性，在海量數據場景下以O(nlogk)的代價快速定位關鍵元素。無論是排序場景的性能平衡，還是大數據處理的效率優化，堆結構的應用都展現出算法設計與工程實踐的深度結合。本文將系統解析這兩類問題的技術實現與核心思想。下面就讓我們正式開始吧！

一、堆排序

1.1? 版本一：基于已有數組建堆、取堆頂元素完成排序

1.1.1? 實現邏輯

創建并初始化堆：定義HP類型的堆變量hp，通過HPInit初始化。
構建堆：遍歷數組arr，通過HPPush將每個元素插入堆中（插入過程會自動維護堆的性質）。
提取堆頂元素：循環從堆中獲取堆頂元素（HPTop），依次存入原數組arr，然后通過HPPop刪除堆頂元素。
銷毀堆：排序完成后調用HPDesTroy釋放堆占用的資源。

? ? ? ? 完整代碼如下所示：

//堆排序----這不是實際的堆排序
void HeapSort01(int* arr,int n)
{HP hp;//-----使用數據結構-堆HPInit(&hp);//調用push將數組中的數據放入到堆中for (int i = 0; i < n; i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDesTroy(&hp);
}

1.1.2? 底層原理

? ? ? ? 排序過程的本質是這樣的：

若使用小堆：每次提取的堆頂是當前剩余元素的最小值，依次存入數組會得到升序結果
若使用大堆：每次提取的堆頂是當前剩余元素的最大值，依次存入數組（需從后往前存）會得到升序結果

? ? ? ? 這種堆排序方法的整體時間復雜度為，時間復雜度的計算主要需要考慮下面兩種操作：

構建堆：n次HPPush，每次，總復雜度
提取元素：n次HPTop（）和HPPop（），總復雜度。

1.1.3? 應用示例

????????假設堆為小堆（AdjustUp和AdjustDown均按小堆邏輯實現），則應用示例如下所示：

// 假設已實現HPTop函數（獲取堆頂元素）
HPDataType HPTop(HP* php) {assert(php && !HPEmpty(php));return php->arr[0];
}// 排序示例
int main() {int arr[] = {3, 1, 4, 1, 5, 9, 2, 6};int n = sizeof(arr) / sizeof(arr[0]);HeapSort01(arr, n);// 輸出排序結果（升序）for (int i = 0; i < n; i++) {printf("%d ", arr[i]); // 輸出：1 1 2 3 4 5 6 9}return 0;
}

1.1.4? 執行流程

????????以數組[3, 1, 2]為例，執行流程如下所示：

? ? ? ? （1）初始化堆：HPInit(&hp)創建空堆。

? ? ? ? （2）元素入堆：

插入 3：堆為[3]；
插入 1：經AdjustUp調整后堆為[1, 3]；
插入 2：經AdjustUp調整后堆為[1, 3, 2]（小堆性質：1≤3 且 1≤2）。

? ? ? ? （3）元素出堆存回數組：

第一次：HPTop獲取 1，存入arr[0]，HPPop后堆變為[2, 3]；
第二次：HPTop獲取 2，存入arr[1]，HPPop后堆變為[3]；
第三次：HPTop獲取 3，存入arr[2]，HPPop后堆為空。

? ? ? ? （4）銷毀堆：HPDesTroy(&hp)釋放資源，排序完成，數組變為[1, 2, 3]

? ? ? ? 為什么說這種堆排序“不是實際的堆排序”呢？

? ? ? ? 這種方法實現的堆排序與標準堆排序的核心區別在于空間效率：

? ? ? ? 標準堆排序是直接在原數組上構建堆（原地建堆）的，通過 "堆頂與末尾元素交換 + 向下調整" 實現排序，不需要額外的堆結構，空間復雜度為；

? ? ? ? 而這種堆排序需要額外創建一個堆結構存儲所有元素，空間復雜度為，本質是 "借助堆的特性實現排序"，而非嚴格意義上的原地堆排序。

? ? ? ? 除此之外，標準堆排序的建堆過程是通過AdjustDown從后往前調整（時間復雜度為），而該函數通過HPPush建堆（時間復雜度為），建堆效率是比較低的。

1.2? 版本二：原地排序 —— 標準堆排序

? ? ? ? 標準堆排序的核心思路在于：數組建堆，首尾交換，交換后的堆尾數據從堆中刪掉，將堆頂數據向下調整選出次大的數據。

1.2.1? 實現邏輯

? ? ? ? 標準堆排序的核心操作主要分為兩個階段：

（1）建堆階段：

? ? ? ? 首先從最后一個非葉子節點（從索引（n-1-1）/ 2）開始，向前遍歷至根節點；

? ? ? ? 然后對于每個結點執行AdjustDown（向下調整），將無序數組轉換為堆（默認實現為大堆，便于升序排序）。

（2）排序階段：

定義end指向當前堆的最后一個元素（初始為n-1）；
循環交換堆頂（索引0，當前最大值）與end位置的元素，將最大值 "沉" 到數組末尾；
對新堆頂（原end位置元素）執行AdjustDown，調整范圍為[0, end)（排除已排好的末尾元素）；
減小end，重復操作直到end為0（所有元素排序完成）。

? ? ? ? 完整代碼的實現如下：

//堆排序————使用的是堆結構的思想 n * logn
void HeapSort(int* arr, int n)
{//向下調整算法——建堆nfor (int i = (n - 1 - 1)/2; i >= 0; i--){AdjustDown(arr, i, n);}////向上調整算法建堆n*logn//for (int i = 0; i < n; i++)//{//	AdjustUp(arr, i);//}//n*lognint end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);//lognend--;}
}

1.2.2? 底層原理

建堆的選擇：

? ? ? ? 標準堆排序優先使用AdjustDown從后往前建堆，時間復雜度為；

? ? ? ? 上述代碼中的AdjustUp從前往后建堆，時間復雜度為，因此前者更高效；

????????建堆選擇大堆的原因：大堆的堆頂是最大值，每次交換后可將最大值放到數組末尾，直接形成升序。

原地排序的實現：

????????無需額外空間，直接在原數組上通過索引操作實現堆結構（利用完全二叉樹的父子節點索引關系）；

????end變量的作用是劃分 "未排序的堆區域" 和 "已排序的末尾區域"，隨著循環逐漸縮小堆區域。

1.2.3? 時間復雜度計算

????????

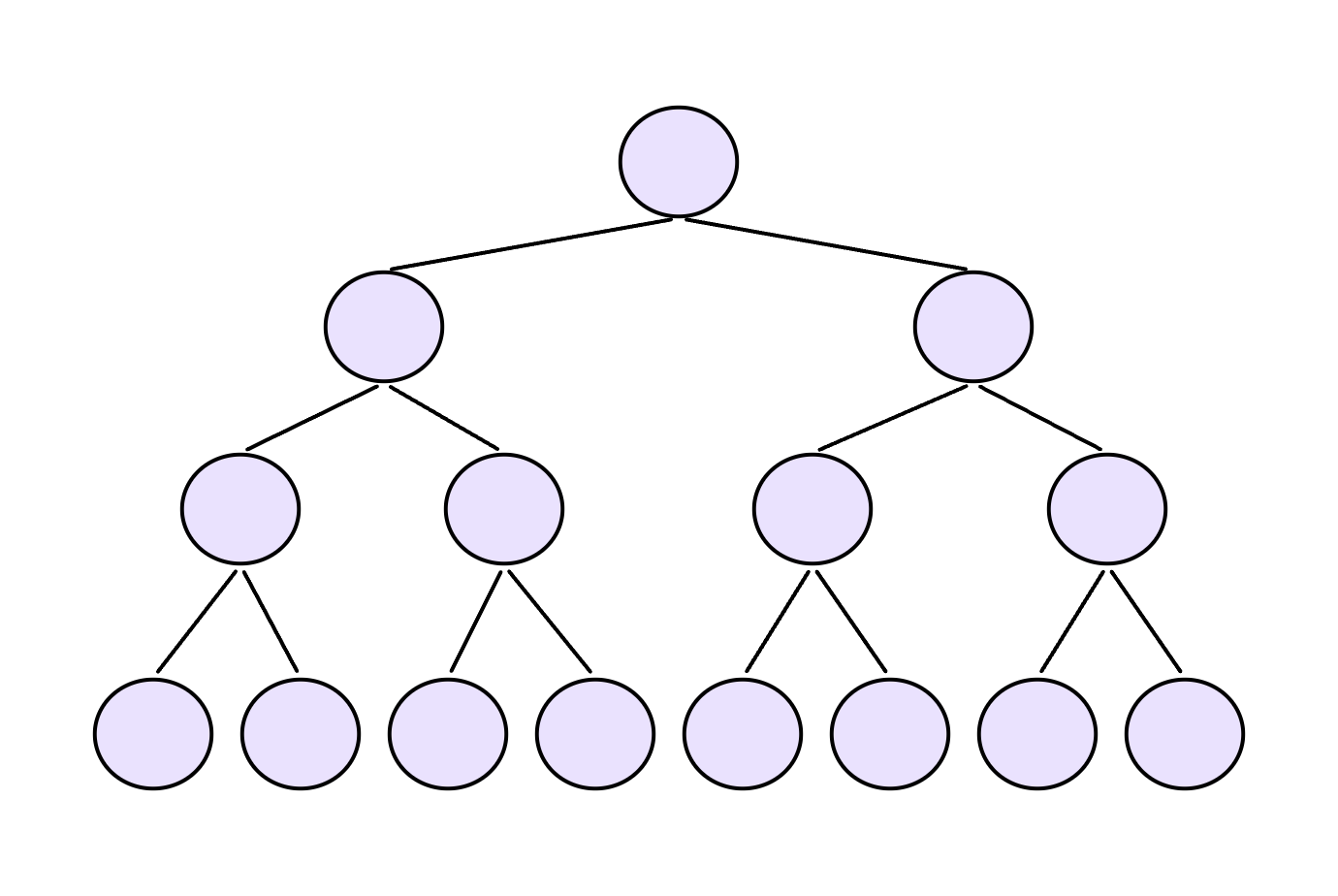
? ? ? ? 分析如下：

? ? ? ? 第1層，有個結點，交換到根結點后，需要向下移動0層；

????????第2層，有個結點，交換到根結點后，需要向下移動1層；

????????第3層，有個結點，交換到根結點后，需要向下移動2層；

? ? ? ? ……

????????第h層，有個結點，交換到根結點后，需要向下移動h-1層。

? ? ? ? 由此我們可以發現，堆排序第二個循環中的向下調整與建堆中的向上調整算法的時間復雜度計算是一致的，故在這博主就不再過多贅述了。大家如果感興趣的話可以去看看我上一期的博客。

? ? ? ? 最終可以計算得到堆排序的時間復雜度為
?

二、TOP-K問題

? ? ? ? TOP-K問題就是求數據結合中前K個最大的元素或者最小的元素，一般情況下數據量都是比較大的。

? ? ? ? 比如：專業前10名、世界500強、富豪榜、游戲中前100的活躍玩家等。

? ? ? ? 對于TOP-K問題，我們能夠想到的最簡單直接的方法就是進行排序。但是，如果數據量非常大時，排序的效率就會變得很低（可能出現數據不能一下全部加載到內存中的情況）。因此解決TOP-K問題的最佳方式是使用堆，基本思路如下：

（1）用數據集合中的前K個元素來建堆：

? ? ? ? 如果用前K個最大的元素，則建小堆；如果用前K個最小的元素，則建大堆。

（2）用剩余的N-K個元素依次與堆頂元素來比較，不滿足則替換堆頂元素：

? ? ? ? 將剩余N-K個元素依次與堆頂元素比完之后，堆中剩余的K個元素就是所求的前K個最小或者最大的元素。

? ? ? ? 要解決TOP-K問題，我們需要先利用C語言篇學到的文件操作的相關知識，來造一些數據：

void CreateNDate()
{// 造數據int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}

? ? ? ? 這樣我們就生成了100000個隨機數，并把它們存儲在了“data.txt”文件中。

? ? ? ? 下面我們就來正式嘗試解決一下TOP-K問題：

2.1? 實現邏輯

（1）獲取用戶輸入K：通過scanf讀取需要查找的前 K 個元素數量。

（2）文件操作初始化：打開數據文件data.txt，處理文件打開失敗的異常。

（3）創建小堆：

動態分配大小為 K 的數組minHeap（用于存儲候選的前 K 個最大元素）；
從文件中讀取前 K 個數據存入數組；
通過AdjustDown將數組調整為小堆（堆頂為當前 K 個元素中的最小值）。

（4）篩選剩余數據：

遍歷文件中剩余的所有數據；
若當前數據大于小堆的堆頂（說明該數據比當前候選的最小元素更大，有資格進入前 K），則替換堆頂并通過AdjustDown重新調整為小堆。

（5）輸出結果：循環結束后，小堆中存儲的就是整個文件中最大的前 K 個元素，打印輸出。

（6）資源釋放：關閉文件。

? ? ? ? 完整代碼如下所示：

void TopK()
{int k = 0;printf("請輸入K：");scanf("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail!");exit(1);}//申請空間大小為k的整型數組int* minHeap = (int*)malloc(sizeof(int) * k);if (minHeap == NULL){perror("malloc fail!");exit(2);}//讀取文件中k個數據放到數組中for (int i = 0; i < k; i++){fscanf(fout, "%d", &minHeap[i]);}//數組調整建堆--向下調整建堆//找最大的前K個數，建小堆for (int i = (k-1-1)/2; i >= 0; i--){AdjustDown(minHeap, i, k);}//遍歷剩下的n-k個數，跟堆頂比較，誰大誰入堆int data = 0;while (fscanf(fout,"%d",&data) != EOF){if (data > minHeap[0]){minHeap[0] = data;AdjustDown(minHeap, 0, k);}}//打印堆里的數據for (int i = 0; i < k; i++){printf("%d ", minHeap[i]);}printf("\n");fclose(fout);
}

2.2? 底層原理

2.2.1? 為何使用小堆而非大堆？

? ? ? ? 我們的目標是找 “最大的前 K 個元素”，小堆的堆頂是當前候選集中的最小值。當新元素大于堆頂時，說明它比候選集中最小的元素更大，是有資格替換堆頂進入候選集的。

????????若使用大堆，堆頂是候選集中的最大值，是無法通過簡單比較判斷新元素是否應進入候選集的（新元素可能比堆頂小但比其他元素大）。

2.2.2? 時間復雜度優化

????????在傳統方法中，是對所有數據排序后取前 K 個，時間復雜度為（n 為數據總量）。

? ? ? ? 在堆解法中，建堆時間為，遍歷剩余數據并調整堆的時間為，整體復雜度為。當 n 極大（如百萬 / 億級）且 K 較小時（如 100），性能優勢是十分顯著的。

2.2.3? 空間復雜度優勢

? ? ? ? 堆解法僅需要的空間存儲小堆，適合處理無法一次性加載到內存的海量數據（如大文件）。

2.3? 應用示例

????????假設data.txt中存儲以下數據（共 10 個元素）：

5 9 3 12 7 15 2 8 11 6

????????當用戶輸入k=3時，期望輸出最大的 3 個元素：15、12、11。

????????首先讀取前 3 個數據[5, 9, 3]，建小堆后為[3, 9, 5]（堆頂 3 是當前最小值）

? ? ? ? 接著遍歷剩余數據：

????????????????12 > 3 → 替換堆頂為 12，調整后小堆為[5, 9, 12]；

????????????????7 > 5 → 替換堆頂為 7，調整后小堆為[7, 9, 12]；

????????????????15 > 7 → 替換堆頂為 15，調整后小堆為[9, 15, 12]；

????????????????2 ≤ 9 → 不處理；

????????????????8 ≤ 9 → 不處理；

????????????????11 > 9 → 替換堆頂為 11，調整后小堆為[11, 15, 12]；

????????????????6 ≤ 11 → 不處理。

????????最終小堆[11, 15, 12]中存儲的就是最大的 3 個元素（輸出順序可能因堆結構而略有不同）。