做機器人逆運動學(IK)的時候,你遲早會遇到矩陣指數和對數這些東西。為什么呢?因為計算三維旋轉的誤差,不能簡單地用歐氏距離那一套,那只對位置有效。旋轉得用另一套方法——你需要算兩個旋轉矩陣之間的差異,這就涉及到矩陣對數了。
這篇文章就是要把這事兒說清楚:從旋轉矩陣構成的李群開始,到流形和切空間,再到怎么用叉積算旋轉矩陣的導數,如何對旋轉矩陣做增量更新,最后是如何計算從一個姿態到另一個姿態需要的角速度。
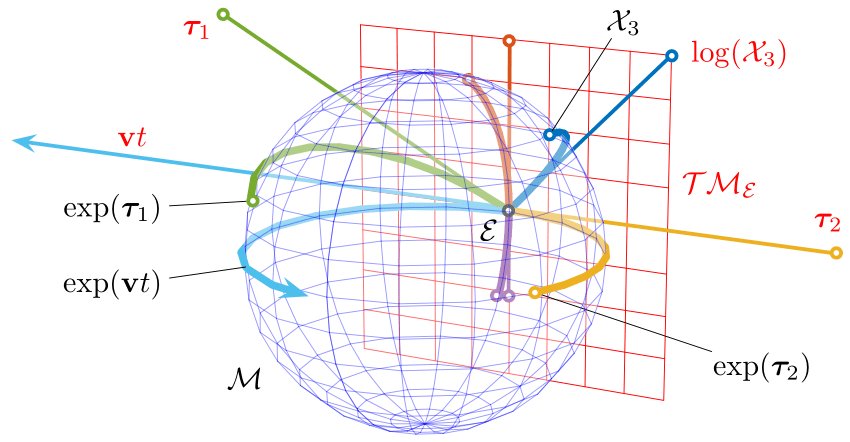
SO(3):三維旋轉的數學結構
機器人的姿態其實就是一個三維坐標系。這個坐標系由三個互相垂直、長度為1的向量組成,比如最簡單的情況:(1,0,0)?、(0,1,0)?、(0,0,1)?。把這三個向量當作列向量排在一起,就得到了一個3×3的旋轉矩陣。
雖然這個矩陣在數學上屬于?3?3空間,但實際上能表示旋轉的矩陣組合要少得多,它們形成一個特殊的群,叫做三維特殊正交群SO(3)。類似的還有二維旋轉SO(2)、四維變換矩陣等等,這些都屬于李群家族。
流形和切空間:幾何概念
實數是一條直線,但SO(3)不是,它在?3?3里形成一個彎曲的流形。這個流形是連續的、可微的,你可以在上面定義距離。想在這個彎曲的表面上移動,就得沿著切線方向走,這就引出了切空間的概念。

就像函數的切線斜率由導數決定一樣,我們也可以通過計算流形切線的"斜率"來得到它的導數。
計算旋轉矩陣的導數
現在問題來了:一個旋轉矩陣R和一個角速度向量ω,怎么算R的變化率??
答案是這樣的:
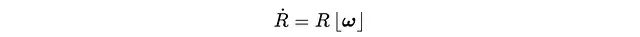
這里?ω?是ω對應的反對稱矩陣:
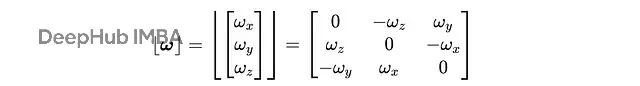
為什么要搞成反對稱矩陣?因為實際上是想算ω和R每一列的叉積。有時候你會看到這個操作寫成帽子符號,都是一個意思。
所有3×3實反對稱矩陣構成的空間叫做𝖘𝖔(3),這是SO(3)的李代數,也就是SO(3)在單位矩陣處的切空間。雖然它在矩陣乘法下不構成群,但它是個李代數,讓我們能在非線性的SO(3)流形上做線性計算。
叉積的幾何意義
我們來仔細看看叉積ω×v是什么意思。兩個向量的叉積結果是一個同時垂直于這兩個向量的新向量,長度正比于兩向量夾角的正弦值。
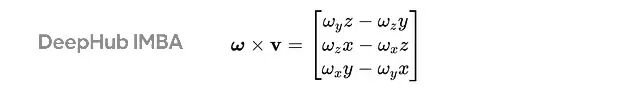
把ω變成反對稱矩陣形式,就能用矩陣乘法實現叉積運算:
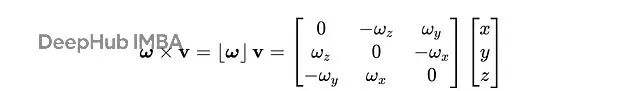
對矩陣R做這個操作,就等于對R的每一列都做一次叉積。
這里有個細節要注意:這個運算可以左乘也可以右乘,取決于ω是在機體坐標系還是世界坐標系下給出的。一般我們假設ω在機體坐標系,所以?ω?右乘到R上。
把ω想象成旋轉軸,|ω|是轉速,這樣理解叉積就直觀多了。如果v指向某個點,那么ω×v就是這個點繞ω軸旋轉時的速度方向。
矩陣指數:精確的旋轉更新
有了上面的理解,我們再看這個微分方程:
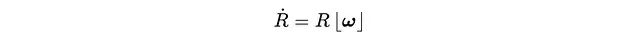
R的每一列代表一個坐標軸,和ω做叉積得到的矩陣描述了各個軸因為旋轉產生的速度。那怎么得到更新后的旋轉矩陣呢?
一個樸素的想法是用歐拉積分,就是把R?ω?乘個小時間步長然后加起來。但這樣做有問題:無法保證結果還是正交矩陣,也就是說可能跳出SO(3)。雖然可以每步都強制歸一化,但有更精確的方法。
上面那個微分方程其實是個線性常微分方程,解是:
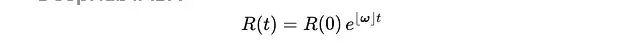
矩陣指數函數通過泰勒展開定義,大部分線性代數庫都有實現。
看看用這個方法繞ω=(1.0,1.0,1.0)?旋轉的效果:

矩陣對數:解決逆運動學問題
有時候我們需要反過來算:給定當前姿態R(0)和目標姿態R(t),需要什么旋轉向量才能從一個到另一個?這就像算位置的歐氏距離一樣。
對于旋轉,我們把R(0)移到等式另一邊,算矩陣對數,再除以時間t:
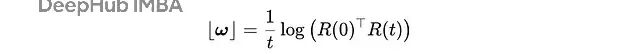
但事情還沒完。真正的逆運動學問題需要算誤差對關節角的導數。對于n個關節的機器人,我們要算一個3×n的雅可比矩陣:
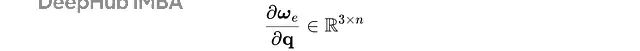
要對R(t)關于q求導,得先過一遍對數,然后用鏈式法則。具體怎么做,作者說在另一篇文章里有。
代碼實現
下面是生成上面動畫的代碼。關鍵是用scipy的expm函數實現矩陣指數,核心更新就是一行:
R = R @ expm(hat(omega) * dt)
。
import numpy as np
from scipy.linalg import expm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation def hat(omega): return np.array([ [0, -omega[2], omega[1]], [omega[2], 0, -omega[0]], [-omega[1], omega[0], 0] ]) # Angular velocity vector (rad/s)
omega = np.array([1.0, 1.0, 1.0]) dt = 0.05
T = 5
N = int(T / dt) # Initialize rotation matrix as identity
R = np.eye(3) # Store rotation matrices
Rs = [R.copy()]
for _ in range(N): R = R @ expm(hat(omega) * dt) Rs.append(R.copy()) fig = plt.figure()
ax = fig.add_subplot(111, projection='3d') # Set plot limits and labels
ax.set_xlim([-1.5, 1.5])
ax.set_ylim([-1.5, 1.5])
ax.set_zlim([-1.5, 1.5])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Rotating 3D Coordinate Frame') # Initialize quiver objects for x, y, z axes
quiver_x = ax.quiver(0, 0, 0, 1, 0, 0, color='r', length=1, normalize=True)
quiver_y = ax.quiver(0, 0, 0, 0, 1, 0, color='g', length=1, normalize=True)
quiver_z = ax.quiver(0, 0, 0, 0, 0, 1, color='b', length=1, normalize=True) def update(num): # Remove previous quivers (if any) for artist in ax.collections: artist.remove() R = Rs[num] x_axis = R[:, 0] y_axis = R[:, 1] z_axis = R[:, 2] ax.quiver(0, 0, 0, *x_axis, color='r', length=1, normalize=True) ax.quiver(0, 0, 0, *y_axis, color='g', length=1, normalize=True) ax.quiver(0, 0, 0, *z_axis, color='b', length=1, normalize=True) return [] ani = FuncAnimation(fig, update, frames=len(Rs), interval=50, blit=False) from matplotlib.animation import PillowWriter
ani.save("rotation.gif", writer=PillowWriter(fps=20)) plt.show()
總結
本文從理論到實踐全面介紹了矩陣指數在機器人逆運動學中的應用。我們從SO(3)李群和𝖘𝖔(3)李代數的數學結構出發,解釋了為什么旋轉計算需要特殊的數學工具。通過流形和切空間的幾何概念,我們理解了旋轉矩陣導數的計算方法,并學會了使用反對稱矩陣實現叉積運算。矩陣指數函數提供了精確的旋轉更新方法,能夠保證旋轉矩陣在更新過程中始終保持正交性,避免了傳統歐拉積分可能導致的數值不穩定問題。而矩陣對數則解決了逆向問題——如何計算從當前姿態到目標姿態所需的旋轉誤差和角速度。這套方法的核心優勢在于能夠在非線性的旋轉空間中進行精確計算,為逆運動學算法提供了必要的數學工具,特別是在計算雅可比矩陣時所需的旋轉導數。對于需要高精度姿態控制的機器人應用,這些數學工具是必不可少的。
https://avoid.overfit.cn/post/352201d5dfd749e48e2b6ccf8e81abf0
作者:Nikolaus Correll
實戰十八——圖像透視轉換)


:(十三)堆的應用)













)
)
