當磁化自旋系統被射頻脈沖擾動而偏離其熱平衡態后,一旦移除外部激勵并給予足夠時間,系統將根據熱力學定律返回平衡態。這一過程包含三個特征現象:
(a) 自由進動——宏觀磁化矢量 (M?\vec{M}M) 繞( B0?\vec {B_0}B0?? )場的進動;
(b) 縱向弛豫——縱向磁化分量(Mz{M_z}Mz?) 的恢復;
? 橫向弛豫——橫向磁化分量 (Mxy{M_{xy}}Mxy?) 的衰減。
弛豫過程源于原子核周圍由隨機熱運動產生的時變微觀磁場,但具體機制因自旋系統而異,過于復雜。實際上不管是激發還是弛豫,只有量子力學才能完全精確的給出數學解釋,此處僅通過布洛赫方程進行唯象描述,它提供足夠的精度,對MR成像而言也足夠了
忽略射頻激勵項后,在拉莫爾旋轉坐標系中,弛豫過程由以下方程描述:
{dMz′dt=?Mz′?Mz0T1dMx′y′dt=?Mx′y′T2(3.121)
\left\{
\begin{array}{l}
\frac{d M_{z'}}{d t} = -\frac{M_{z'} - M_z^0}{T_1} \\
\frac{d M_{x'y'}}{d t} = -\frac{M_{x'y'}}{T_2}
\end{array}
\right. \tag {3.121}
{dtdMz′??=?T1?Mz′??Mz0??dtdMx′y′??=?T2?Mx′y′???(3.121)
其中 Mz0M_z^0Mz0? 為熱平衡態縱向磁化強度,T1T_1T1? 和 T2T_2T2? 分別為描述縱向和橫向弛豫過程的時間常數。解方程 (3.121) 得:
{Mx′y′(t)=Mx′y′(0+)e?t/T2Mz′(t)=Mz0(1?e?t/T1)+Mz′(0+)e?t/T1(3.122)
\left\{
\begin{array}{l}
M_{x'y'}(t) = M_{x'y'}(0_+) e^{-t/T_2} \\
M_{z'}(t) = M_z^0 (1 - e^{-t/T_1}) + M_{z'}(0_+) e^{-t/T_1}
\end{array}
\right. \tag {3.122}
{Mx′y′?(t)=Mx′y′?(0+?)e?t/T2?Mz′?(t)=Mz0?(1?e?t/T1?)+Mz′?(0+?)e?t/T1??(3.122)
此處 Mx′y′(0+)M_{x'y'}(0_+)Mx′y′?(0+?) 和 Mz′(0+)M_{z'}(0_+)Mz′?(0+?) 分別表示射頻脈沖結束后,旋轉坐標系下觀測到的初始橫向和縱向磁化分量。
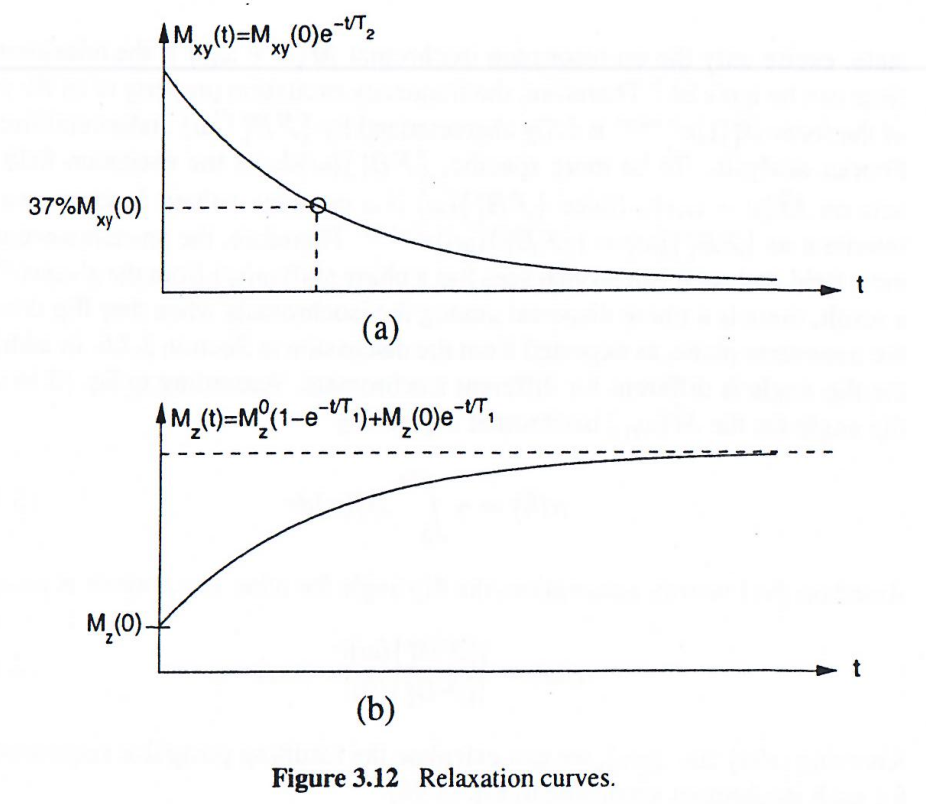
值得注意的是,T1T_1T1? 和 T2T_2T2? 并不是縱向和橫向弛豫的完成時間。為了說得更加清楚,假設熱平衡態下產生一個 x′x'x′ 軸90度射頻脈沖,在射頻脈沖激發前(t=0?)(t=0_{-})(t=0??)和射頻脈沖激發后(t=0+)(t=0_{+})(t=0+?)的橫向和縱向磁化分量如下所示:
{Mxy′(0?)=0Mz′(0?)=Mz0→90x′{Mxy′(0+)=Mz0Mz′(0+)=0
\begin{cases}
M_{xy^{\prime}}(0_{-}) = 0 \\
M_{z^{\prime}}(0_{-}) = M_{z}^{0}
\end{cases}
\xrightarrow{90_{x^{\prime}}}
\begin{cases}
M_{xy^{\prime}}(0_{+}) = M_{z}^{0} \\
M_{z^{\prime}}(0_{+}) = 0
\end{cases}
{Mxy′?(0??)=0Mz′?(0??)=Mz0??90x′??{Mxy′?(0+?)=Mz0?Mz′?(0+?)=0?
而在 t>0t>0t>0 的時的橫向和縱向磁化分量如下所示:
{Mx′y′(t)=Mz0e?t/T2Mz′(t)=Mz0(1?e?t/T1)
\left\{
\begin{array}{l}
M_{x'y'}(t) = M_{z}^{0} e^{-t/T_2} \\
M_{z'}(t) = M_z^0 (1 - e^{-t/T_1})
\end{array}
\right.
{Mx′y′?(t)=Mz0?e?t/T2?Mz′?(t)=Mz0?(1?e?t/T1?)?
然后定義,當橫向磁化分量衰減為初始值Mx′y′(0+)M_{x'y'}(0_+)Mx′y′?(0+?)的37%的時刻就是 T2T_2T2? ,而當縱向磁化分量恢復為熱平衡態時的63%的時刻就是 T1T_1T1?: {Mx′y′(T2)≈37%Mx′y′(0+)Mz′(T1)≈63%Mz0\left\{\begin{array}{l}M_{x'y'}(T_2) \approx 37\% M_{x'y'}(0_+)\\M_{z'}(T_1) \approx 63\% M_z^0 \end{array}\right.{Mx′y′?(T2?)≈37%Mx′y′?(0+?)Mz′?(T1?)≈63%Mz0??
生物組織典型值:
- T1T_1T1?范圍:300–2000 ms
- T2T_2T2?范圍:30–150 ms
- 對一個給定的自旋系統, T1T_1T1? > T2T_2T2?
應用 (3.64)到(3.122) ,將旋轉坐標系下磁化矢量轉換到實驗室坐標系:
Mxy(t)=Mxy(0+)e?t/T2e?iω0tMz(t)=Mz0(1?e?t/T1)+Mz(0+)e?t/T1
\begin{align*}
M_{xy}(t) &= M_{xy}(0_+) e^{-t/T_2} e^{-i\omega_0 t} \tag {3.124a} \\
M_z(t) &= M_z^0 (1 - e^{-t/T_1}) + M_z(0_+) e^{-t/T_1} \tag {3.124b}
\end{align*}
Mxy?(t)Mz?(t)?=Mxy?(0+?)e?t/T2?e?iω0?t=Mz0?(1?e?t/T1?)+Mz?(0+?)e?t/T1??(3.124a)(3.124b)?
其中
Mxy(0+)=Mx′y′(0+)e?iω0τp(3.125)M_{xy}(0_+) = M_{x'y'}(0_+) e^{-i\omega_0 \tau_p} \tag {3.125}Mxy?(0+?)=Mx′y′?(0+?)e?iω0?τp?(3.125)
式(3.125)這是在實驗室坐標系中由信號檢測系統觀測到的“初始”橫向磁化分量的強度。包含時間延遲項是因為我們在脈沖結束時(t=τpt=\tau_pt=τp??,其中τp\tau_pτp?為脈沖持續時間)將時間重置為零,以便描述弛豫效應。
式(3.124)給出了射頻脈沖后橫向與縱向磁化強度隨時間演化的"精確"唯象描述。具體而言,從方程(3.124a)可明確看出:在實驗室坐標系中,橫向磁化強度的演化特征表現為指數衰減e?t/T2e^{-t/T_{2}}e?t/T2?和繞B0B_{0}B0?場的進動e?iw0te^{-iw_{0}t}e?iw0?t。自由進動周期的時長取決于T2T_{2}T2?值。對于生物組織而言,T2T_{2}T2?值通常在數十毫秒量級,這使得在此期間能夠檢測到磁共振信號。
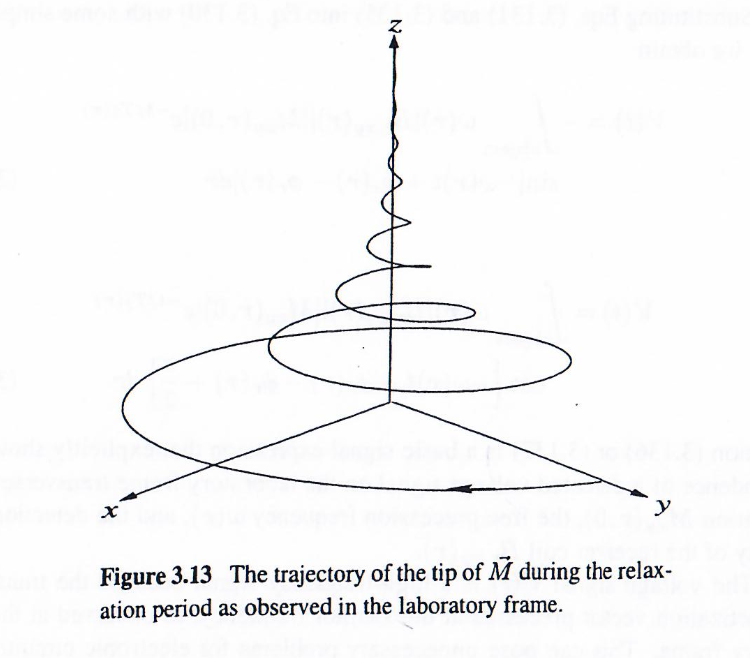
需要特別說明的是,當M?\vec{M}M因弛豫過程以螺旋運動方式”回歸“z軸時(如上圖所示),其模長并不守恒。該行為與激發期間M?\vec{M}M保持固定模長從z軸螺旋下行的運動特性存在本質區別。簡單的說,是因為:
- 射頻激發存在聚相的作用,這使得 z′z'z′ 軸宏觀磁化強分量 Mz′M_{z'}Mz′? “全都”轉換為 x′y′x'y'x′y′ 平面宏觀磁化強分量 Mx′y′M_{x'y'}Mx′y′?
- 弛豫過程中,聚相效果消失,因為失相,導致 x′y′x'y'x′y′ 平面宏觀磁化強分量 Mx′y′M_{x'y'}Mx′y′? 快速衰減(相互抵消),但是這部分抵消并不能轉化為 z′z'z′ 軸的宏觀磁化強分量 Mz′M_{z'}Mz′?,
- Mz′M_{z'}Mz′? 方向的恢復,實際上是高能級的原子躍遷回落到低能級
失相的唯象解釋(不是精確的量子力學角度的解釋):
- 不同原子所處微觀磁場環境不同,使得不同的原子的進動頻率略有不同
- 這使得原本相位同步的進動,開始慢慢分離,最后相互抵消,失相的過程請看下圖
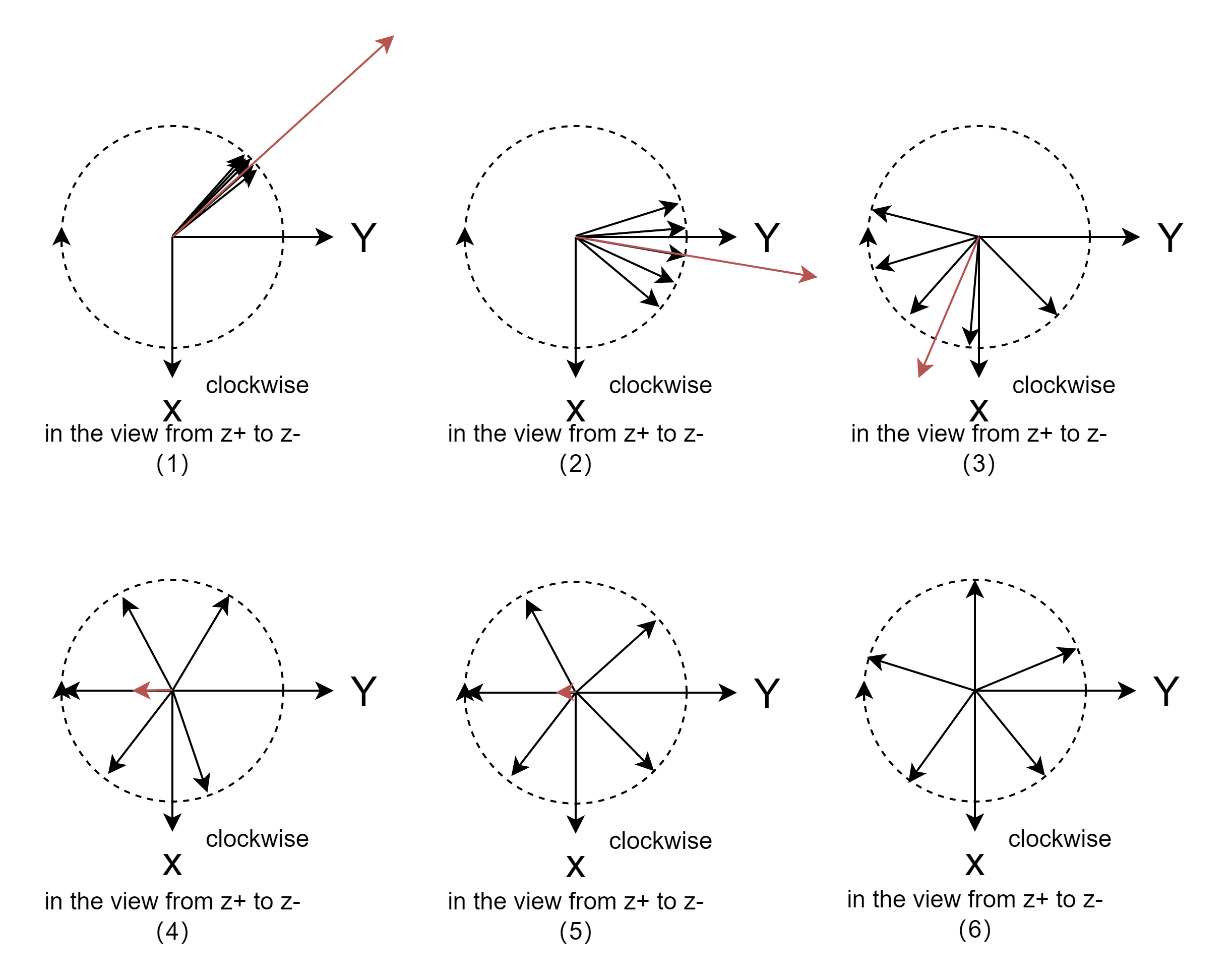
- 下圖是實驗室坐標下的 xyxyxy 平面,不同原子的磁矩 u?n\vec u_nun?的 xyxyxy 分量uxy,nu_{xy,n}uxy,n? (下圖黑線)和凈宏觀磁化矢量分量 MxyM_{xy}Mxy? (下圖紅線)
- 下圖1,射頻激發剛結束,不同原子的磁矩 u?n\vec u_nun? 的 xyxyxy 分量uxy,nu_{xy,n}uxy,n? 仍保持同相,其合成后的凈宏觀磁化矢量分量 MxyM_{xy}Mxy? 處于最大值,為Mxy(0+)M_{xy}(0_+)Mxy?(0+?)
- 下圖2,不同原子的磁矩 u?n\vec u_nun? 的 xyxyxy 分量uxy,nu_{xy,n}uxy,n? 因為進動頻率不同,在相同時間的旋轉角度不同,致使逐漸失去同相,他們的疊加后的MxyM_{xy}Mxy? 開始衰減
- 下圖3,4,5,是一個失相逐漸擴大的橫向弛豫過程
- 下圖6,弛豫完成,疊加后的凈宏觀磁化矢量分量MxyM_{xy}Mxy? 為0





,并在同一窗口顯示)











并測試腳本執行情況)

