基本思想

? ? ? ? 對于插入排序而言，它的基本思想就是往已經排好序的序列里邊插入數據。思想類似于玩撲克牌。接下來的排序都是基于下邊的這個數組。

int a[ ] = { 5 , 3 , 9 , 6 , 2 , 4 , 7 , 1 , 8 };

直接插入排序

? ? ? ? 我們想要將這個數組排成升序，在最一開始，我們可以認為數組的第一個元素5為一個有序的序列，5之后的元素就是一個個要往5這個有序的序列里邊插入的元素。

????????3顯然比5要小，要想排成升序，那么5就要移動到3的位置，3插入到5原來的位置。接下來的操作其實也是這樣的。

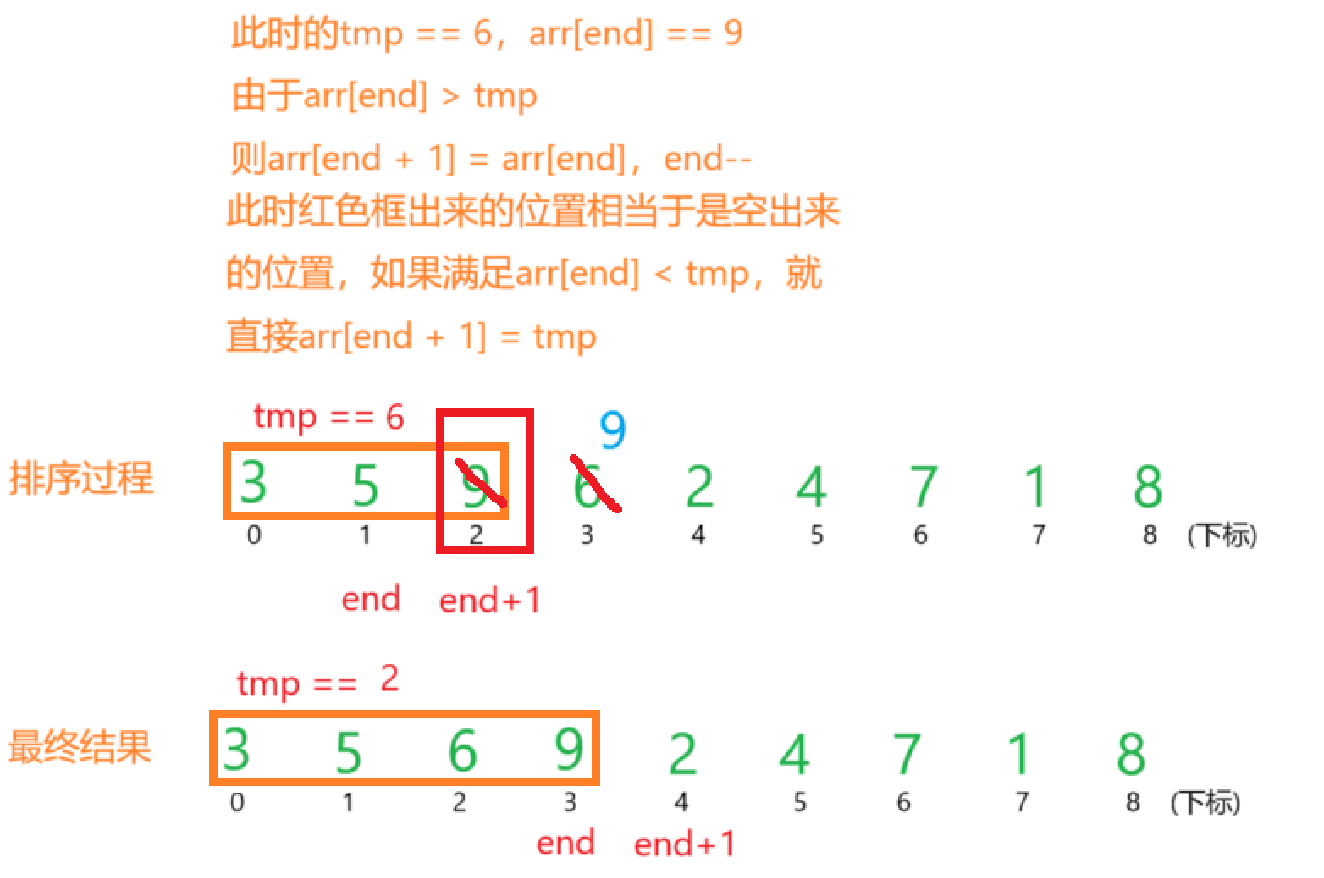
????????為了完成上邊的操作，我們需要一個變量tmp去存儲要插入的數據，我們還需要變量end去標記有序序列里邊的最后一個元素，那么end + 1就表示的是待排序序列里邊的第一個元素。

? ? ? ? 有了上邊的鋪墊，代碼的基本思路就出來了。拿end + 1位置的元素先給給tmp，接著拿end位置的元素與tmp做比較。如果arr[end] > tmp，就直接把arr[end + 1] = arr[end]，可是到這，tmp依舊沒有到它該去的有序的位置，所以end--，此時再重復上邊的過程，直到arr[end] < tmp，這時候把arr[end?+ 1] = tmp。

? ? ? ? 順著上邊的思路，大家再結合我下邊的圖片理解。

? ? ? ? 具體代碼

//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}

? ? ? ? 從具體的代碼里邊還需要注意幾點，一方面是arr[end] < tmp的時候，將arr[end + 1] = tmp，另一方面，如果tmp的大小比有序序列里邊都小，那么tmp這時候其實是去的0下標的位置，此時end < 0，所以統一把arr[end + 1] = tmp寫在循環外邊。還有最外邊的那個for循環，i < n - 1，因為如果i == n的時候，end + 1已經越界了。

直接插入排序的時間復雜度

? ? ? ? 直接插入排序是由兩個循環嵌套而成的，最終的時間復雜度可以理解為最深層那行代碼執行的次數，假設if條件永遠成立，這是最壞的情況。可以畫個大概的表格來理解。

end = i?????????執行次數

??????0? ? ? ? ?? ? ? 1

??????1? ? ? ? ? ? ? ?2

??????2? ? ? ? ? ? ? ?3

??????.? ? ? ? ? ? ? ? .

??????.? ? ? ? ? ? ? ? .

??????.? ? ? ? ? ? ? ? .

? ? n - 2? ? ? ? ? n - 1

? ? ? ? 最后用等差數列求和一下，然后按照大0表示法的條件，得出時間復雜度最差的情況為0(N^2)。當大的數據全在前邊，小的數據全在后邊才能滿足這一個情況。但如果這個數組有序(小的元素都在前邊，大的數據都在后邊)，那么時間復雜度就降為0(N)了。

? ? ? ? 為了滿足每次待排序的序列都可以滿足小的數據大都在前邊，大的數據大都在后邊，我們就需要采取一些優化的手段，希爾排序可以幫助我們。

希爾排序

? ? ? ? 希爾排序是直接插入排序的優化版本，它的基本思想就是將待排序序列先分組，組內先排序，最后大致滿足小的數據在前，大的數據在后了之后，再進行直接插入排序。

? ? ? ? 希爾排序法又叫縮小增量法，具體的實現就是先選定?個整數（通常是gap = n/3+1），把待排序序列所有記錄分成各組，所有的距離相等的記錄分在同?組內，并對每?組內的記錄進?排序，然后gap=gap/3+1得到下?個整數，再將數組分成各組，進?插?排序，當gap=1時，就相當于直接插?排序。gap為幾，就分為幾組。

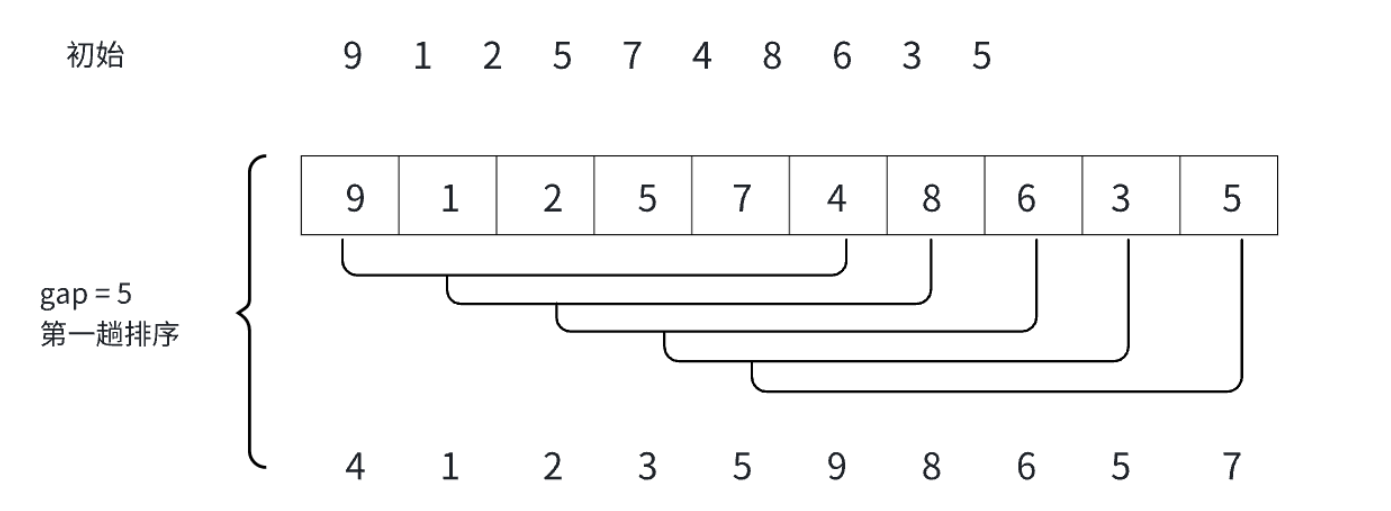
? ? ? ? 這就是完整的分組情況。

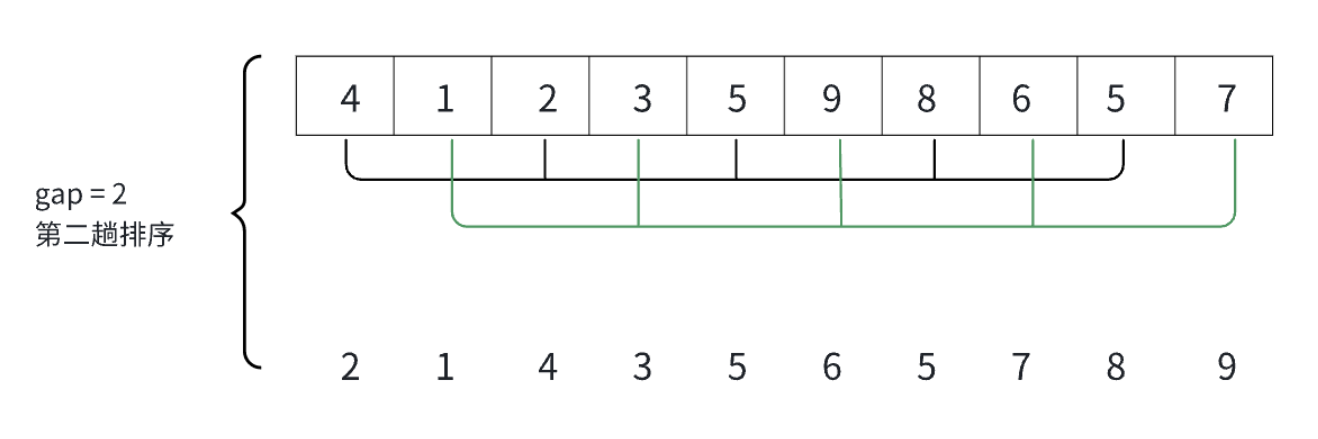
? ? ? ? 就拿gap == 2來具體說明。

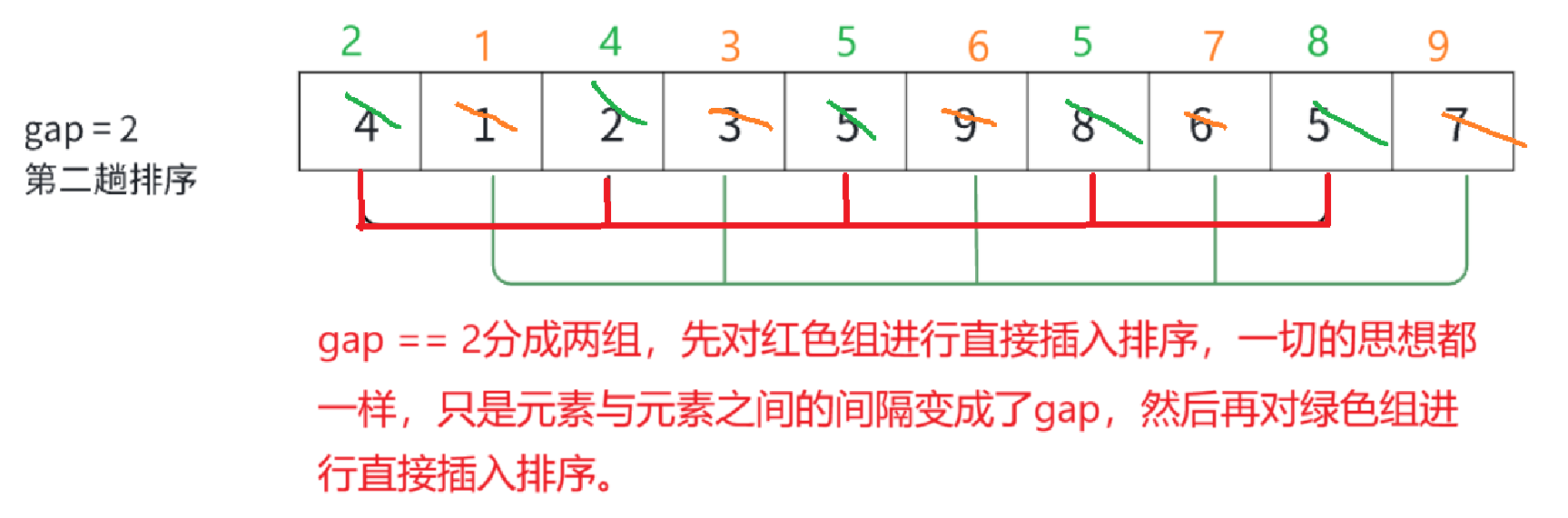
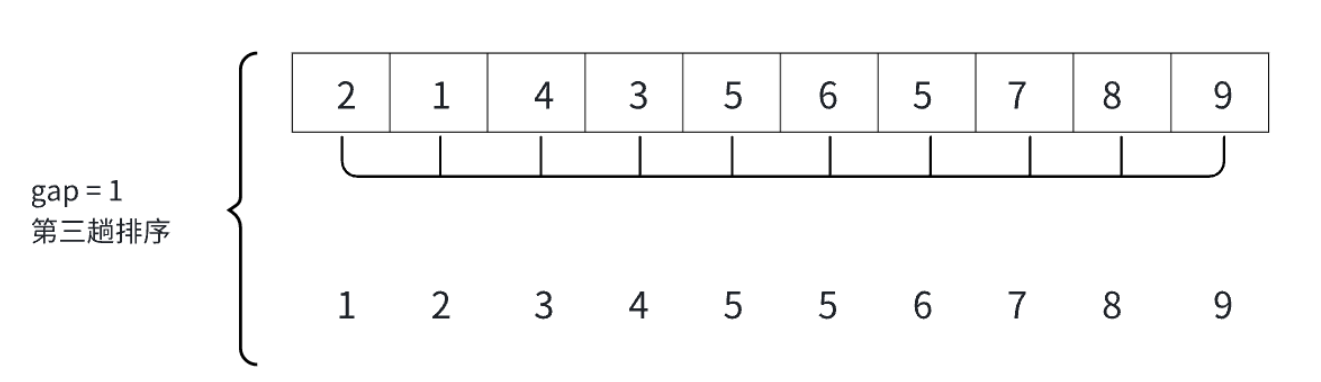
? ? ? ? 很直觀的可以看出，經過了兩次分組，并且組內排序之后，元素變成了我們最希望看到的樣字，小的全在前邊，大的都在后邊。

? ? ? ? 我們稱gap > 1為預排序，而gao == 1就為直接插入排序。這是一個優化的過程，本質還是直接插入排序，整體代碼變化不大。

????????代碼實現

//希爾排序
void ShellSort(int* arr, int n)
{int gap = n;while(gap > 1)//gap > 1都是預排序{gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = tmp;}}
}

? ? ? ? 對于最外層的while循環來說很好理解，因為循環里邊都是在進行預排序，所以要滿足gap > 1，除去for循環的循環條件不看，其他的代碼就是直接插入排序一樣的代碼，只不過是元素之間的距離變成了gap，對于for循環來說，為什么要i?< n - gap，是因為我們簡化了代碼，如果真的按照一組組去進行排序的話，就要再多嵌套了個循環了，這顯然不合適，所以我們就對各組同時進行直接插入排序。

? ? ? ? 還是拿gap == 2為例子(上邊有圖)，gap為2的時候總共分為兩組，i = 0的時候進入for循環就是在對紅色組進行排序，排序完，i++，再進入for循環，就是在對綠色組進行排序，以此類推，又由于每組之間的元素相差gap，所以當end == n - gap的時候已經是在最后一個元素的位置，再往下end + gap就越界了。

希爾排序的時間復雜度

? ? ? ? 希爾排序的復雜度是算不出來的，官方的給出的大致復雜度是0(N^1.3)，可見是比直接插入排序優化了不少。