打工人日報20250822

對自己負責，可以是換一個角度看待自己不喜歡的工作，轉換一個角度，從中找到自己感興趣的點
真的非常不想計算聲場的數據
啊啊啊啊啊

技術

STM32燒錄問題

STM32 代碼燒錄失敗：Error: Flash Download failed - Target DLL has been cancelled

vivado項目不要有中文路徑

QLCDNumber* lcdNumber

基本使用

// mainwindow.h
#ifndef MAINWINDOW_H
#define MAINWINDOW_H#include <QMainWindow>
#include <QLCDNumber>QT_BEGIN_NAMESPACE
namespace Ui { class MainWindow; }
QT_END_NAMESPACEclass MainWindow : public QMainWindow
{Q_OBJECTpublic:MainWindow(QWidget *parent = nullptr);~MainWindow();private:Ui::MainWindow *ui;QLCDNumber *lcdNumber;
};#endif // MAINWINDOW_H

// mainwindow.cpp
#include "mainwindow.h"
#include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow)
{ui->setupUi(this);// 創建 QLCDNumber 對象lcdNumber = new QLCDNumber(this);lcdNumber->setGeometry(50, 50, 200, 100); // 設置位置和大小lcdNumber->display(42); // 顯示初始數字
}MainWindow::~MainWindow()
{delete ui;
}

獲取和設置參數

獲取顯示的數字：可以使用 int value = lcdNumber->intValue(); 獲取當前顯示的整數值。
設置顯示的數字：除了使用 display(int num) 顯示整數外，還可以顯示其他類型的數據。
顯示浮點數：lcdNumber->display(double num);
顯示十六進制數：lcdNumber->display(QString::number(0x1F, 16));

// 在 MainWindow 類的某個槽函數中示例設置和獲取
void MainWindow::on_someButton_clicked()
{// 設置顯示的數字lcdNumber->display(123.45);// 獲取顯示的數字（如果是浮點數，需使用 doubleValue()）double currentValue = lcdNumber->doubleValue();qDebug() << "Current value:" << currentValue;
}

修改樣式

設置數字位數：使用 setDigitCount(int num) 來設置顯示的最大數字位數。
設置模式：可以設置為十進制（默認）、十六進制、八進制或二進制，使用 setMode(QLCDNumber::Mode mode)。例如，lcdNumber->setMode(QLCDNumber::Hex);
設置顏色：可以通過樣式表來修改顏色。

// 設置數字位數為 5 位
lcdNumber->setDigitCount(5);// 設置為十六進制模式
lcdNumber->setMode(QLCDNumber::Hex);// 使用樣式表修改背景色和數字顏色
lcdNumber->setStyleSheet("QLCDNumber { background-color: black; color: green; }");

擬合數據，記得計算R平方值，檢查擬合有效性

R平方（決定系數）是用于評估回歸模型擬合優度的統計量。它衡量了因變量（在你的例子中是聲功率）的總變異中可以由自變量（電壓）解釋的比例。
R平方的取值范圍在 0 到 1 之間。
R平方 =1表示模型完美擬合數據，即所有數據點都恰好位于回歸線上，所有的變異都能由模型解釋。
R平方 =0 則表示模型完全無法解釋因變量的變異，模型預測值等同于因變量的均值。通常，R平方越接近 1，說明模型對數據的擬合效果越好。但需要注意的是，增加自變量（特征）可能會使 R平方增大，即使這些自變量實際上對因變量沒有預測能力，所以在評估模型時，還需要結合其他指標，如調整后的 R平方 等。

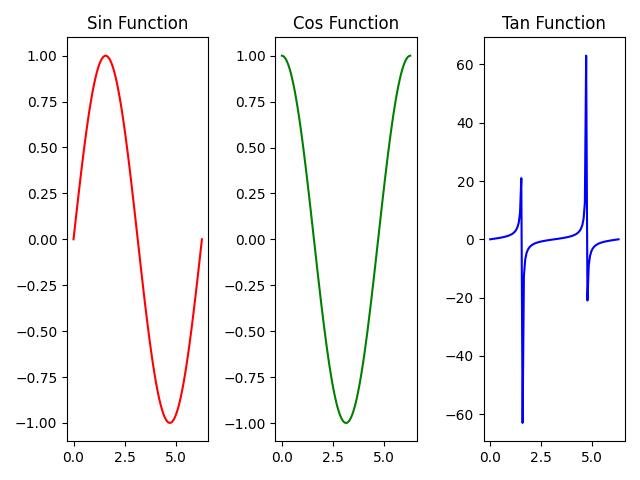
plt.subplot(1, 3, 1)行列熟悉

matplotlib 庫中用于在圖形中創建子圖的函數。它將圖形區域劃分為一個 1 行 3 列的網格布局，并選擇在第一個子圖位置進行繪圖操作。

import matplotlib.pyplot as plt
import numpy as np# 創建數據
x = np.linspace(0, 2 * np.pi, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.tan(x)# 創建 1 行 3 列的子圖布局，并選擇第一個子圖
plt.subplot(1, 3, 1)
plt.plot(x, y1, 'r')
plt.title('Sin Function')# 選擇第二個子圖
plt.subplot(1, 3, 2)
plt.plot(x, y2, 'g')
plt.title('Cos Function')# 選擇第三個子圖
plt.subplot(1, 3, 3)
plt.plot(x, y3, 'b')
plt.title('Tan Function')# 調整子圖之間的間距
plt.tight_layout()# 顯示圖形
plt.show()

數據處理

數據處理還是有考慮不周全，還是需要多想，盡可能考慮影響因素，哎，慢慢來吧

人際

今天算平穩度過，沒有什么沖突，大家都一般友好，因為沒有有記憶點的東西了

閱讀

《學會提問》
第五章 價值觀假設和描述性假設是什么
價值觀，假設是指一種想當然的想法，認為相互對立的價值觀當中的一個比另外一個更加的重要，比如說忠誠和誠實、競爭與合作、秩序和言論自由，理性和沖動；
描述性，假設是我們對世界過去未來現在所持有的信念價值觀，發現描述性假設的線索是不斷地思考理由和結論之間的鴻溝，找到支持理由的觀點，把自己放到對立面思考，以及對論題進一步的學習和了解
價值觀假設和描述性假設是連接結論和理由的隱形扣子，學會識別表達著的論證當中的價值觀假設和描述性假設，才可以更加全面的理解論證
記得在閱讀是要找到結論和支持結論的理由，尤其注意，當所以理由成立，并不代表結論就成立，需要找到其中的關系，確定理由是實實在在支持結論的，使結論成立的。

感恩

今天食堂的菜都比較喜歡，都要有選擇困難癥了，感謝食堂工作人員。