機器學習【十】neural network

? 系統梳理了機器學習與神經網絡的基礎知識，涵蓋理論、核心概念及代碼實踐。理論部分包括線性模型（向量表示、廣義線性模型）、分類與回歸的區別、梯度下降（批量/隨機/小批量）、激活函數（Sigmoid、ReLU等）、維度詛咒（特征數量與過擬合關系）、過擬合與欠擬合（誤差分析及處理方法）、正則化（L1/L2原理及差異）、數據增強（傳統與生成式手段）及數值穩定性（梯度消失/爆炸解決）。神經網絡核心涉及激活函數作用、模型復雜度與泛化平衡。代碼實踐部分通過線性模型梯度下降演示、不同優化策略對比、激活函數可視化、過擬合模擬及神經網絡（MNIST分類）構建，直觀展示理論應用。

1 線性模型

????????我們首先來回憶一下之前學習過的線性模型。給定n維輸入x = [x1,x2,...,xn]T，線性模型有一個n維權重和一個標量偏差 w = [w1.w2,....,wn]T, b。輸出是輸入的加權和 :

$y = w_{1} x_{1}+ w_{2} x_{2}+...+ w_{n} x_{n}+b$

轉換為向量版本就是?

$y = \left \langle w,x \right \rangle + b$

就像我們之前描述影響房價的關鍵因素是臥室個數，衛生間個數和居住面積記為x1,x2,x3。成交價是關鍵因素的加權和：

$y = w_{1} x_{1}+ w_{2} x_{2}+ w_{3} x_{3}+b$

除了直接讓模型預測值逼近實值標記 y，我們還可以讓它逼近 y 的衍生物，這就是廣義線性模型

$y =g^{-1}( w^{T} x + b)$

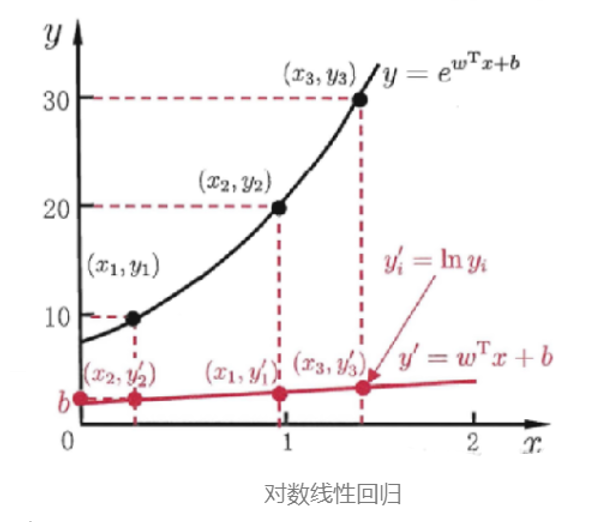
其中 ? $g^{-1}$ 稱為聯系函數（link function），要求單調可微。使用廣義線性模型我們可以實現強大的非線性函數映射功能。比方說對數線性回歸（log-linear regression），令

$ln y =w ^{T} x + b$

此時模型預測值對應的是真實值標記在指數尺度上的變化，如下圖所示。

2 分類與回歸

?我們再回顧到監督學習，監督學習分為回歸和分類。

監督學習	標簽	示例
回歸	用于標簽連續?	如何預測上海浦東的房價？
分類	用于標簽離散	根據腫瘤的體積、患者的年齡來判斷

線性模型的輸出可以是任意一個實值，也就是值域是連續的，因此可以天然用于做回歸問題。而分類問題的標記是離散值，怎么把這兩者聯系起來？

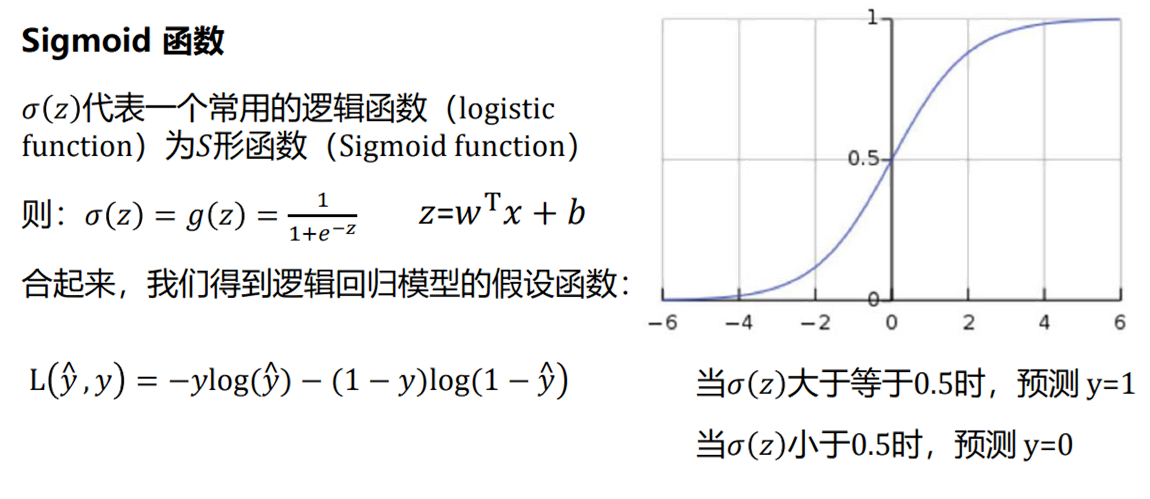
其實廣義線性模型已經給了我們答案，我們要做的就是：找到一個單調可微的聯系函數，把兩者聯系起來。對于一個二分類任務，比較理想的函數是單位階躍函數（unit_step function）:

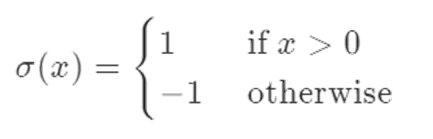
3 感知機模型

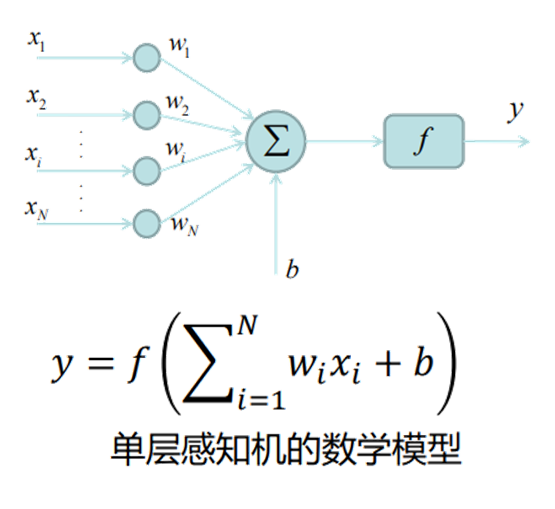
感知機是一種簡單的線性分類模型，主要用于解決二分類問題。它的核心思想是通過找到一個分離超平面，將特征空間中的正負兩類樣本點區分開來。
感知機的模型形式可以表示為：給定輸入特征向量 x，通過權重向量 w 和偏置 b 計算線性組合 w?x + b，然后根據這個結果的符號來判斷樣本類別。具體來說，當 w?x + b ≥ 0 時，將樣本判定為正類；當 w?x + b <0 時，判定為負類，可用符號函數表示為 f (x) = sign (w?x + b)。
感知機的學習過程就是求解合適的權重 w 和偏置 b 的過程，其目標是最小化分類錯誤。學習算法采用隨機梯度下降法，通過逐個處理誤分類樣本，不斷調整 w 和 b 的值：當樣本被誤分類時，根據錯誤情況對 w 和 b 進行更新，使超平面向誤分類樣本一側移動，逐漸減少誤分類的情況，直到沒有誤分類樣本為止。

這是對于感知機的一個簡單介紹，M.Minsky仔細分析了以感知機為代表的神經網絡的局限性，指出了感知機不能解決非線性問題。

1986年，Rumelhart和McClelland為首的科學家提出了BP(Back Propagation)神經網絡的概念，是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡，目前是使用最廣泛的神經網絡。

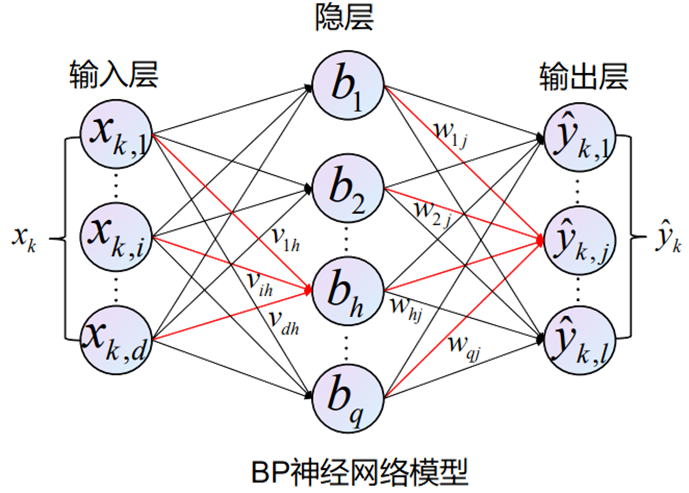
我們會收集一些數據點來決定模型的參數值（權重和偏差），例如過去6個月賣的房子。這被稱之為訓練數據。通常越多越好。

假設我們有n個樣本，記

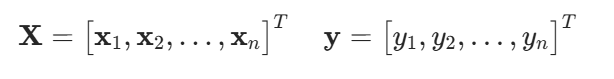
我們來比較真實值和我們預估的一個值，例如房屋售價和估價。假設Y是真實值， $\widehat{y}$ 是估計值，我們可以比較平方損失(該形式方便于后續微分)

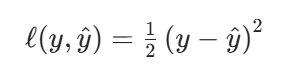
訓練損失：

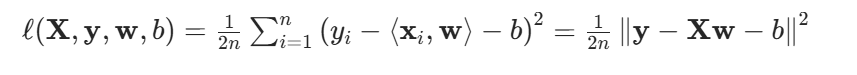
我們最小化損失來學習參數：

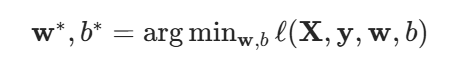
好的，接下來我們繼續介紹梯度下降：我們對于一個初始值 $w_{0}$ ,在重復迭代參數t = 1,2,3..

$w_{t} = w_{t-1} - \eta \frac{\delta t}{\delta w _{t-1} }$

沿梯度方向將增加損失函數值，而學習率就是步長的超參數。

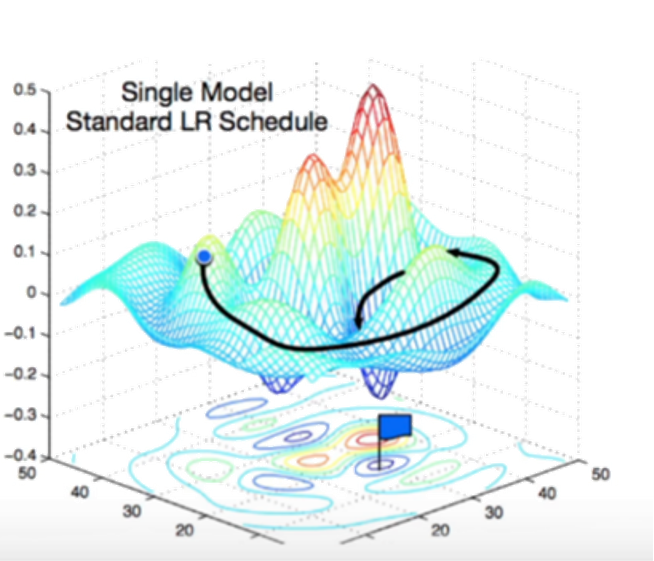
我們之所使用小批量隨機梯度下降，因為在整個訓練集上算梯度太貴，一個深度神經網絡模型可能需要數分鐘至數小時。

我們可以隨機采樣 b個樣本來近似損失

$\frac{1}{b}\sum L(X_{i},Y_{i},W)$

b是一個重要的超參數，表示批量大小。選擇一個合理的批量大小。不能太小，每次計算量太小，不適合并行來最大利用計算資源。也不能太大，內存消耗增加浪費計算，例如如果所有樣本都是相同的。

那么，模型是如何進行訓練和調參的呢？接下來我們學習模型的執行步驟：

step 1 :? 初始化神經網絡

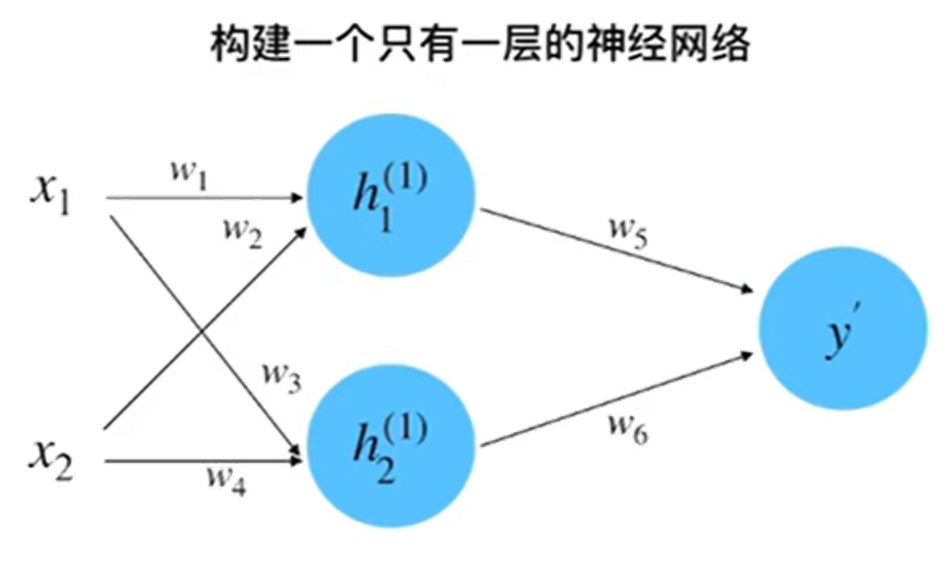
初始隨機賦值：x1 = 0.5,x2 = 1.0,y = 0.8,w1 = 1.0,w2 = 0.5,w3 = 0.5,w4 = 0.7,w5 = 1.0,w6 = 2.0

step 2 :? 前向計算

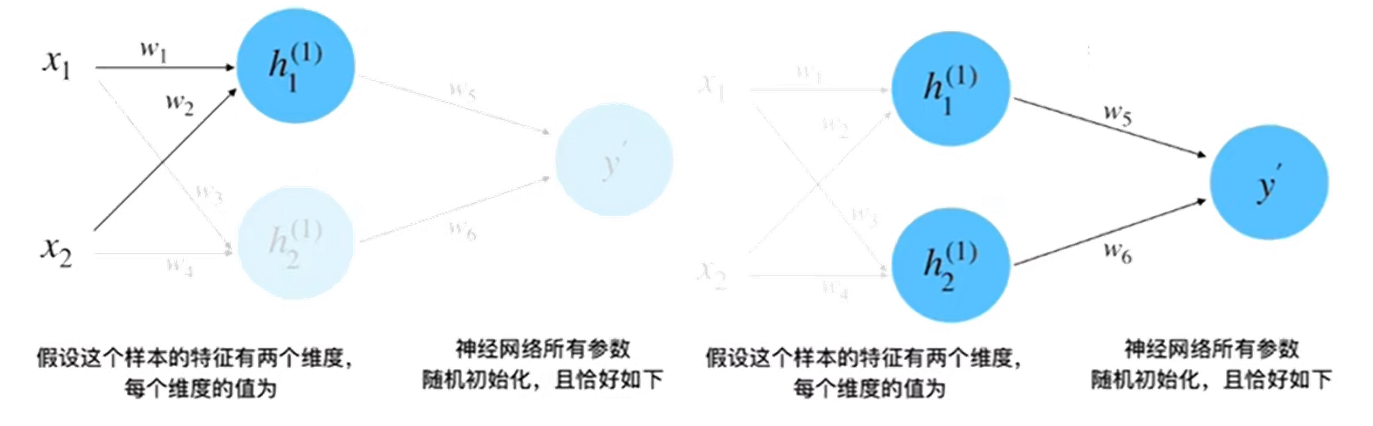參數賦值：x1 = 0.5,x2 = 1.0,y = 0.8,w1 = 1.0,w2 = 0.5,w3 = 0.5,w4 = 0.7,w5 = 1.0,w6 = 2.0

$h_{1}^{(1)} = w_{1}x_{1} + w_{2}x_{2}$ ?= 1.0 * 0.5 + 0.5 * 1.0 = 1.0 計算得到：

$h_{1}^{(1)} = 1.0$ ??? $h_{2}^{(1)} = 0.95$ ?繼而， ${y}' = w_{5}h_{1}^{(1)} + w_{6}h_{2}^{(1)}$ ?計算得到值為2.9

step 3 : 計算損失

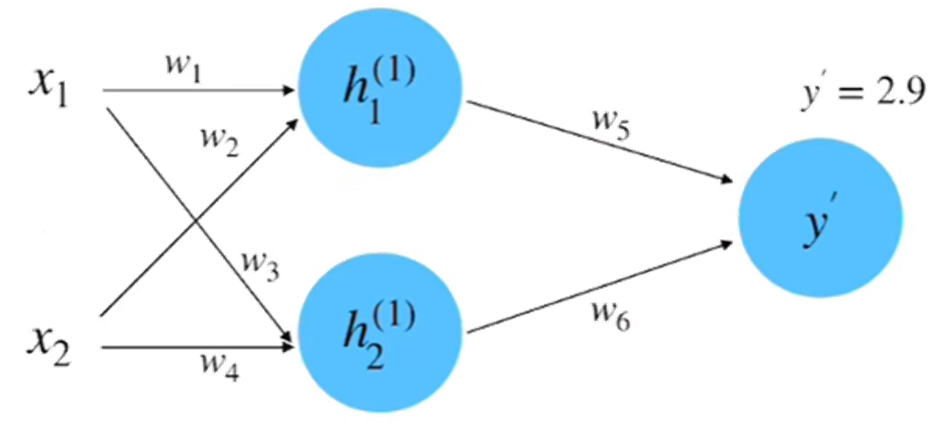
計算一下損失率： $\delta = \frac{1}{2}(y - {y}')^{2}$ ?得到結果為2.205

step 4 : 計算微分

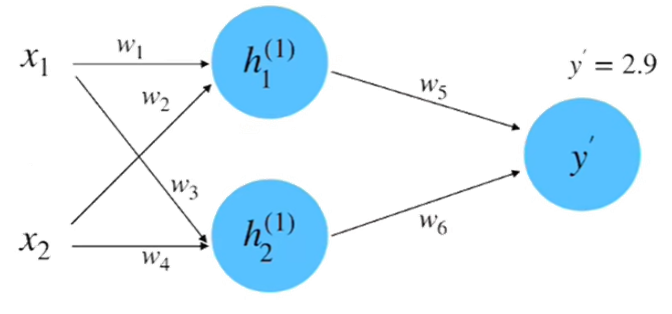
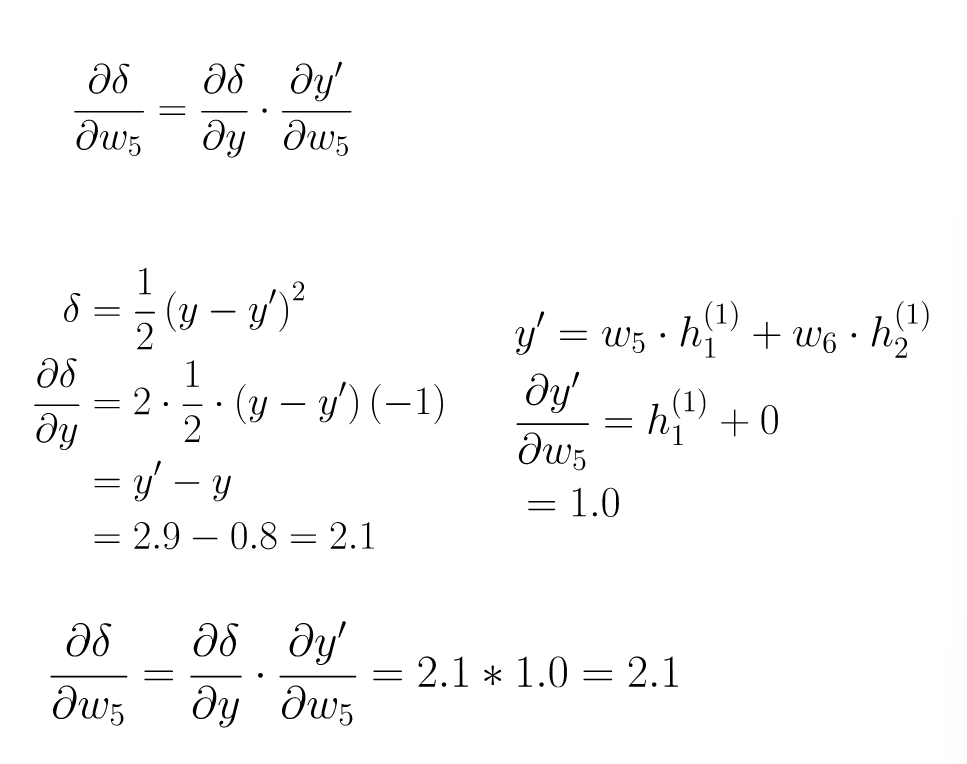
step 5 : 梯度下降

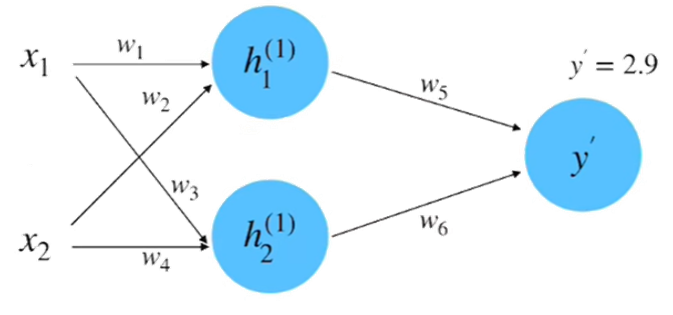
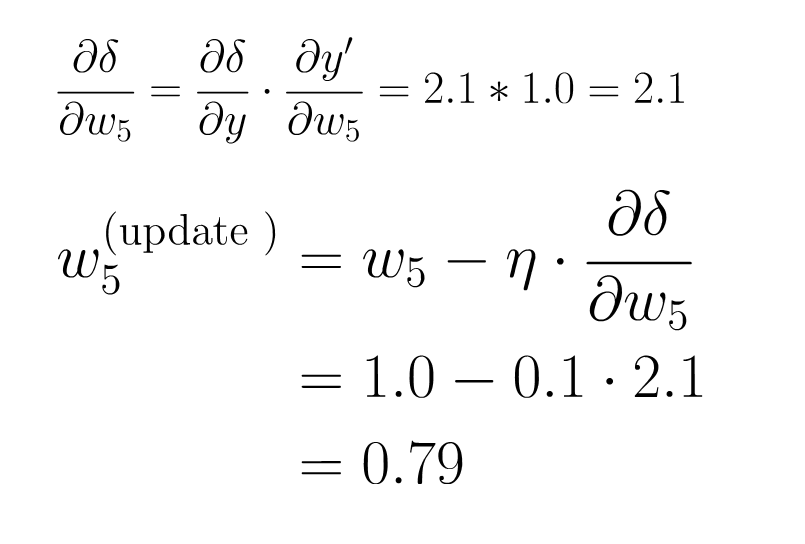
step6 : 反向傳播

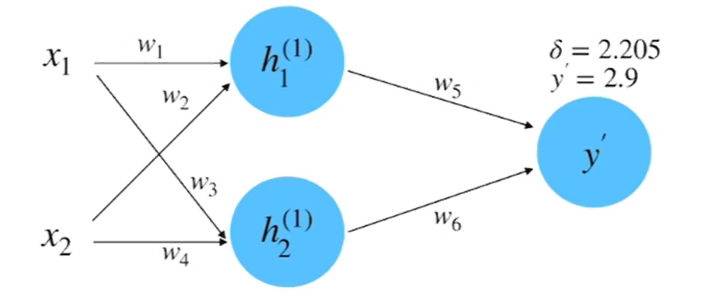
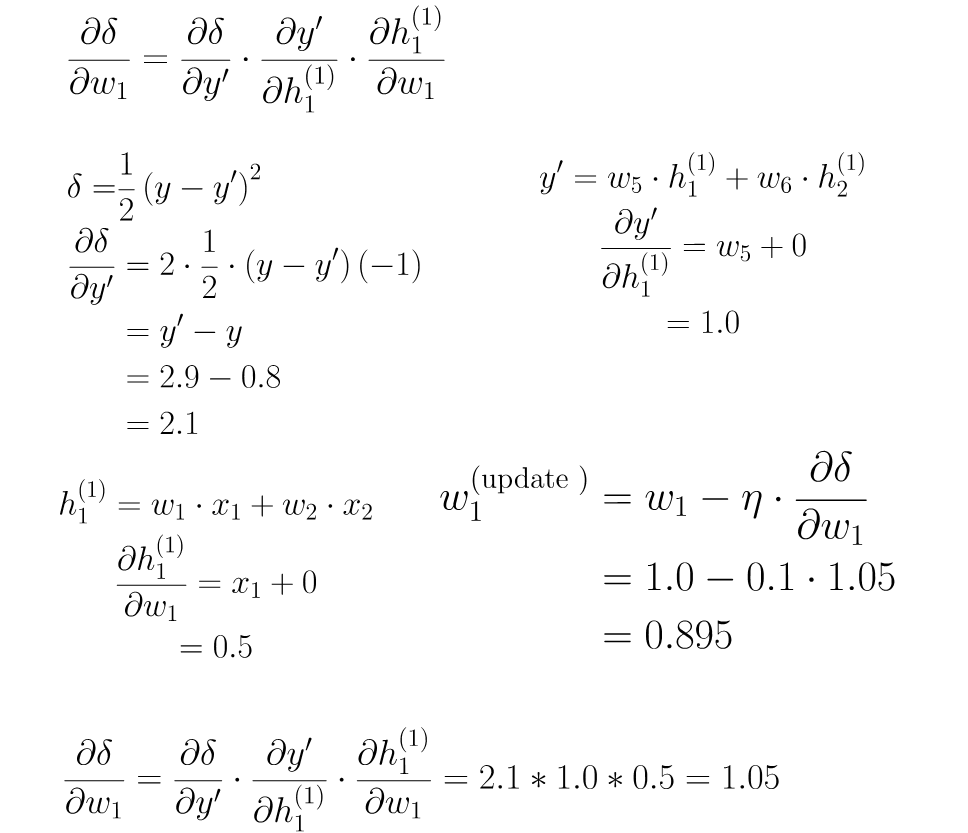
介紹完理論和公式，我們用擺攤煎餅果子的致富計劃來做一個通俗的解釋，便于我們理解：

你是一個夜市煎餅新手（神經網絡）。你的目標是攤出完美的煎餅（最小化損失函數）。你的老師傅會一直巡邏然后教導你（梯度下降），而顧客會以抽樣試吃團向你反饋（小批量樣本）。

??初攤災難：面糊炸鍋事件??

你開始對怎么攤煎餅果子一竅不通。初始配方（𝑤?=隨機參數）如下：

面粉500g+水1勺 → 直接面糊變水泥

醬料致死量 → 辣哭第一位顧客?

顧客給出差評：“煎餅像磚頭！醬料像噴火！”（損失值爆表）

?梯度下降：老師傅救場?

老師傅掂著鍋怒罵：

“你看看你這煎餅。誤差在哪？重點改三樣！”（計算梯度）

① ??醬太辣（誤差+80%）??→降辣度優先級MAX！

② ??面太厚（誤差+50%）??→減面粉次之

③ ??薄脆太少（誤差-10%）??→可忽略

?你開始按照師傅的建議進行配方的調整。而你調整的幅度就是?學習率η?

當η太大（猛降辣度80%）：新品甜如月餅 → 顧客掀攤：“我要吃煎餅不是點心！”

η太小（只降辣度1%）：繼續擺攤3個月仍被罵“噴火龍煎餅”

??設η=30%??：醬料減辣30%+面粉減20% → 有效減少誤差！

??小批量訓練：夜市速成法??

老師傅：“你這樣觀察100個客人太費時！還擺不擺攤了”（全量訓練費時）

你隨機抓 ??5個試吃員（b=5）??：

學生A：醬少點！

上班族B：多加薄脆！

大媽C：面糊稀些！

你就按照這些信息進行??批量調整??：醬少一點，薄脆多一點，面糊含水量再多一點。這樣就能夠讓80%客人滿意！

??批量大小b：地攤生存法則??

??b=1（只聽1人）??：學生說“多刷醬” → 狂加醬 → 大媽怒：“咸得發齁！”（過擬合）

??b=10（問卷普查）??：收10份需求時城管來了 → 攤沒了！（內存溢出）

??b=5（黃金值）??：多樣反饋+快速調整 → 出攤效率翻倍

??終極迭代：從地獄到米其林??

第1天：面糊水泥餅（損失值100）

第7天：老師傅舉喇叭循環播放：“往梯度反方向調！醬料誤差大就重點降醬！”

第30天：攤位排長隊——

“老板！照著你這參數（𝑤=最佳面粉比, 𝑏=黃金醬量）再來十套！”

名詞介紹??

① ??梯度下降?? = 老師傅罵你改配方：

??罵最狠的地方??（最大誤差）??優先改??

??罵多兇??（η）??決定你改多猛??

② ??小批量?? = 抓幾個路人試吃：用小樣本撬動大市場

③ ??批量b??：問太少→盲目，問太多→攤子癱瘓了

4 激活函數

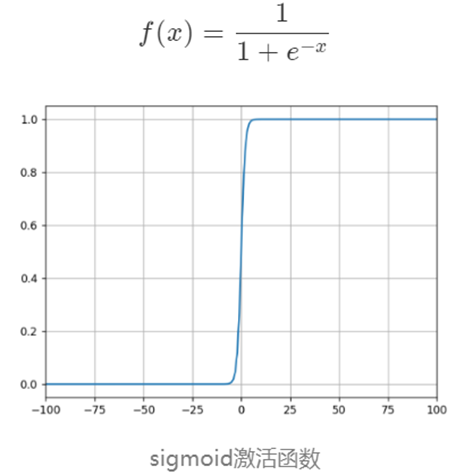
我們在深度學習中，一般習慣在每層神經網絡的計算結果送到下一層前都會添加一個激活函數。

激活函數是神經網絡的??非線性引擎??，通過動態調制神經元輸出與梯度流，使深度模型具備逼近復雜世界的表達能力。
??激活函數引入非線性??，破除線性模型的枷鎖。若無激活函數，無論疊加多少層，網絡僅能表達??線性變換??（等效于單層線性模型）。使神經網絡具備??逼近任意復雜函數??的能力（如圖像、語言等非線性數據），形成??深度學習的表達能力根基??。
???操作時接收上一層輸入的加權和（z = Σ(w_i·x_i) + b），通過函數?f(z)進行非線性轉換，輸出激活值?a至下一層。決定神經元是否被激活（如ReLU：正輸入激活，負輸入抑制）。

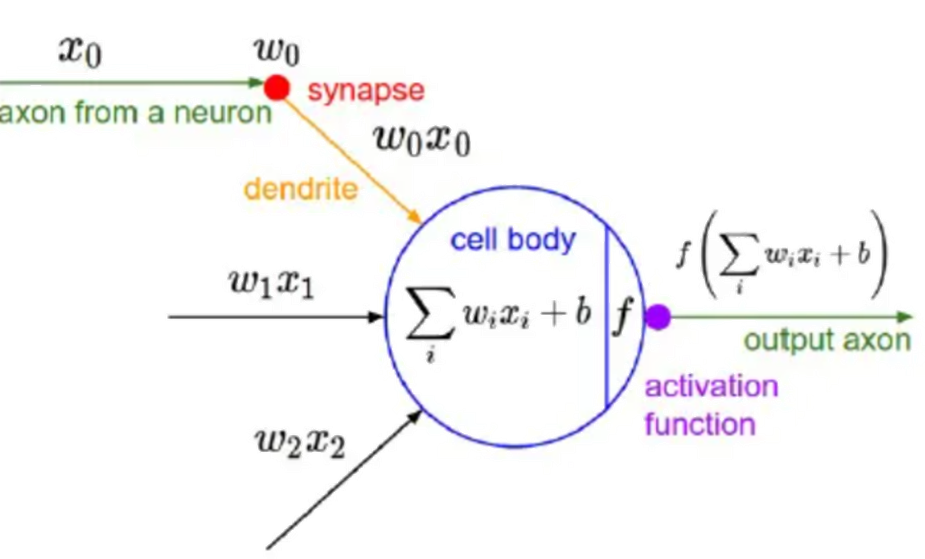
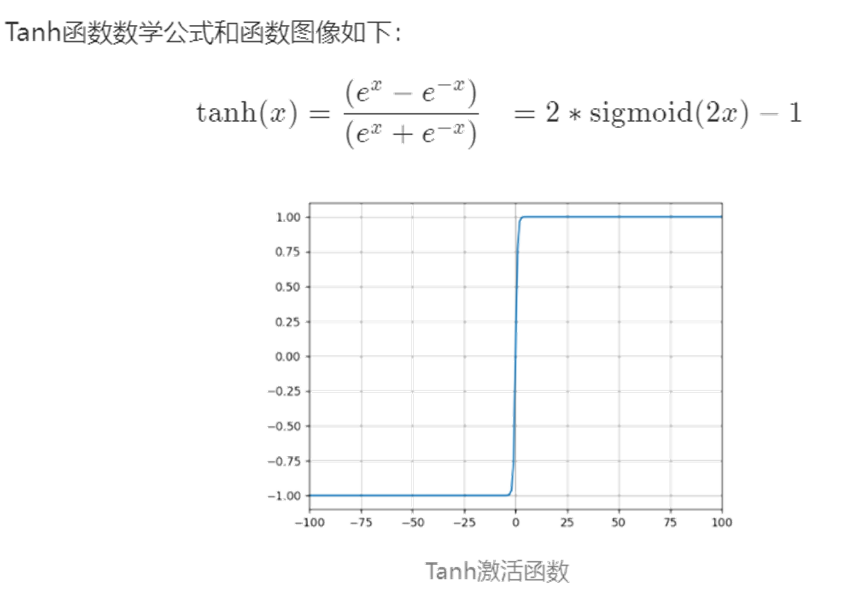
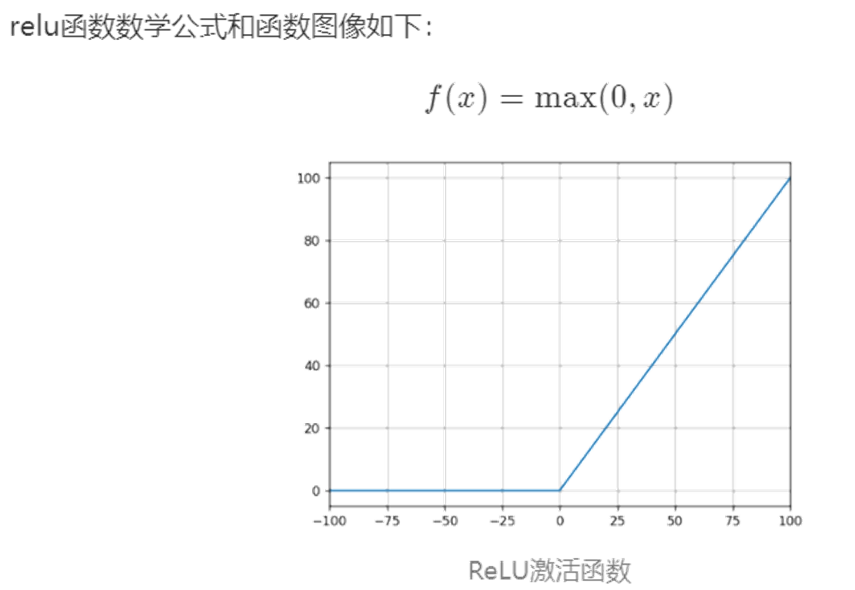
下面是幾種常用的激活函數和對應的圖像：

5 維度詛咒??

我們在進行分類問題的處理時，這里以貓狗分類為例：

??一維特征（如"圓眼睛"）??：由于貓狗均具備此特征，無法實現完美分類。

??二維特征（增加"尖耳朵"）??：在二維空間中數據開始分離，但仍存在重疊區域。

所以引入第三個特征（如"長鼻子"），構建??三維特征空間??：

數據分布更離散，可通過一個??分類超平面??（如綠色平面）有效區分貓狗。

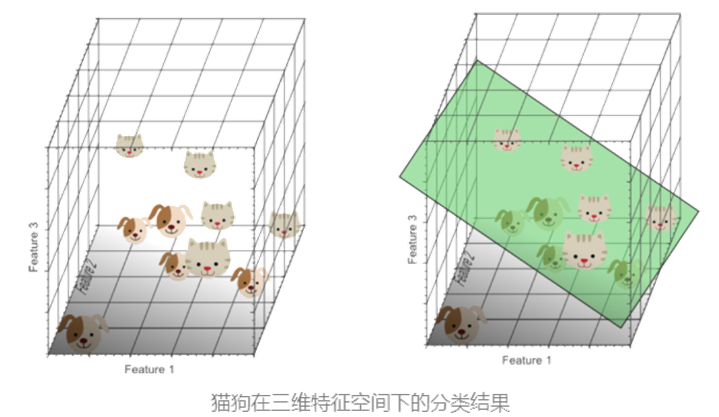
此時模型在一個高維度下能擬合更復雜的決策邊界，分類效果提升。?

我們在持續增加特征數量時，問題也會凸顯：

??當樣本密度指數級下降??：特征空間維數越高，數據分布越稀疏。

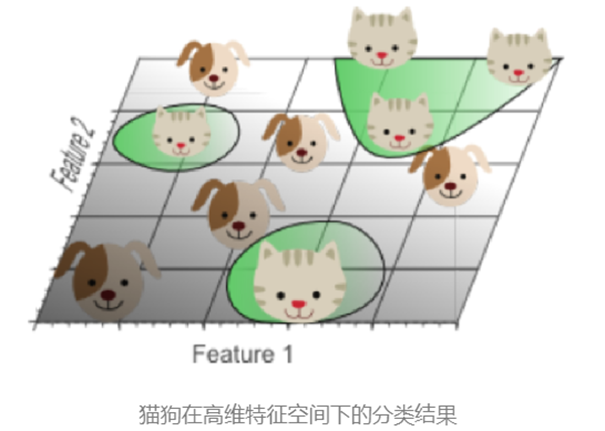
??這樣的稀疏性使找到"完美"分類超平面變得容易，但這是一種假象。此時在訓練集上的效果太好了，而訓練集不可能完全反應顯示現實生活，無法代表真實世界復雜性。這就是過擬合。

??過擬合的本質??是高維分類結果映射回低維時，決策邊界扭曲復雜，無法泛化到真實數據。

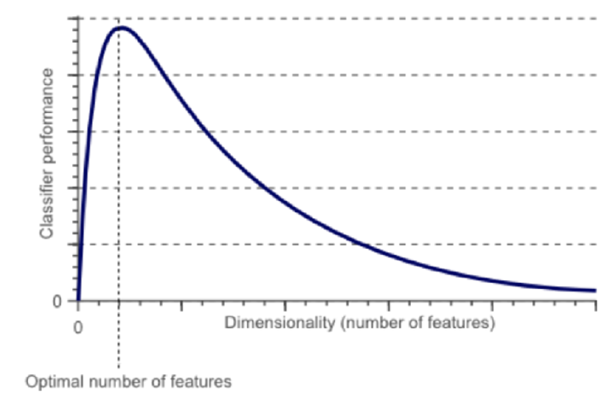
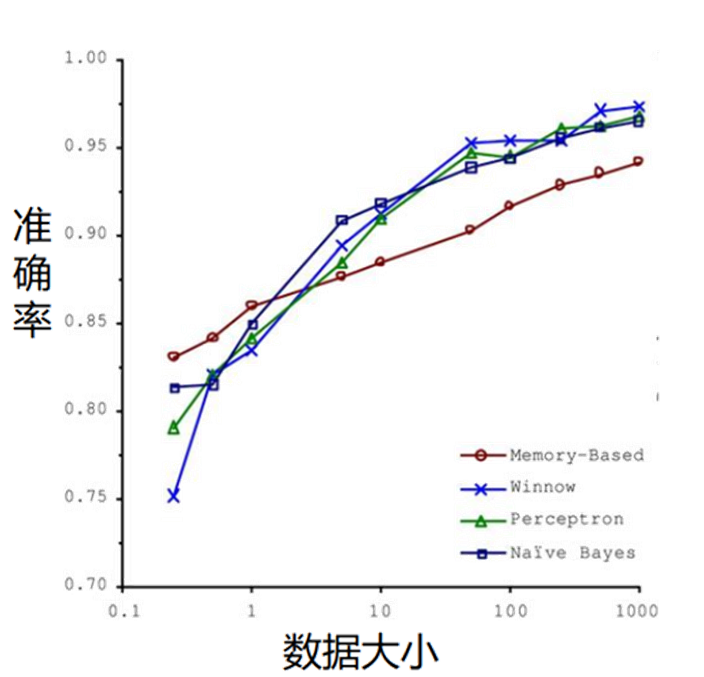
如圖像所示，隨特征數量增加，??分類性能先上升后下降??，存在最優特征數量閾值。

維度詛咒揭示了特征工程中的關鍵權衡——??適當增加特征可提升模型能力，但盲目追求高維會導致過擬合??。合理控制特征數量與復雜度，是規避詛咒的核心策略。（神經網絡的隱藏層其實就是在做數據的升降維。）

6 過擬合與欠擬合

剛剛我們提到了過擬合，而影響模型過擬合或者欠擬合的原因注意有兩個：數據（數據量多少）和模型容量（模型復雜度）

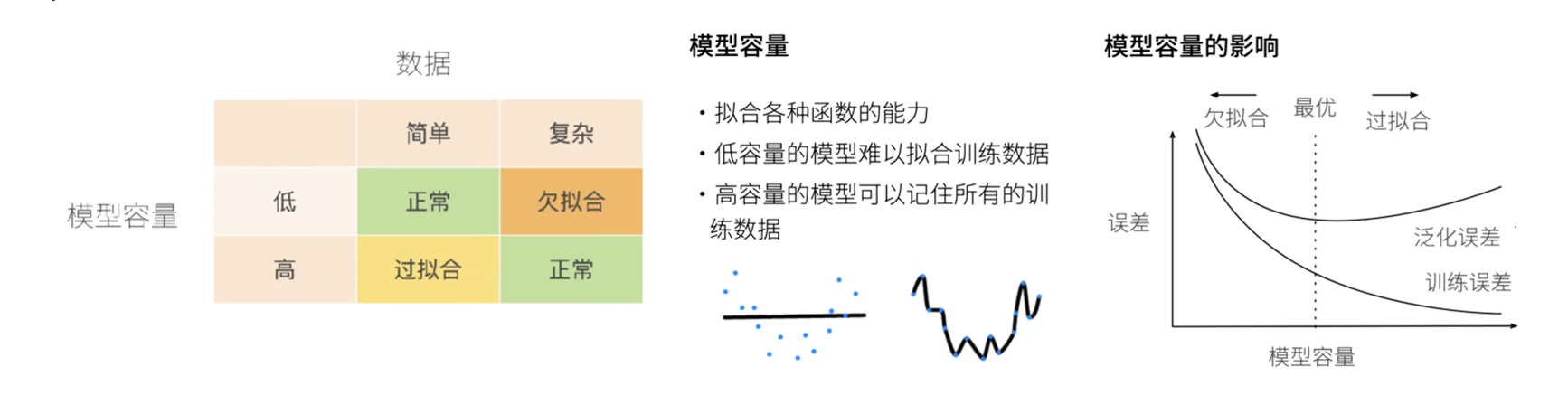??訓練誤差??：模型在訓練數據集上的誤差。

??泛化誤差??：模型在無限多真實分布數據上誤差的期望（實際通過獨立測試集估計）。

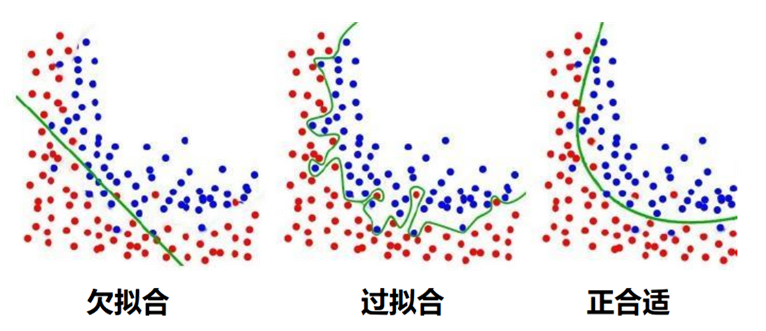
??過擬合??：訓練誤差極小，但泛化誤差大（模型過度學習訓練噪聲）。

??欠擬合??：訓練誤差與泛化誤差均大（模型未能捕捉數據規律）。

??目標??：同時降低訓練與泛化誤差，避免兩種現象影響模型泛化能力。

??過擬合的處理方法?

??正則化?	減少參數規模（如L1/L2正則化），約束模型復雜度。
??數據增強?	增加數據數量、質量或難度（如翻轉、裁剪圖像）。
??降維?	丟棄無關特征（手動選擇或算法如PCA）。
??集成學習?	?融合多個模型（如Bagging/Boosting），降低單模型過擬合風險。

欠擬合的處理方法?

??添加新特征?	挖掘組合特征，強化特征與標簽相關性。
??增加模型復雜度?	線性模型添加高次項；神經網絡擴展層數/神經元。
??減小正則化系數?	降低正則化強度（如減少λ值），釋放模型學習能力。

??過擬合需抑制模型復雜度??（正則化、數據擴充），??欠擬合需提升模型能力??（特征/復雜度增強）。

始終以降低泛化誤差為目標，平衡模型復雜性與數據特征表達力。

7 正則

深度學習中正則可視為通過約束模型復雜度來防止過擬合的手段。模型復雜度由參數量大小和參數取值范圍共同決定，因此正則分為兩個方向：

約束模型參數量（如 Dropout）
約束模型參數的取值范圍（如 weight decay）

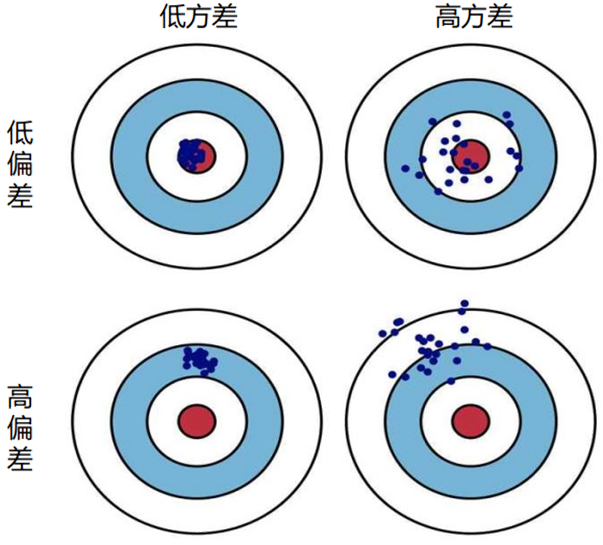
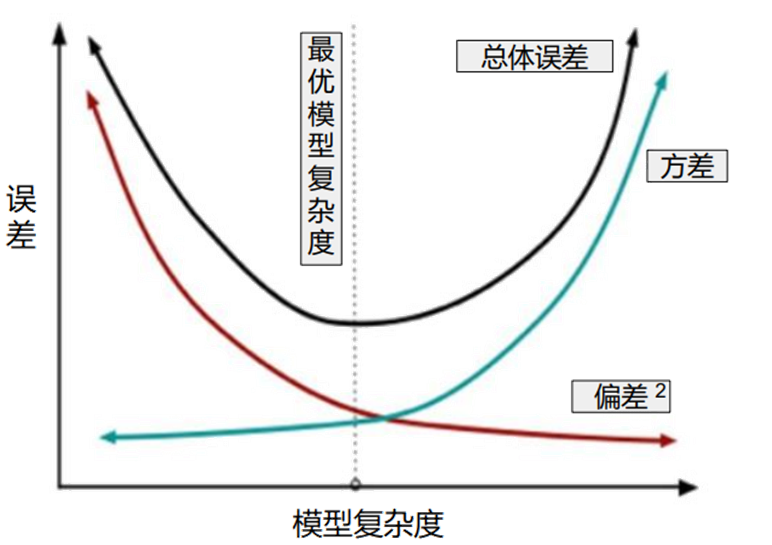
??偏差-方差權衡??

隨著模型復雜度增加，方差會??逐漸增大（模型對噪聲敏感）。偏差??逐漸減小（模型擬合能力增強）。正則化的核心是在虛線位置（模型復雜度適中）找到平衡點，使偏差和方差均適度，實現“適度擬合”。

??L1 與 L2 正則化的區別??

??L2 正則化??：
約束參數向原點靠近，使解更平滑。
??L1 正則化??：
約束解靠近某些坐標軸，同時使部分參數為零，產生稀疏解。

8 數據增強?

數據增強是通過??擴充訓練集容量??防止過擬合（與正則化互補）。

解決模型在數據量不足時過度依賴訓練樣本的問題。

??數據量增強??：

對現有樣本進行??簡單變換??生成新樣本（如旋轉、翻轉、裁剪、縮放、添加噪聲）。

示例：圖像數據通過旋轉90°生成新訓練樣本（需保持標簽有效性）。

??數據質量增強??：

提升數據信息密度（如文本數據清洗、圖像分辨率增強）。

??現代擴展??

??生成對抗網絡（GAN）??：

利用神經網絡生成??逼真新樣本??（如生成符合訓練集分布的圖像）。

實驗驗證可有效擴充數據集并提升泛化能力。

??關鍵結論??

??"成功的機器學習應用不是擁有最好的算法，而是擁有最多的數據！"???

方向	具體手段	作用
??傳統增強??	旋轉/翻轉/裁剪/加噪	低成本擴展數據量
??生成式增強??	GAN生成合成數據	解決小樣本問題
??本質目標??	突破訓練數據有限性	使模型適應真實世界復雜性

9 數值穩定性

這種數值不穩定性問題再深度學習訓練過程中被稱作梯度消失和梯度爆炸。

梯度消失：由于累乘導致的梯度接近0的現象，此時訓練沒有進展。

梯度爆炸：由于累乘導致計算結果超出數據類型能記錄的數據范圍，導致報錯。

防止出現數值不穩定原因的方法是進行數據歸一化處理。

10 代碼實現

?10.1 線性模型與梯度下降演示

# 線性模型與梯度下降演示import numpy as np
import matplotlib
import matplotlib.pyplot as pltmatplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# 隨機種子
np.random.seed(42)# 模擬數據
x = np.random.rand(100, 1) * 10  # 100個樣本，1維特征
y = 3 * x + 2 + np.random.randn(100, 1) * 2  # 真實值# 初始化參數
w = np.random.randn(1)  # 權重
b = np.random.randn(1)  # 偏置
lr = 0.0001  # 學習率
epochs = 1000  # 迭代次數# 梯度下降訓練
loss_history = []for epoch in range(epochs):# 前向計算y_pred = w * x + b# 計算損失loss = np.mean((y_pred - y)**2)loss_history.append(loss)# 計算梯度dw = 2 * np.mean((y_pred - y) * x)  # w的梯度db = 2 * np.mean(y_pred - y)       # b的梯度# 參數更新w -= lr * dwb -= lr * db# 輸出結果
print(f"訓練后參數：w={w[0]:.4f}, b={b[0]:.4f}")# 繪制損失曲線
plt.figure(figsize=(8, 4))
plt.plot(range(epochs),loss_history,color='tab:blue', linewidth=1.5)
plt.xlabel("迭代次數")
plt.ylabel("平方損失")
plt.title("梯度下降收斂過程")
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()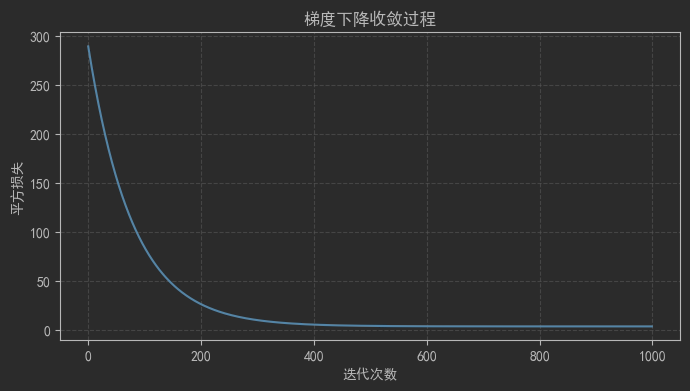

10.2 對比梯度下降的收斂速度

def bgd(x, y, lr=0.01, epochs=100):"""批量梯度下降"""# 初始化參數（w形狀為(1,1)，b形狀為(1,1)）w, b = np.random.randn(1, 1), np.random.randn(1, 1)n = len(x)  # 樣本數量（n=100）loss = []for _ in range(epochs):# 前向傳播：x形狀(100,1)，w形狀(1,1)，結果形狀(100,1)y_pred = x.dot(w) + b# 計算誤差（形狀(100,1)）error = y_pred - y# 計算梯度（x.T形狀(1,100)，與error點積后得到(1,1)的梯度）dw = (2/n) * x.T.dot(error)  # 形狀(1,1)db = (2/n) * np.sum(error)   # 標量（形狀()）# 參數更新（w和b形狀匹配）w -= lr * dwb -= lr * db# 記錄當前參數下全量數據的MSE損失（形狀()）loss.append(np.mean(error**2))return lossdef sgd(x, y, lr=0.01, epochs=100):"""隨機梯度下降"""# 初始化參數（w形狀(1,1)，b形狀(1,1)）w, b = np.random.randn(1, 1), np.random.randn(1, 1)n = len(x)loss = []for _ in range(epochs):# 隨機選擇1個樣本（索引范圍0~99）idx = np.random.randint(n)# 提取單樣本并保持二維形狀（避免一維廣播問題）xi = x[idx].reshape(1, 1)  # 形狀(1,1)yi = y[idx].reshape(1, 1)  # 形狀(1,1)# 前向傳播（單樣本預測值，形狀(1,1)）y_pred = xi.dot(w) + b# 計算單樣本誤差（形狀(1,1)）error = y_pred - yi# 計算單樣本梯度（形狀(1,1)）dw = 2 * error * xi  # 形狀(1,1)db = 2 * error       # 標量（形狀()）# 參數更新（w和b形狀匹配）w -= lr * dwb -= lr * db# 計算全量數據的MSE損失（使用當前參數預測所有樣本）y_pred_full = x.dot(w) + b  # 形狀(100,1)loss.append(np.mean((y_pred_full - y)**2))  # 標量return lossdef mbgd(x, y, lr=0.01, epochs=100, batch_size=10):"""小批量梯度下降"""# 初始化參數（w形狀(1,1)，b形狀(1,1)）w, b = np.random.randn(1, 1), np.random.randn(1, 1)n = len(x)loss = []for _ in range(epochs):# 隨機選擇batch_size個樣本（不重復）idx = np.random.choice(n, batch_size, replace=False)# 提取批量數據并保持二維形狀（形狀(batch_size,1)）xi = x[idx].reshape(batch_size, 1)yi = y[idx].reshape(batch_size, 1)# 前向傳播（批量預測值，形狀(batch_size,1)）y_pred = xi.dot(w) + b# 計算批量誤差（形狀(batch_size,1)）error = y_pred - yi# 計算批量梯度（xi.T形狀(1,batch_size)，與error點積后得到(1,1)的梯度）dw = (2/batch_size) * xi.T.dot(error)  # 形狀(1,1)db = (2/batch_size) * np.sum(error)    # 標量（形狀()）# 參數更新（w和b形狀匹配）w -= lr * dwb -= lr * db# 計算全量數據的MSE損失（使用當前參數預測所有樣本）y_pred_full = x.dot(w) + b  # 形狀(100,1)loss.append(np.mean((y_pred_full - y)**2))  # 標量return loss# 生成線性關系數據（y = 3x + 2 + 噪聲）
np.random.seed(42)
x = np.random.rand(100, 1) * 10  # 100個樣本，1個特征，形狀(100,1)
y = 3 * x + 2 + np.random.randn(100, 1) * 1.5  # 真實標簽，形狀(100,1)# 運行三種梯度下降（確保返回的loss長度均為100）
bgd_loss = bgd(x, y, lr=0.001, epochs=100)
sgd_loss = sgd(x, y, lr=0.0005, epochs=100)  # SGD學習率更小
mbgd_loss = mbgd(x, y, lr=0.001, epochs=100, batch_size=10)# 繪制收斂曲線（確保x和y長度一致）
plt.figure(figsize=(10, 6))
plt.plot(range(100), bgd_loss, label='批量梯度下降 (BGD)')
plt.plot(range(100), sgd_loss, label='隨機梯度下降 (SGD)')
plt.plot(range(100), mbgd_loss, label='小批量梯度下降 (MBGD)')
plt.xlabel('迭代次數')
plt.ylabel('均方誤差 (MSE)')
plt.title('不同梯度下降策略收斂速度對比')
plt.legend()
plt.grid(True)
plt.show()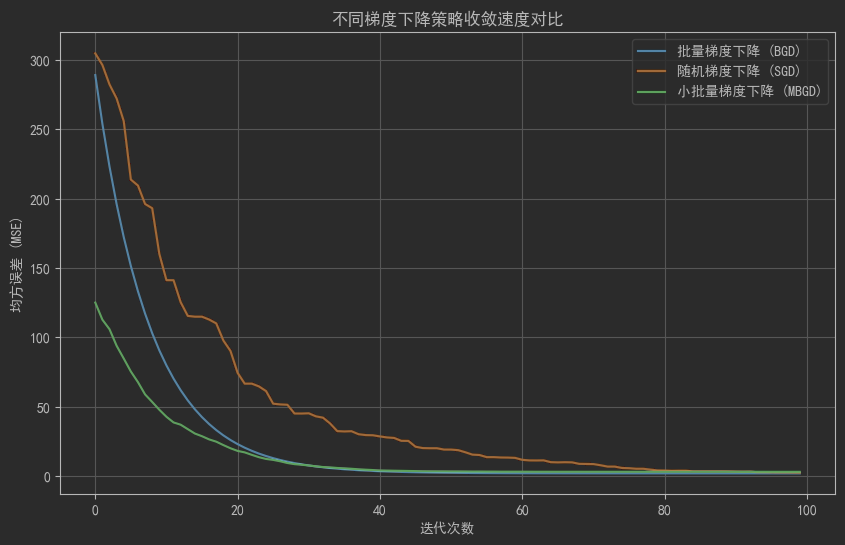

10.3 激活函數以及圖像

# 激活函數可視化# 定義激活函數
def sigmoid(x):return 1 / (1 + np.exp(-x))def tanh(x):return np.tanh(x)def relu(x):return np.maximum(0, x)def leaky_relu(x, alpha=0.1):return np.where(x > 0, x, alpha * x)# 生成輸入數據
x = np.linspace(-5, 5, 100)# 繪制圖像
plt.figure(figsize=(12, 8))plt.subplot(2, 2, 1)
plt.plot(x, sigmoid(x))
plt.title('Sigmoid')
plt.grid()plt.subplot(2, 2, 2)
plt.plot(x, tanh(x))
plt.title('Tanh')
plt.grid()plt.subplot(2, 2, 3)
plt.plot(x, relu(x))
plt.title('ReLU')
plt.grid()plt.subplot(2, 2, 4)
plt.plot(x, leaky_relu(x))
plt.title('Leaky ReLU')
plt.grid()plt.tight_layout()
plt.show()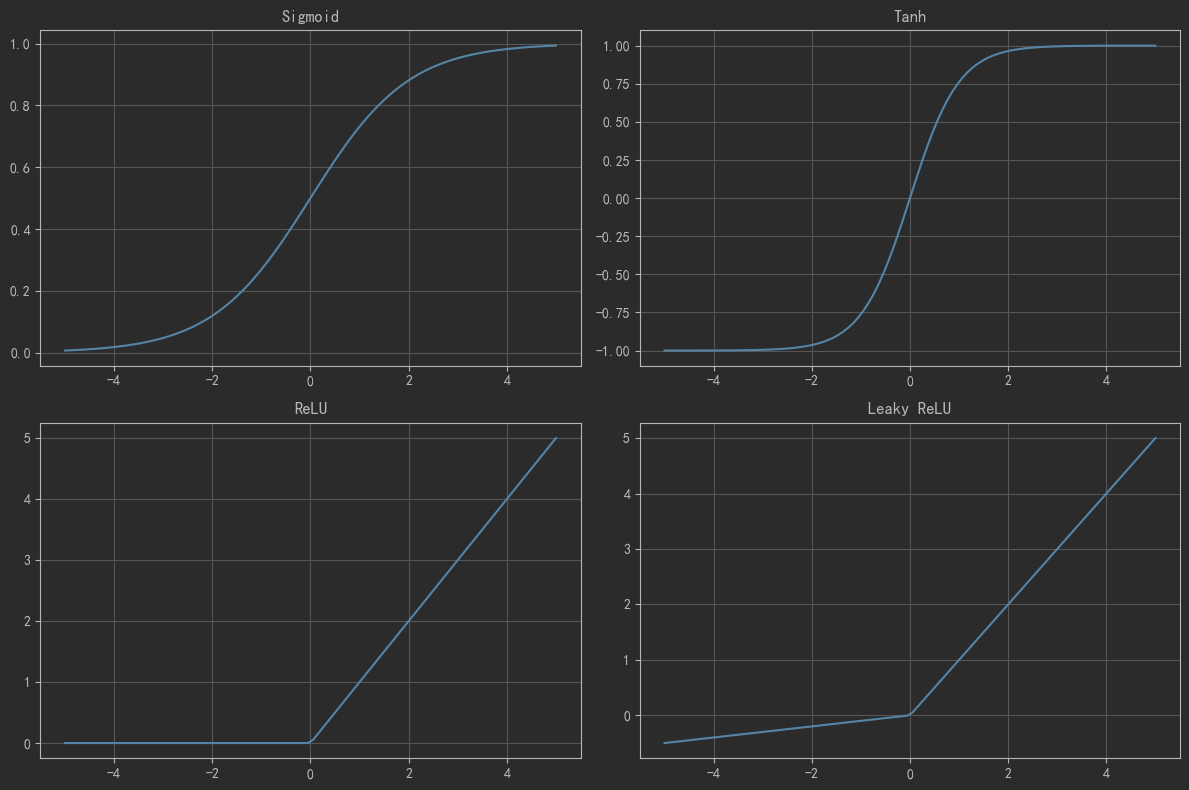

10.4 過擬合與欠擬合

# 過擬合與欠擬合演示from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split# 生成模擬數據
np.random.seed(42)
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x) + np.random.randn(100) * 0.1
x = x.reshape(-1, 1)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=42)# 定義不同階數的多項式模型
degrees = [1, 3, 5, 10, 15]
train_errors = []
test_errors = []for degree in degrees:# 構建多項式回歸模型model = make_pipeline(PolynomialFeatures(degree=degree),LinearRegression())model.fit(x_train, y_train)# 計算訓練和測試誤差y_train_pred = model.predict(x_train)y_test_pred = model.predict(x_test)train_errors.append(np.mean((y_train_pred - y_train)**2))test_errors.append(np.mean((y_test_pred - y_test)**2))# 繪制誤差曲線
plt.figure(figsize=(10, 6))
plt.plot(degrees, train_errors, 'o-', label='訓練誤差')
plt.plot(degrees, test_errors, 'o-', label='測試誤差')
plt.xlabel('多項式階數（模型復雜度）')
plt.ylabel('均方誤差')
plt.title('過擬合與欠擬合：模型復雜度 vs 誤差')
plt.xticks(degrees)
plt.legend()
plt.grid()
plt.show()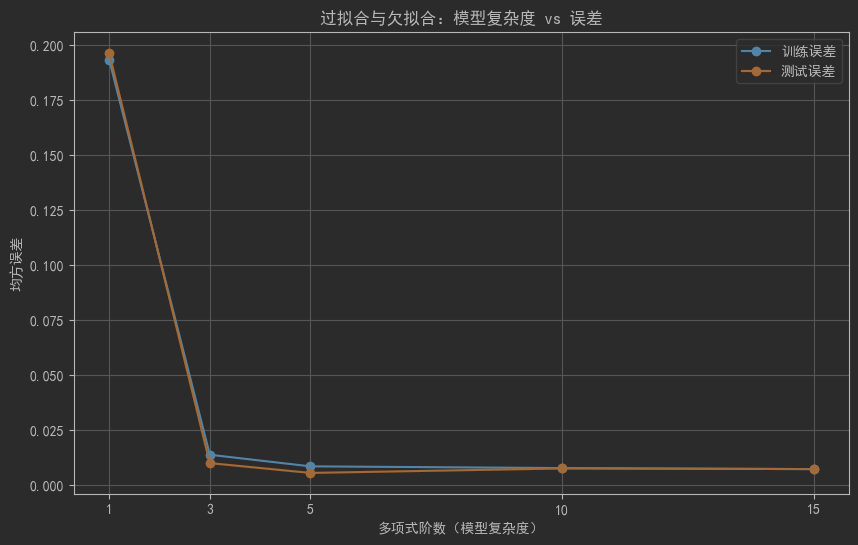

10.5 正則化處理

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split# 生成高維稀疏數據（模擬維度詛咒場景）
X, y = make_regression(n_samples=100, n_features=20, noise=0.1, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 訓練普通線性回歸和L2正則回歸
lr = LinearRegression()
ridge = Ridge(alpha=1.0)  # alpha是正則化強度lr.fit(X_train, y_train)
ridge.fit(X_train, y_train)# 輸出參數對比
print("普通線性回歸參數（絕對值）：", np.abs(lr.coef_).round(4))
print("L2正則回歸參數（絕對值）：   ", np.abs(ridge.coef_).round(4))# 繪制泛化誤差對比
plt.figure(figsize=(8, 5))
plt.bar(['普通線性回歸', 'L2正則回歸'],[np.mean((lr.predict(X_test)-y_test)**2),np.mean((ridge.predict(X_test)-y_test)**2)],color=['skyblue', 'lightcoral'])
plt.ylabel('測試集均方誤差')
plt.title('正則化對泛化能力的影響')
plt.grid(axis='y', linestyle='--')
plt.show()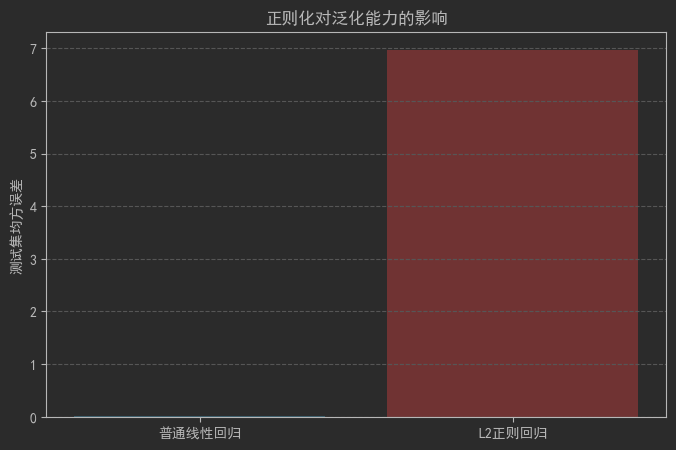

10.6 神經網絡簡單構建

# 導入必要庫
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt# ---------------------- 1. 數據準備 ----------------------
# 定義數據預處理（歸一化 + 轉換為張量）
transform = transforms.Compose([transforms.ToTensor(),  # 將PIL圖像轉為Tensor（形狀：[1,28,28]）transforms.Normalize((0.1307,), (0.3081,))  # MNIST全局均值0.1307，標準差0.3081
])# 加載訓練集和測試集
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)# 創建數據加載器（批量加載數據）
batch_size = 64
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)# ---------------------- 2. 定義神經網絡模型 ----------------------
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()# 定義網絡層結構：輸入層→隱藏層→輸出層self.layers = nn.Sequential(nn.Linear(in_features=28 * 28, out_features=128),  # 輸入層（784→128）nn.ReLU(),  # 激活函數（引入非線性）nn.Linear(in_features=128, out_features=64),   # 隱藏層（128→64）nn.ReLU(),nn.Linear(in_features=64, out_features=10)     # 輸出層（64→10，對應0-9分類）)def forward(self, x):# 前向傳播：展平圖像（從[64,1,28,28]→[64,784]）→通過各層x = x.view(x.size(0), -1)  # 展平操作（關鍵！）x = self.layers(x)return x# ---------------------- 3. 初始化模型、損失函數和優化器 ----------------------
model = SimpleNN()
criterion = nn.CrossEntropyLoss()  # 多分類交叉熵損失（內置Softmax）
optimizer = optim.Adam(model.parameters(), lr=0.001)  # Adam優化器（自適應學習率）# ---------------------- 4. 訓練模型 ----------------------
epochs = 10  # 訓練輪數
train_losses = []  # 記錄每輪訓練損失
train_accuracies = []  # 記錄每輪訓練準確率for epoch in range(epochs):model.train()  # 開啟訓練模式（影響Dropout/BatchNorm等層）running_loss = 0.0correct = 0total = 0for batch_idx, (images, labels) in enumerate(train_loader):# 前向傳播outputs = model(images)loss = criterion(outputs, labels)# 反向傳播 + 優化optimizer.zero_grad()  # 清空梯度loss.backward()        # 計算梯度optimizer.step()       # 更新參數# 統計指標running_loss += loss.item()_, predicted = torch.max(outputs.data, 1)  # 獲取預測類別（概率最大的索引）total += labels.size(0)correct += (predicted == labels).sum().item()# 每100個batch打印一次日志if (batch_idx+1) % 100 == 0:print(f'Epoch [{epoch+1}/{epochs}], Batch [{batch_idx+1}/{len(train_loader)}], 'f'Loss: {running_loss/100:.4f}, Acc: {100*correct/total:.2f}%')running_loss = 0.0# 記錄本輪平均損失和準確率avg_loss = running_loss / len(train_loader)train_losses.append(avg_loss)train_acc = 100 * correct / totaltrain_accuracies.append(train_acc)print(f'Epoch [{epoch+1}/{epochs}] 完成，平均損失: {avg_loss:.4f}, 訓練準確率: {train_acc:.2f}%')# ---------------------- 5. 測試模型 ----------------------
model.eval()  # 開啟評估模式（關閉Dropout/BatchNorm等）
test_correct = 0
test_total = 0with torch.no_grad():  # 關閉梯度計算（節省內存）for images, labels in test_loader:outputs = model(images)_, predicted = torch.max(outputs.data, 1)test_total += labels.size(0)test_correct += (predicted == labels).sum().item()print(f'測試集準確率: {100 * test_correct / test_total:.2f}%')# ---------------------- 6. 可視化訓練過程 ----------------------
plt.figure(figsize=(12, 4))# 損失曲線
plt.subplot(1, 2, 1)
plt.plot(range(1, epochs+1), train_losses, 'bo-', label='訓練損失')
plt.xlabel('輪數')
plt.ylabel('損失')
plt.title('訓練損失變化')
plt.legend()# 準確率曲線
plt.subplot(1, 2, 2)
plt.plot(range(1, epochs+1), train_accuracies, 'ro-', label='訓練準確率')
plt.xlabel('輪數')
plt.ylabel('準確率 (%)')
plt.title('訓練準確率變化')
plt.legend()plt.tight_layout()
plt.show()