? ? ? ? 兩種最小生成樹算法講解

prim算法精講

卡碼網53. 尋寶

????????本題題目內容為最短連接，是最小生成樹的模板題，那么我們來講一講最小生成樹。最小生成樹可以使用prim算法也可以使用kruskal算法計算出來。本篇我們先講解prim算法。

????????最小生成樹是所有節點的最小連通子圖，即：以最小的成本（邊的權值）將圖中所有節點鏈接到一起。圖中有n個節點，那么一定可以用n-1條邊將所有節點連接到一起。

????????prim算法是從節點的角度采用貪心的策略每次尋找距離最小生成樹最近的節點并加入到最小生成樹中。

????????prim算法核心就是三步，我稱為prim三部曲，大家一定要熟悉這三步，代碼相對會好些很多：

1. 第一步，選距離生成樹最近節點
2. 第二步，最近節點加入生成樹
3. 第三步，更新非生成樹節點到生成樹的距離（即更新minDist數組）

????????同時，因為使用一維數組，數組的下標和數組如何賦值很重要，不要搞反，導致結果被覆蓋。

? ? ? ? 一定要理解minDist數組，簡單說就是一棵樹不斷記錄離自己最近的節點，并吸收進來，再不斷循環這個過程

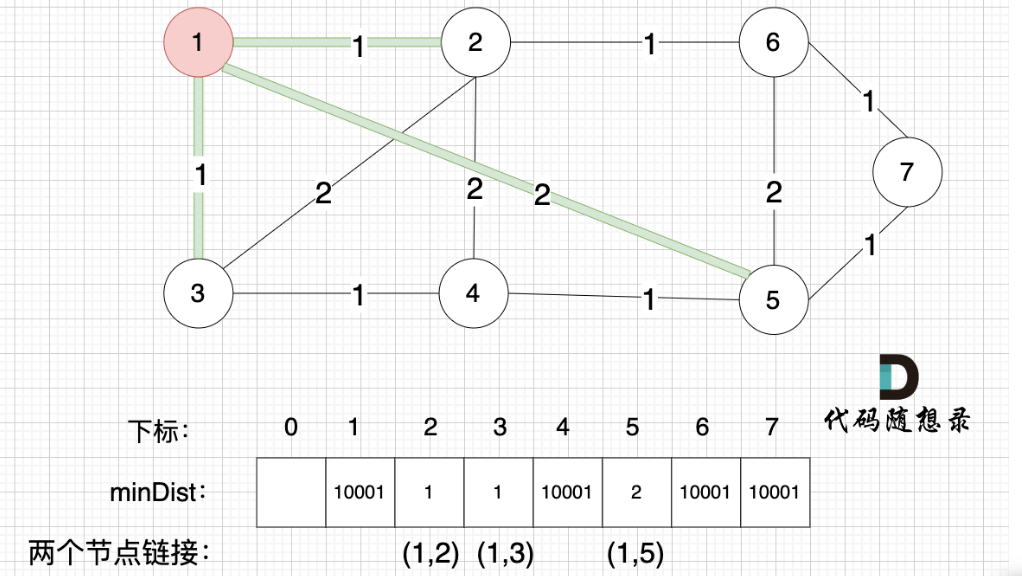
????????不斷吸收新節點，不斷以樹外節點離樹最近的距離做更新，并更新樹，循環，最后達到下圖效果，具體過程為綠色部分不斷延伸（即minDist數組不斷更新），最終計算數組和即可

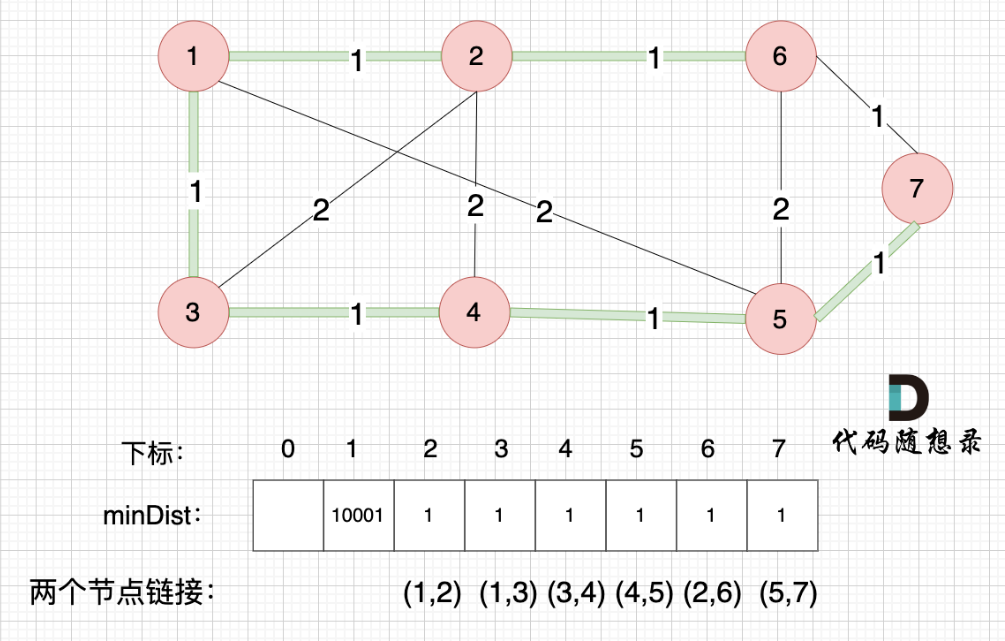
代碼實現

????????記錄邊，注意初始化數組大小

def prim(v, e, edges):"""Prim算法實現，用于求解無向連通圖的最小生成樹(MST)總權重參數:v: 頂點數量e: 邊的數量edges: 邊的列表，每個元素為元組(x, y, k)，表示頂點x與y之間的邊權重為k返回:最小生成樹的總權重"""import sysimport heapq  # 雖然導入了heapq但未使用，可能是預留或之前版本的殘留# 初始化鄰接矩陣，大小為(v+1)x(v+1)（頂點編號從1開始）# 初始值設為10001表示無窮大（假設所有邊的權重都小于此值）grid = [[10001] * (v + 1) for _ in range(v + 1)]# 讀取邊的信息并填充鄰接矩陣# 由于是無向圖，x到y和y到x的權重相同for edge in edges:x, y, k = edge  # x和y為兩個頂點，k為邊的權重grid[x][y] = kgrid[y][x] = k# minDist數組：記錄每個非樹節點到生成樹的最短距離# 索引0未使用（頂點編號從1開始）minDist = [10001] * (v + 1)# 從頂點1開始構建生成樹，因此將其到生成樹的距離設為0minDist[1] = 0# isInTree數組：標記頂點是否已加入生成樹# True表示已加入，False表示未加入isInTree = [False] * (v + 1)# Prim算法主循環：需要加入v-1條邊（構建包含所有v個頂點的樹）for i in range(1, v):# 1. 找到當前未加入生成樹且距離最近的頂點cur = -1  # 存儲當前選中的頂點minVal = sys.maxsize  # 存儲當前最小距離（初始為系統最大整數）# 遍歷所有頂點，尋找符合條件的頂點for j in range(1, v + 1):# 條件：未加入生成樹 且 距離生成樹更近if not isInTree[j] and minDist[j] < minVal:minVal = minDist[j]  # 更新最小距離cur = j  # 更新選中的頂點# 2. 將找到的最近頂點加入生成樹isInTree[cur] = True# 3. 更新所有未加入生成樹的頂點到生成樹的最短距離# 以剛加入的cur頂點為中間點，檢查是否有更短路徑for j in range(1, v + 1):# 條件：未加入生成樹 且 通過cur頂點能獲得更短距離if not isInTree[j] and grid[cur][j] < minDist[j]:minDist[j] = grid[cur][j]  # 更新最短距離# parent[j] = cur; // 記錄最小生成樹的邊 （注意數組指向的順序很重要）# 計算最小生成樹的總權重：累加頂點2到v的最小距離（頂點1為起點，距離0）result = sum(minDist[2:v+1])return resultif __name__ == "__main__":"""程序入口：讀取輸入數據并調用prim函數計算結果"""import sys# 讀取所有輸入數據（一次性讀取提高效率，適用于大數據量）input = sys.stdin.readdata = input().split()  # 將輸入按空白字符分割為列表# 解析頂點數和邊數（前兩個元素）v = int(data[0])e = int(data[1])# 解析所有邊的信息edges = []index = 2  # 從第三個元素開始是邊的信息for _ in range(e):x = int(data[index])y = int(data[index + 1])k = int(data[index + 2])edges.append((x, y, k))  # 將邊信息存入列表index += 3  # 移動到下一條邊的起始位置# 調用prim算法計算結果并輸出result = prim(v, e, edges)print(result)

kruskal算法精講

? ? ? ? 通過貪心的思路，從邊出發，（在是否同一集合的情況下判斷）不斷吸收最小權值的邊。再次注意本題是要求連接所有節點！！

????????但在代碼中，如果將兩個節點加入同一個集合，又如何判斷兩個節點是否在同一個集合呢？我們在并查集開篇的時候就講了，并查集主要就兩個功能：

• 將兩個元素添加到一個集合中
• 判斷兩個元素在不在同一個集合

代碼實現

? ? ? ? 本題圖示是綠色線條的不斷延伸（每次多一條邊），上題為以節點為中心不斷更新最短距離數組

????????lambda?是 Python 中的匿名函數，語法為?lambda 參數: 表達式，通常用于簡化代碼，lambda?中的?edge?是一個形參，sort?方法在遍歷?edges?時會自動將列表中的每個元素作為實參傳給它，因此?edge?能依次指向?edges?中的所有元素

# 定義邊(Edge)類，用于存儲一條邊的信息
class Edge:def __init__(self, l, r, val):self.l = l      # 邊的左頂點self.r = r      # 邊的右頂點self.val = val  # 邊的權重值# 初始化常量和并查集數組
n = 10001               # 最大頂點數限制
father = list(range(n)) # 并查集數組，father[u]表示u的父節點def init():"""初始化并查集，讓每個節點的父節點都是自己"""global fatherfather = list(range(n))def find(u):"""查找節點u的根節點，同時進行路徑壓縮路徑壓縮是為了加快后續的查詢速度"""if u != father[u]:# 遞歸查找根節點，并將當前節點的父節點直接指向根節點father[u] = find(father[u])return father[u]def join(u, v):"""合并兩個集合：將節點v所在的集合合并到節點u所在的集合前提是u和v已經是各自集合的根節點"""u = find(u)v = find(v)if u != v:# 將v的父節點設置為u，實現兩個集合的合并father[v] = udef kruskal(v, edges):"""Kruskal算法實現：求解最小生成樹的總權重參數：v: 頂點數量edges: 邊的列表，每個元素是Edge對象返回：最小生成樹的總權重"""# 1. 按邊的權重從小到大排序（核心步驟）edges.sort(key=lambda edge: edge.val)# 2. 初始化并查集init()# 3. 存儲最小生成樹的總權重result_val = 0# 4. 遍歷所有排序后的邊，嘗試加入生成樹for edge in edges:# 查找兩個頂點所在集合的根節點x = find(edge.l)y = find(edge.r)# 如果根節點不同，說明不在同一個集合，不會形成環if x != y:# 將這條邊加入最小生成樹result_val += edge.val# 合并兩個集合join(x, y)return result_valif __name__ == "__main__":"""程序入口：讀取輸入并調用Kruskal算法計算結果"""import sys# 一次性讀取所有輸入數據input = sys.stdin.readdata = input().split()  # 按空白字符分割成列表# 解析頂點數和邊數v = int(data[0])e = int(data[1])# 解析所有邊的信息edges = []index = 2  # 從第三個元素開始是邊的信息for _ in range(e):v1 = int(data[index])v2 = int(data[index + 1])val = int(data[index + 2])edges.append(Edge(v1, v2, val))  # 創建Edge對象并添加到列表index += 3  # 移動到下一條邊的起始位置# 調用Kruskal算法計算結果并輸出result_val = kruskal(v, edges)print(result_val)

拓展

????????在節點數量固定的情況下，圖中的邊越少，Kruskal 需要遍歷的邊也就越少。而 prim 算法是對節點進行操作的，節點數量越少，prim算法效率就越優。所以在 稀疏圖中，用Kruskal更優。 在稠密圖中，用prim算法更優。

????????為什么邊少的話，使用 Kruskal 更優呢因為 Kruskal 是對邊進行排序的后 進行操作是否加入到最小生成樹。邊如果少，那么遍歷操作的次數就少。

????????Prim 算法 時間復雜度為 O(n^2)，其中 n 為節點數量，它的運行效率和圖中邊樹無關，適用稠密圖。

????????Kruskal算法 時間復雜度 為 nlogn，其中n 為邊的數量，適用稀疏圖