🤔 開篇靈魂拷問
是不是覺得AI知識體系龐大到嚇人?看了一堆快餐視頻還是云里霧里?別慌!這個系列就是要幫你打通任督二脈,用"既快又慢、既深入又膚淺、既有趣又嚴肅"的方式講透AI基礎知識!
💡 核心信念:萬物皆函數
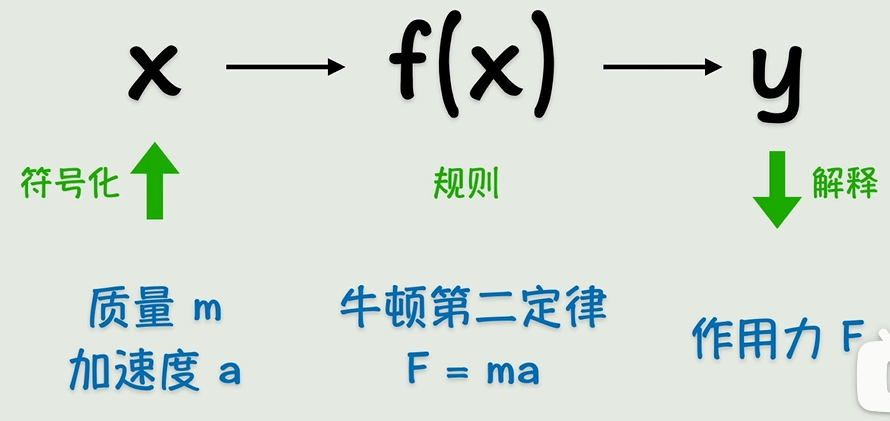
記住!整個AI的出發點就一句話:世界上所有邏輯和知識都能用函數(function)表示。把現實抽象成符號,設置運算規則(函數),算出來結果再反推現實——聽著是不是特有道理?
事實上函數就是一種變換,對數據進行變換得到我們所需要的結果。

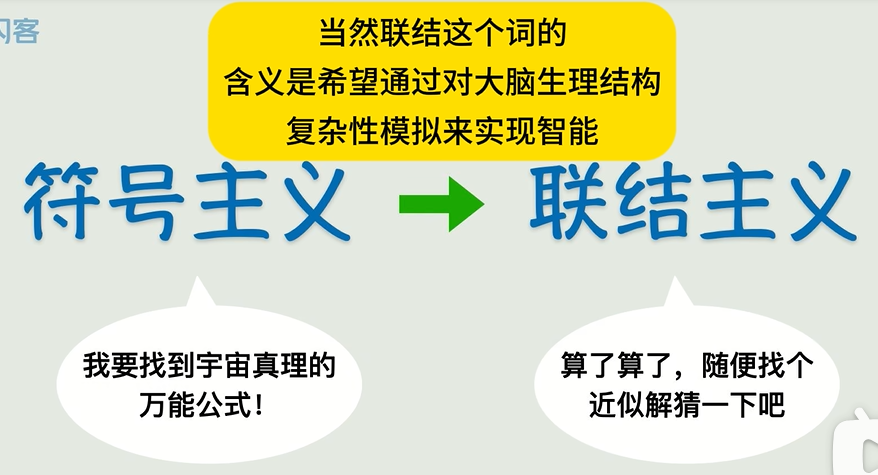
🔍 早期AI的"理想主義":符號主義
早期的人工智能->符號主義,即用精確的函數來表示一切。
直角三角形求斜邊用勾股定理(a2+b2=c2),物體受力用F=ma——這些明確規則的函數玩得轉,但遇到圖片識別貓狗這種人類覺得簡單到爆炸的問題,直接變成史詩級難題!連語法明確的語言翻譯都做不到絲滑,更別說復雜的人類智能了...只能說,早期AI還是太年輕,把世界想得太簡單!
擺爛式創新:聯結主義登場
找不到精確函數咋辦?人類終于承認自己"太菜了",發明了猜+簡化的騷操作!比如給一堆X和Y的數據,先瞎猜個函數(比如Y=X),然后慢慢調參數(W和B)讓它貼近真實數據,就算不能完全吻合,差不多就行!這就是現代AI的核心思路——聯結主義!
但是很多時候,我們沒辦法找到一個精確的函數來描述某個關系,(圖中計算機很難識別)
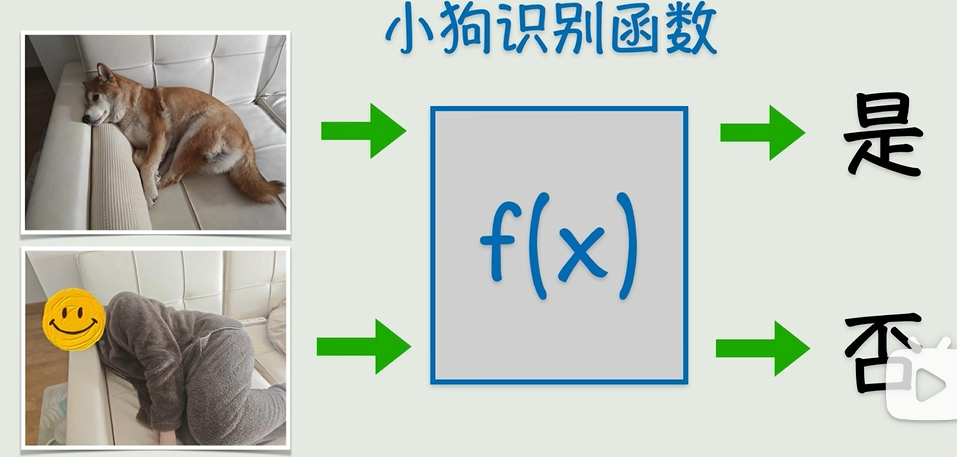
退而求其次選擇一個近似解也不錯,也就是說函數沒必要精確的通過每一個點,它只需要最接近結果就好了,這就是聯結主義。
🚀 連接主義的逆襲
你還別不信!就靠這種"連蒙帶猜"的方法,用很少參數就能實現手寫數字識別,直接打臉當初看不起它的專家!事實證明:結果說話才是硬道理!
雖然“連蒙帶猜”聽起來不靠譜,但實戰效果驚人:用很少的參數就能實現手寫數字識別等任務,證明了有效性后才被重視。

當數據稍微變化一下,出現曲線的時候,簡單的線性函數就沒辦法解決這個問題了。那我們的目標就是將線性函數轉為非線性函數,這可以通過套一個非線性函數來做到,比如平方、正弦函數、指數函數。
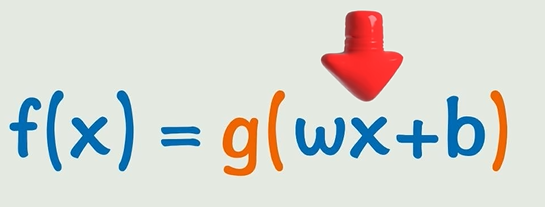
這就是激活函數。激活函數把原來的線性關系轉變成非線性的關系。
激活函數:給直線“掰彎”的魔法 ?
? 線性函數(y=wx+b)太死板,遇到非線性數據就不行。于是給線性變換套個非線性激活函數(如平方、sin、e^x),讓曲線“彎得更靈活”。

🧠 神經網絡進化論
線性函數不夠用?給它套個非線性"馬甲"!比如加個平方、sin函數——這就是激活函數,瞬間讓函數從"死板直線"變身"靈活曲線"!
一層不夠就疊羅漢!線性變換+激活函數反復套娃,中間藏起來的"黑箱子"叫隱藏層,輸入層→隱藏層→輸出層的信號傳播就是前向傳播。理論上,這玩意兒能逼近任意復雜的連續函數!

這還不夠,正常情況下我們不會只有一個輸入,并且只有一個激活函數可能不會達到理想的結果,所以開始嵌套!

像這樣多個輸入,激活函數外面加一次線性變換,再套一個激活函數,并且還可以不斷嵌套。通過這樣的方式,我們可以構造出非常復雜的關系,理論上可以逼近任意的連續函數。
但這樣看起來太復雜了,所以我們引入神經元的概念,
神經網絡:函數套娃的可視化 ?
- 把“線性變換+激活函數”畫成神經元(小圈圈),輸入層→隱藏層→輸出層,每層都是一次函數變換。
- ? 隱藏層:中間層不直接輸出,相當于“套在函數里的函數”,讓模型能表達更復雜關系。
- ? 前向傳播:信號從輸入層到輸出層的計算過程,本質就是分步算一個超復雜函數的值。

圖中的一個小圈就是一個神經元,多個神經元互相連接形成的網狀結構就叫做神經網絡。同時我們可以看到隨著函數式子的嵌套,神經網絡也在拓展,原本的輸出成為了隱藏層:位于輸入層和輸出層之間的中間層。隱藏層的主要作用是對輸入數據進行復雜的特征提取和變換,
核心洞察:神經網絡理論上可以逼近任意連續函數,而整個AI的后續知識,本質上都是為了算出這些神經元之間的w(權重)和b(偏置)!
🎯 終極目標:猜中W和B
不管神經網絡多花里胡哨,本質都是為了猜出所有參數(W權重和B偏置)!從簡單的直線方程到上萬神經元的深度網絡,AI工程師每天都在跟這些參數死磕...至于怎么磕?賣個關子,且聽下回分解!
從神經網絡的圖示來看,就像是一個信號從左向右傳播的過程,這個過程就叫做神經網絡的前向傳播。并且神經網絡的層數和每一層的神經元都可以疊加,這樣就可以構成一個非常復雜的非線性函數。看起來復雜,但是我們的目標還是一開始說的:找到一個近似解,也就是根據已知的x、y猜出所有的w和b。








與調優詳解)







)



的實用指南)