1. 什么是決策樹

學過數據結構與算法的小伙伴應該對樹不陌生吧，這里的決策樹也是大同小異的，只是每次反之都有一個條件來決定流向的。

1.1 決策節點

通過條件判斷而進行分支選擇的節點。如：將某個樣本中的屬性值(特征值)與決策節點上的值進行比較，從而判斷它的流向。

1.2 葉子節點

沒有子節點的節點，表示最終的決策結果。

1.3 決策樹的深度

所有節點的最大層次數。

決策樹具有一定的層次結構，根節點的層次數定為0，從下面開始每一層子節點層次數增加

1.4 決策樹優點：

可視化 - 可解釋能力-對算力要求低

1.5 決策樹缺點：

容易產生過擬合，所以不要把深度調整太大了。

2. 為什么有決策樹這個算法

決策樹的出現，本質上是為了模擬人類的結構化決策過程，并解決實際場景中 “如何從數據中提煉規則” 的問題。具體原因可從以下角度理解：

2.1?模擬人類決策邏輯
人類在做決策時，往往會通過一系列 “是非判斷” 逐步縮小范圍。例如：買水果時，先看 “是否成熟”→ 再看 “價格是否合理”→ 最后決定 “買不買”；醫生診斷時，先問 “是否發燒”→ 再查 “是否咳嗽”→ 最后判斷 “可能的疾病”。決策樹正是將這種 “層層判斷” 的邏輯轉化為數學模型，用樹狀結構（根節點→內部節點→葉節點）清晰呈現決策步驟，讓機器能像人一樣 “有條理地思考”。

2.2 解決 “從數據到規則” 的轉化問題

現實中，很多數據隱含著可解釋的決策規則（比如 “什么樣的用戶會流失”“哪些貸款申請有風險”），但這些規則往往混雜在大量數據中，難以直接觀察。
決策樹通過算法自動從數據中挖掘這些規則（例如 “如果用戶月消費＞500 元且使用時長＞2 年，則流失概率低”），并以樹狀圖的形式可視化，讓規則變得可理解、可復用。

2.3 應對復雜場景的靈活性
與早期的簡單模型（如線性回歸）相比，決策樹能處理非線性關系（例如 “年齡對購買意愿的影響不是簡單的正比或反比”），也能同時處理數值型數據（如收入）和類別型數據（如性別），適用場景更廣泛。

舉個例子

我們的決策樹深度越深是不是就分的越詳細，然后就越正確，但是這樣往往就會過度擬合了，我們前面介紹到決策樹算力較低那這個地方體現在哪里，看上面的例子，左邊和右邊的起始條件不同，所以分類的過程也是不一樣的，但是我的起始條件對分類越重要是不是就能越快得出結果，那我們怎么來確定這個特征的重要程度呢？

3. 基于信息增益決策樹的建立

3.1 信息熵

熵這個詞出現在熱力學中，熵越大，說明事物越混亂，越不確定，在機器學習中，特征越是不確定是不是就越難確定最終的分類結果，這種不確定性在這里成為信息熵，熵的大小取決于 “不同取值的概率分布是否均勻”，比如

用 “身高” 預測 “是否喜歡吃辣”。假設身高 160cm 的人中，50% 喜歡吃辣、50% 不喜歡；身高 170cm 的人中，同樣是 50% 喜歡、50% 不喜歡…… 無論身高取什么值，目標類別的分布都接近均勻。此時 “身高” 的不確定性高（熵大），但身高數據本身是準確測量的（比如用卷尺精確記錄），只是它和 “是否喜歡吃辣” 無關。

3.2 信息商的公式

3.3 信息增益

信息增益是一個統計量，用來描述一個屬性區分數據樣本的能力。信息增益越大，那么決策樹就會越簡潔。這里信息增益的程度用信息熵的變化程度來衡量, 上面的例子就有信息增益的影子，信息增益公式：

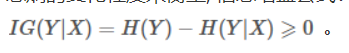
信息增益越大的是不是越能反映和類別的關聯程度，所以越大的特征就放到前面的決策點出。

3.4?信息增益決策樹建立步驟

我們先來算一下信息增益，

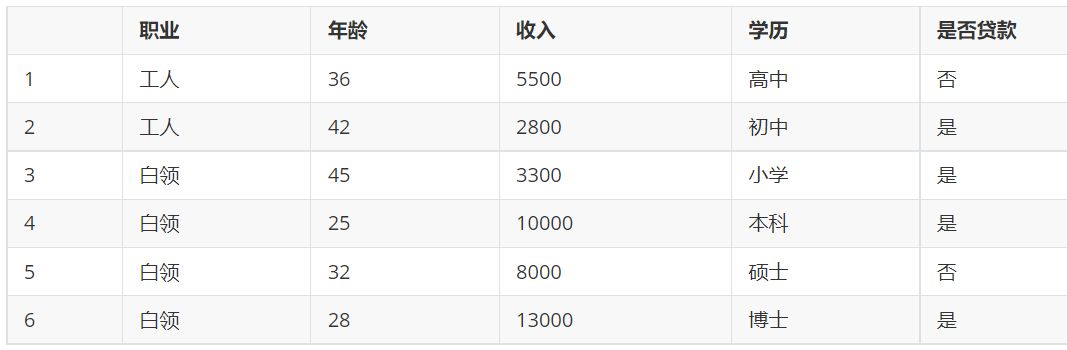
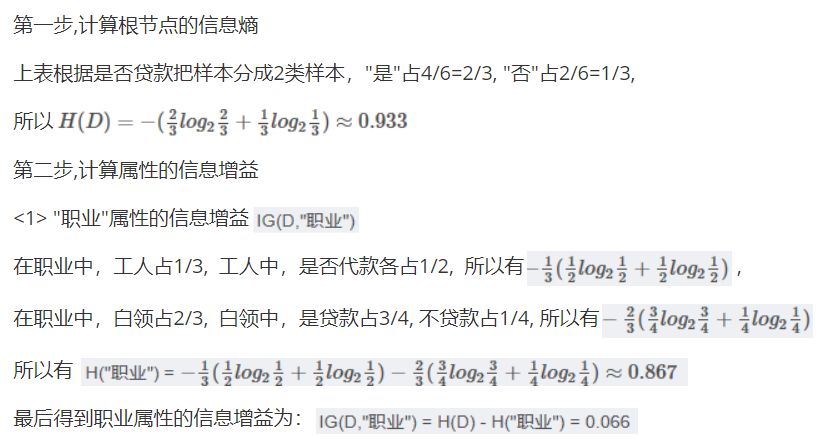
但是這里我們算的是職業他的類別很少，我們可以有具體得分類，要是我們看年齡的信息增益且不是要分好多次，所以我們這里以35為界限，弄一個范圍，假如我們每一個值都歸為一類雖然算力大，但是確實很準的，我們可不能要很準的結果。

假如就是職業算的信息增益最大，那我們就把他放到第一個判斷的決策點，然后我們將這個特征篩選出，對剩下的重新計算，算出新的最大的信息增益。

4 基于基尼指數決策樹的建立(了解)

基尼指數（Gini Index）是決策樹算法中用于評估數據集純度的一種度量，基尼指數衡量的是數據集的不純度，或者說分類的不確定性。在構建決策樹時，基尼指數被用來決定如何對數據集進行最優劃分，以減少不純度。

基尼指數的計算

對于一個二分類問題，如果一個節點包含的樣本屬于正類的概率是 (p)，則屬于負類的概率是 (1-p)。那么，這個節點的基尼指數 (Gini(p)) 定義為：

基尼指數的意義

• 當一個節點的所有樣本都屬于同一類別時，基尼指數為 0，表示純度最高。

• 當一個節點的樣本均勻分布在所有類別時，基尼指數最大，表示純度最低。

基尼指數越小的，越排到前面，確定了第一個之后，后面的也繼續重復操作。

5 api

class sklearn.tree.DecisionTreeClassifier(....)
參數：
criterion "gini" "entropy” 默認為="gini"?
當criterion取值為"gini"時采用 基尼不純度（Gini impurity）算法構造決策樹，
當criterion取值為"entropy”時采用信息增益（ information gain）算法構造決策樹.
max_depth?? ?int, 默認為=None ?樹的最大深度

# 可視化決策樹
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
參數：
estimator決策樹預估器
out_file生成的文檔
feature_names節點特征屬性名
功能:
把生成的文檔打開，復制出內容粘貼到"http://webgraphviz.com/"中，點擊"generate Graph"會生成一個樹型的決策樹圖

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier, export_graphviz# 1）獲取數據集
iris = load_iris()# 2）劃分數據集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)#3）標準化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)# 4）決策樹預估器
estimator = DecisionTreeClassifier(criterion="entropy")estimator.fit(x_train, y_train)# 5）模型評估，計算準確率
score = estimator.score(x_test, y_test)
print("準確率為：\n", score)# 6）預測
index=estimator.predict([[2,2,3,1]])
print("預測:\n",index,iris.target_names,iris.target_names[index])# 可視化決策樹
export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)