目錄

📁?JZ53?數字在升序數組中出現的次數?編輯

📁?JZ4?二維數組中的查找?編輯

📁?JZ11?旋轉數組的最小數字

📁?JZ38?字符串的排列?編輯

---

📁?JZ53?數字在升序數組中出現的次數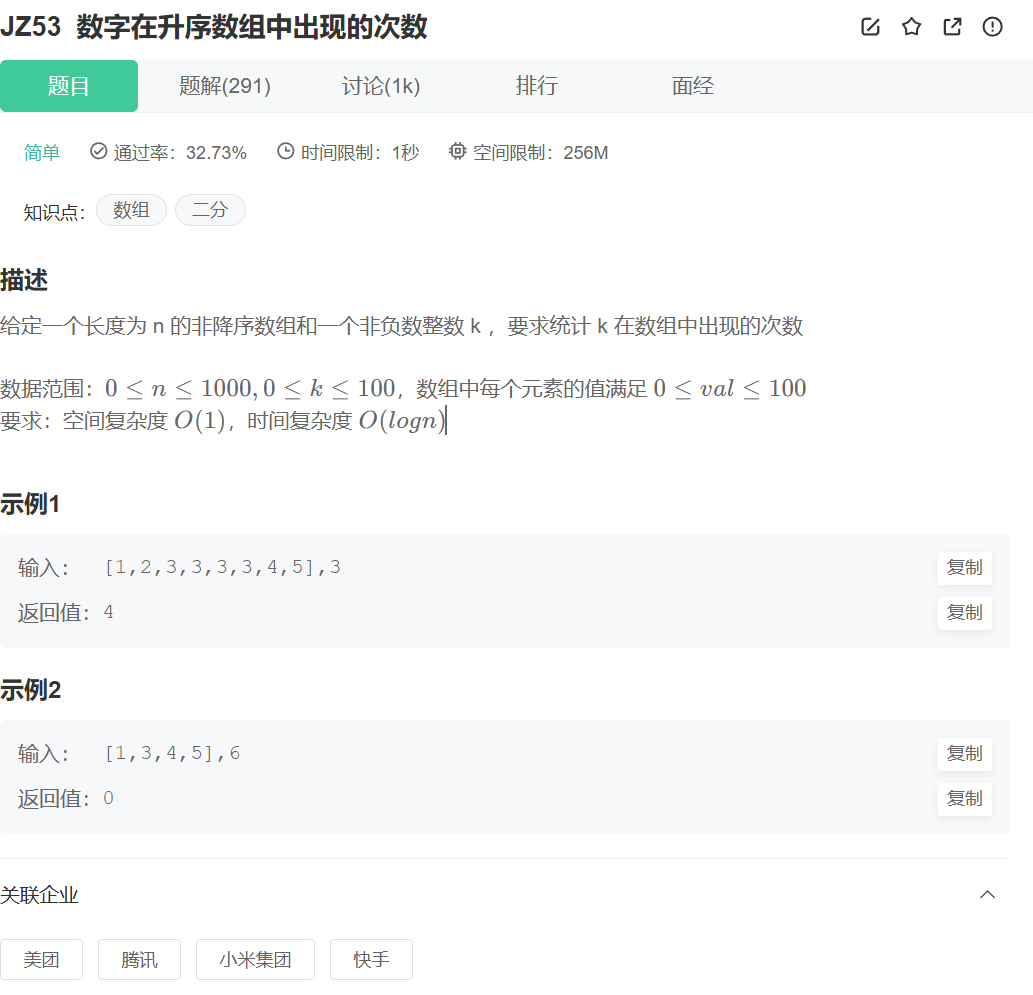

? ? ? ? 這就是一道簡單的模板題，使用二分查找的模板往上套即可。如果對二分還不是很熟悉的，可以看一下我寫的這一篇文章，講解的還是比較基礎簡單的：【算法雜貨鋪】二分算法_二分樸素-CSDN博客

#include <limits>
class Solution {
public:int GetNumberOfK(vector<int>& nums, int k) {if(nums.size() == 0)return 0;int left = 0, right = nums.size() - 1;int begin = -1 , end = -1;while(left < right){int mid = (left + right) >> 1;if(nums[mid] < k)left = mid + 1;elseright = mid;}if(nums[left] == k)begin = left;if(begin == -1)return 0;left = 0, right = nums.size() - 1;while(left < right){int mid = (left + right + 1) >> 1;if(nums[mid] > k)right = mid - 1;elseleft = mid;}if(nums[left] == k)end = left;return end - begin + 1;}
};

📁?JZ4?二維數組中的查找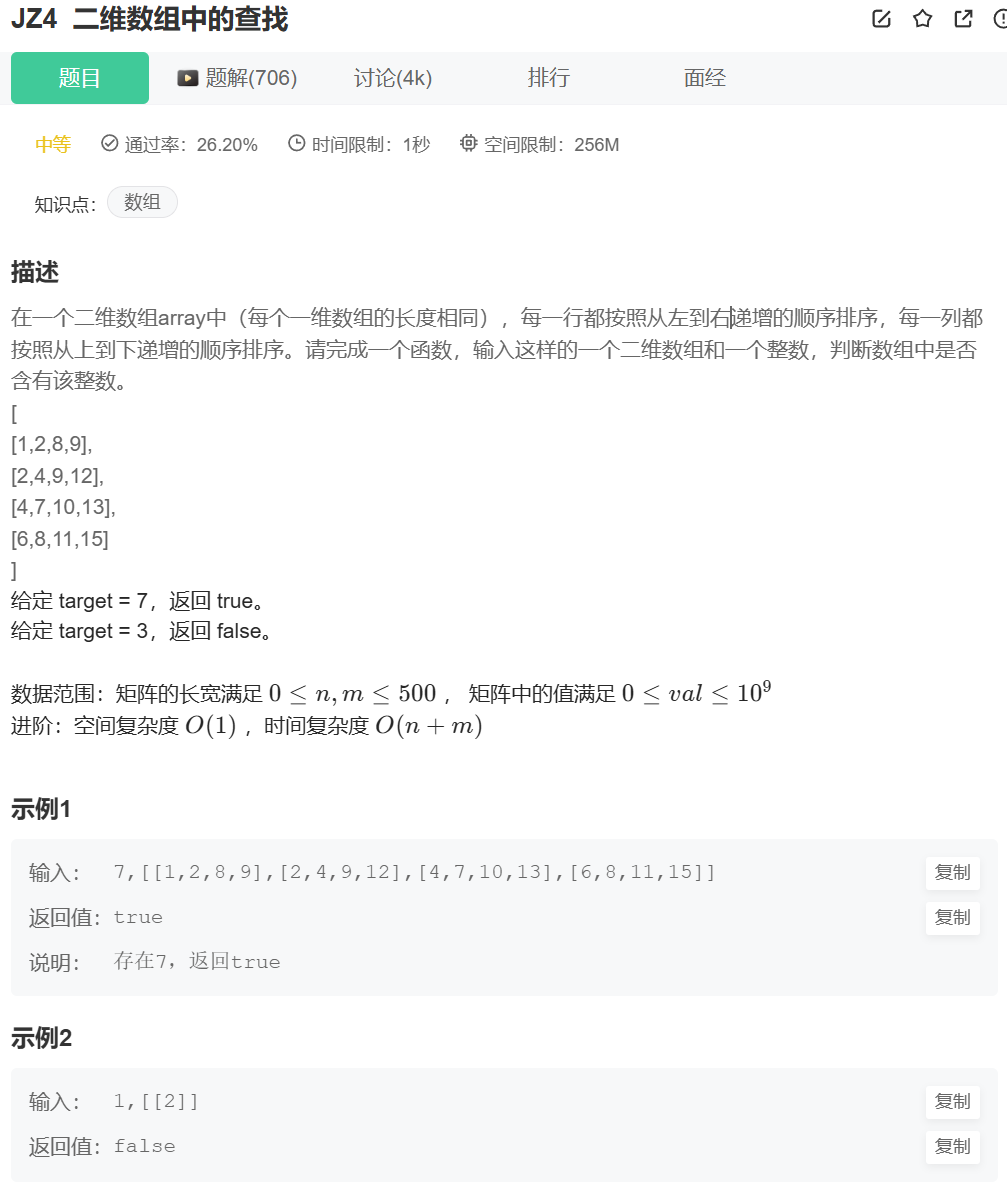

? ? ? ? 根據這個二維數組的性質，搜索目標數。

????????"每一行都按照從左到右遞增的順序排序，每一列都按照從上到下遞增的順序排序。"

? ? ? ? 我們從左上角開始，面臨如下幾種情況：

1. target == 當前位置：直接返回true.

2.?target >?當前位置：說明比當前行中的所有元素都要大，直接去下一行查找.

3.?target <?當前位置：說明當前行可能存在目標元素，去前面的位置查找。因為列是從小到大向下遞增的，如果當前行沒有，要去下一行查找（?target >?當前位置），在下一行中可以直接從當前行的列位置開始。

? ? ? ? 行和列必須在指定范圍內。

class Solution {
public:bool Find(int target, vector<vector<int> >& array) {int m = array.size(), n = array[0].size();if(m == 0 || n == 0)return false;int row = 0, col = n - 1;while(row < m && col >= 0){if(array[row][col] == target)return true;else if(array[row][col] > target)col--;else++row;}return false;}
};

📁?JZ11?旋轉數組的最小數字

? ? ? ? 旋轉數組后，無非就下面這幾種情況：

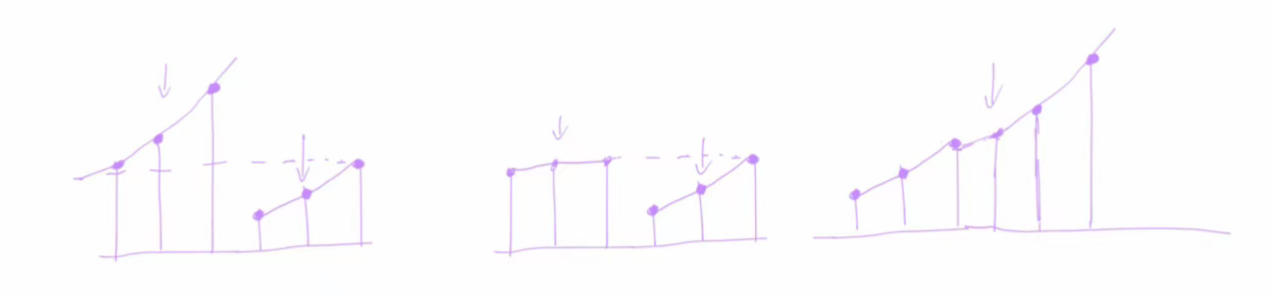
? ? ? ? 將一個有序的數組分成一個或兩個有序的數組。

1. mid > right：說明最小節點一定在mid的右側.

2. mid == right: 不確定，逐漸縮小右邊界范圍.

3. mid < right: 最小節點一定在mid的左側.

class Solution {
public:int minNumberInRotateArray(vector<int>& nums) {int l = 0, r = nums.size() - 1;while(l < r){int mid = (l + r) >> 1;if(nums[mid] > nums[r])l = mid + 1;else if(nums[mid] == nums[r])--r;elser = mid;}return nums[l];}
};

📁?JZ38?字符串的排列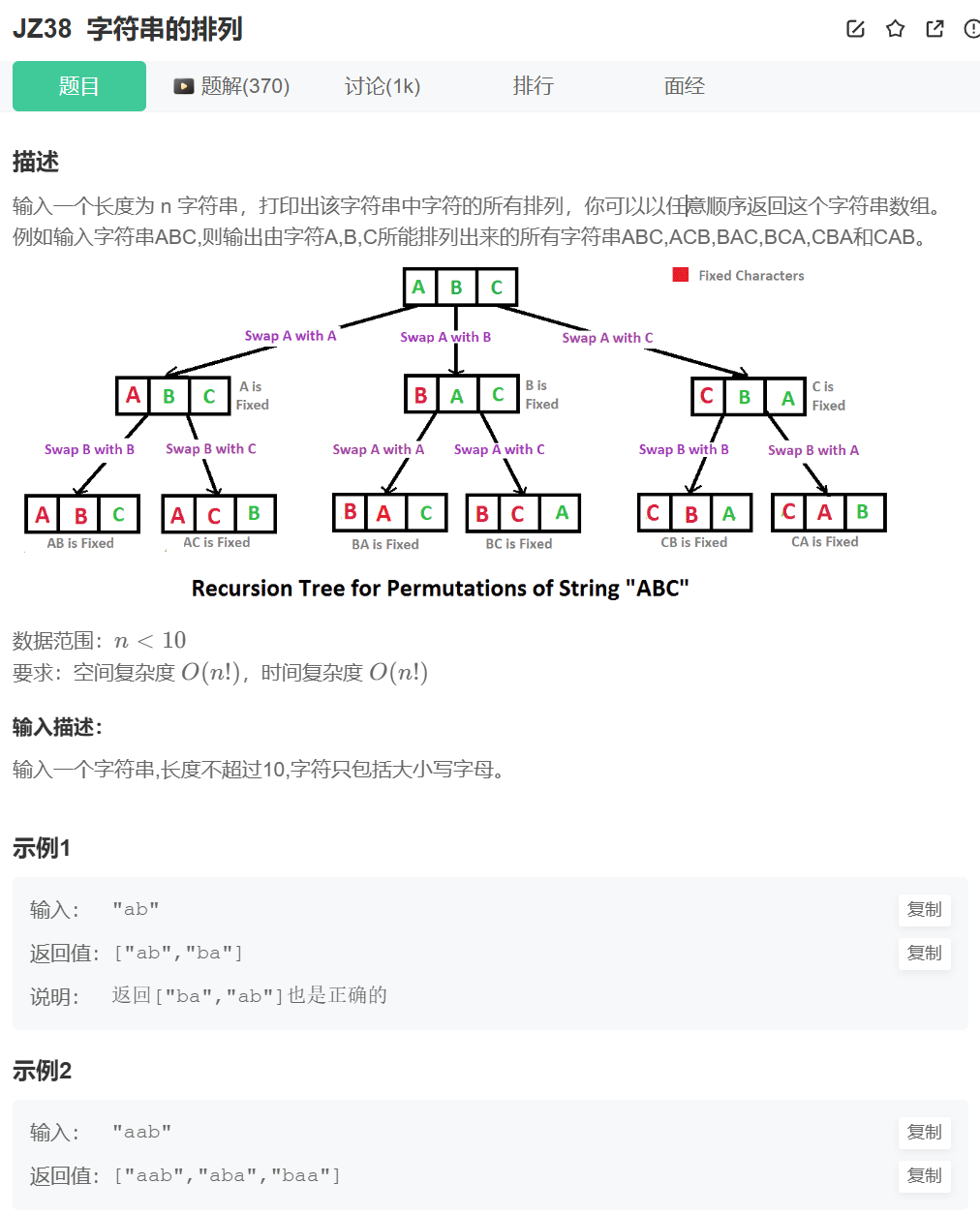

? ? ? ? 思路就是：將一個字符串str，生成其所有可能的排列（全排列），并返回去重后的結果。

#include <unordered_map>
#include <vector>
class Solution {
public:vector<string> ret;string path;unordered_set<string> s;vector<string> Permutation(string str) {int n = str.size();vector<bool> arr(n + 1 , false);dfs(str, arr);return ret;}void dfs(string str, vector<bool>& arr){if(path.size() == str.size() && s.find(path) == s.end()){ret.push_back(path);s.insert(path);return ;}for(int i = 0 ; i < str.size(); ++i){if(arr[i] == false){arr[i] = true;path += str[i];dfs(str, arr);arr[i] = false;path.pop_back();}}}
};