A semi-empirical approach to simulating the Dst index in global MHD models of Earth’s magnetosphere

1? Introduction
Dst指數?(Disturbance storm time index, 地磁暴時擾動指數) 是描述磁暴活動強度應用最廣泛的指數,對于研究地磁擾動和磁暴具有重要意義。Dst指數的基本概念最初由Sugiura (1960)提出。它通過對四個低緯度觀測臺站測量的地磁場水平分量減去平靜期的平均變化量而獲得。選擇這些觀測臺是為了最小化極光區電流 (auroral currents)?和赤道電急流 (equatorial electric currents)?的影響,并且它們的經度在全球范圍內大致均勻分布。然而,Dst指數的時間分辨率僅為1小時,這對于描述某些地磁事件來說顯得相對較長。作為一種替代方案,SYM-H指數 (Symmetric disturbance field index in H-component, H分量對稱擾動場指數)?可被視為升級版的Dst指數,具有一分鐘的分辨率,對于中度和強烈磁暴,其偏差通常小于20 nT。與Dst指數不同,SYM-H指數使用來自全球赤道區域經度均勻分布的六個低緯度和中緯度地面磁力儀臺站的數據進行計算。
從物理意義上講,Dst指數的大小是衡量赤道環電流 (equatorial ring current)?強度的尺度,通常可以反映磁暴的強度。Burton等人 (1975) 根據Dst指數的最小值將磁暴分為四個級別:最小值為?30至?50 nT的為小磁暴 (minor storms),?50至?100 nT的為中等磁暴 (moderate storms),?100至?200 nT的為強烈磁暴 (intense storms),以及最小值超過?200 nT的為超級磁暴 (super storms)。
準確預測Dst指數對于磁暴及相關空間天氣預報研究具有重要價值。人們已經開發了多種利用觀測到的太陽風參數作為輸入來預測Dst指數的方法。通常,它們可以分為三類,包括經驗公式 (empirical formula)、機器學習方法 (machine-learning methods)?和基于物理的模型 (physics-based models)。其中,經驗公式模型因其在數值實現上相對簡單而被最廣泛使用。在早期研究中,Burton等人 (1975) 提出了一個計算Dst指數的經驗公式,該公式使用與太陽風參數相關的項作為微分方程中的系數,考慮了粒子從等離子體片 (plasma sheet)?注入內磁層 (inner magnetosphere)?的過程,并強調了行星際磁場 (Interplanetary Magnetic Field, IMF)?南向分量在計算中的關鍵作用。隨后,該經驗模型的一些擴展版本被推導出來并應用于相關領域,并且自Burton等人 (1975) 以來,已有許多基于此經驗公式的研究 。
機器學習和神經網絡技術已廣泛應用于Dst指數的建模和預測?(Lu JY et al., 2016; Camporeale, 2019; Xu WW et al., 2023)。早在20世紀90年代,就有多次嘗試利用神經網絡預測Dst指數。Jankovi?ová等人 (2002) 采用全連接神經網絡預測Dst指數,開發了一個能夠利用ACE衛星數據提前兩小時預測該指數的模型。Lundstedt等人 (2002) 研究了太陽風動壓 (dynamic pressure)?變化和環電流注入的響應特性及衰減,發現當行星際磁場轉向南向時,環電流注入速率與太陽風動壓成正比。他們將這一發現應用于Dst指數的預測,提高了預測精度。Caswell (2014) 利用IMF分量、太陽風質子密度、等離子體速度和等離子體流壓來提前一小時預測Dst指數。Lazzús等人 (2017) 引入了一個人工神經網絡 (Artificial Neural Network, ANN)?模型,在1至6小時的提前時間內實現了更高精度的Dst指數預測。基于ANN模型的類似工作也已被開展,以期獲得更好的預測精度和穩定性 (Lethy et al., 2018; Xu SB et al., 2020; Park et al., 2021)。
基于物理的模型通常通過求解描述環電流動力學的第一性原理方程來預測誘導產生的Dst指數。一些模型采用Dessler?Parker?Sckopke方程,將模擬環電流內的總能量轉化為Dst,然后計算預期的Dst指數,其中還根據太陽風施加的動壓納入了磁層頂電流 (magnetopause currents)?的校正。Rice對流模型 (Rice Convection Model, RCM)?有效地描述了內磁層等離子體的電動力學 。它采用Hilmer和Voigt的磁場描述,結合Siscoe-Hill? 或Weimer?電場模型。該模型基于磁層等離子體的壓力梯度,使用Vasyliunas方程計算場向電流 (field-aligned current)。該電流進而確定電離層電位和電場,然后將其映射回內磁層以完成計算循環。這個過程使得計算環電流的能量成為可能。其他用于模擬環電流動力學的內磁層模型包括RAM-SCB?(Radiation Belt Environment - Scattered Particle model with Self-Consistent magnetic field)、CRCM?(Comprehensive Ring Current Model) 和WINDMI?(Wave and Instability, Nonlinear, Driven, Magnetospheric-Ionospheric model) 模型。RAM-SCB是一個開源模擬代碼,可模擬主要離子種類和電子在方位角、徑向距離、能量、投擲角以及Dst指數等多個參數上的演化。另一方面,CRCM模型能夠準確預測日冕物質拋射 (Coronal Mass Ejection, CME)?驅動的磁暴的Dst指數,但它低估了共轉相互作用區 (Co-rotating Interaction Region, CIR)?驅動的磁暴的該指數,這種差異可能導致對總環電流能量高達一半的潛在高估,原因在于模擬靜態磁場的局限性。最后,WINDMI是一個低階、非線性環電流模型,能夠生成地磁西向極光電集流 (geomagnetic westward auroral electrojet, AL)?指數和Dst指數的輸出。
地球磁層的全球磁流體力學 (Magneto-HydroDynamic, MHD)?模型可以通過結合磁層中不同位置處的電流密度,利用畢奧-薩伐爾定律 (Biot?Savart formula)?計算地球中心的磁場擾動來模擬Dst指數。然而,這些模型無法有效模擬環電流,因為它們無法捕捉內磁層中帶電粒子的漂移運動。因此,必須將內磁層模型集成到全球MHD模型中,才能更準確地模擬Dst指數。此類全球MHD模型的例子包括BATSRUS?(Block Adaptive Tree Solarwind Roe-type Upwind Scheme)、OpenGGCM?(Open Geospace General Circulation Model) 和LFM?。例如,BATSRUS模型有與RCM (De Zeeuw et al., 2004) 和CRCM 耦合的版本。當與內磁層模型集成時,BATSRUS顯著提高了其在磁暴期間復現Dst值的能力,因為如果沒有這個組件,它無法達到低于?30 nT的Dst值 。歐洲日球層預報信息資產 (European Heliospheric Forecasting Information Asset)?與OpenGGCM耦合時,展示了對地磁擾動指數的有效預測,從而增強了空間天氣預報能力 。Rast?tter等人 (2013) 對這些統計和基于物理的模型在計算Dst指數方面的性能進行了全面的回顧和分析。
不同于引入內磁層模型,本文嘗試將經驗公式集成到地球磁層的全球MHD模型中,以模擬Dst指數。本文結構如下:第2節介紹了計算Dst指數的方法,包括全球MHD模型和經驗公式。第3節概述了分析中使用的具體事件和數據集。第4節展示了模擬結果,隨后是對這些事件的討論。最后,第5節總結了結論。
2. 方法 (Methodology)
2.1 全球MHD模型中的Dst指數 (Dst Index in a Global MHD Model)
Dst指數量化了低緯度地面普遍地磁活動的強度,并用于估計地球附近環電流的能量密度。?然而,其他磁層電流系統,如日側磁層頂電流 (dayside magnetopause currents) 和夜側磁尾電流 (nightside tail currents) 也會引起地面磁場擾動,它們可能對Dst指數有次要貢獻。
本工作應用了PPMLR-MHD模型 (PPMLR-MHD model)?的修訂版本。在該模型中,使用了一種為分解本征磁場而設計的HLL型黎曼求解器 (HLL-type Riemann solver)?的擴展,在MUSCL數值格式 (MUSCL numerical scheme)?中更新網格單元界面處的數值通量。在模擬過程中,任何給定網格點處的磁場B通過時變MHD方程在每個時間步長進行數值更新。磁層電流系統是通過持續的上游太陽風擠壓引起的地磁場畸變直接計算得出的。然后,通過歸一化關系?j=?×B?獲得電流密度?j,其中包含了大規模的磁層頂電流 (magnetopause currents)、場向電流 (field-aligned currents)?和磁尾電流 (tail currents)。然而,環電流 (ring currents)?并未產生,因為帶電粒子的梯度和曲率漂移運動無法在單流體MHD近似中再現。
對于Dst指數,這里不考慮四個主要地磁觀測臺的確切位置;而是使用地球中心的磁場擾動來表示地面赤道面上的平均地磁擾動,并將對應的地磁擾動的南北軸向分量定義為Dst指數,遵循先前研究者在全球MHD模擬中采用的類似方法。使用畢奧-薩伐爾定律 (Biot-Savart’s Law),估計的Dst指數表示為地心太陽磁層坐標系 (Geocentric Solar Magnetospheric coordinate system, GSM)?中心處磁場擾動的 z 分量:
![]()
其中 R?是電流密度 j 的空間位置,ΔV?是網格體積。來自所有個體的擾動貢獻在所有網格體積上求和,并累積為Dst指數Dst_{MHD}。該指數的時間分辨率由電流密度?j?決定,而?j?取決于模擬數據輸出的任意間隔。
?在本工作中,選擇一分鐘的分辨率,這與SYM-H指數相同,但遠小于標準Dst指數的一小時分辨率。為簡便起見,在下文中將繼續使用術語 “Dst指數” 來表示模擬的一分鐘分辨率Dst指數。
2.2 來自環電流的經驗Dst指數 (Empirical Dst Index from Ring Current)
全球MHD模型中缺乏環電流模型將導致Dst指數估計結果不一致。?例如,磁暴期間Dst指數的突然下降無法在模擬中復現,這主要依賴于內磁層 (inner magnetosphere) 環電流的增強。Rae等人 (2010) 證明,在全球模擬中,當行星際磁場 (IMF) 南向期間,內磁層物理在塑造開放與閉合磁力線邊界方面起著關鍵作用。
為了克服這一差異,需要將一個基于物理的、嵌入了環電流的內磁層模型集成到現有的全球磁層MHD模型中 (De Zeeuw, 2004)。這里我們嘗試一種不同的方法——使用一個經驗模型 (empirical model)。
Burton等人 (1975) 提出了一種僅從太陽風速度、密度和IMF (行星際磁場) 條件知識計算Dst指數的算法。他們的Dst指數方程(方程中為?Dst*)表示為:
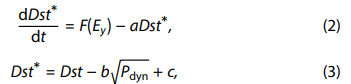
其中:
-
a = 3.6 × 10?? s?1,是與環電流粒子衰減時間相關的系數; -
P_dyn?代表太陽風的動壓 (dynamic pressure); -
b = 0.2 nT/(eV/cm3)1?2?和?c = 20 nT?是系數,分別衡量Dst對太陽風動壓和寧靜期環電流的響應。 -
F(E_y)?代表環電流注入率,它是一個經過延遲和濾波的太陽風電場?E_y?的函數,設定為: -
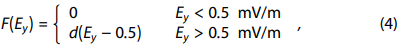
其中?d = -1.5 × 10?3 (nT·m)/(mV·s)?是一個常數,用于衡量注入率對?E_y?的響應程度,假設這種響應是線性的。
-
F(E_y)?的物理意義是代表粒子注入環電流的速率,它是環電流被晨昏方向太陽風電場增強的速率的函數。
在全球MHD模型中,太陽風電場的y分量?E_y?直接從未受擾動的太陽風速度?v?和?GSM坐標系?中?x = 0?平面處的磁場?B?計算得出:
![]()
一旦獲得?E_y?和相應的注入率?F,方程 (2) 和 (3) 便被離散化,以在時間上獲得經驗Dst指數(方程中為?Dst_E):
![]()
注意:?全球磁層電流密度對Dst指數的影響已在全球MHD模型中模擬,可能只考慮來自環電流的貢獻,因此通過設定?b = 0?來忽略太陽風動壓分量。最終,得到以下方程:
![]()
通過這種方式,依賴環電流的Dst指數已通過上述數值實現計算出來,并添加到來自MHD模型的Dst指數中作為最終結果:
![]()
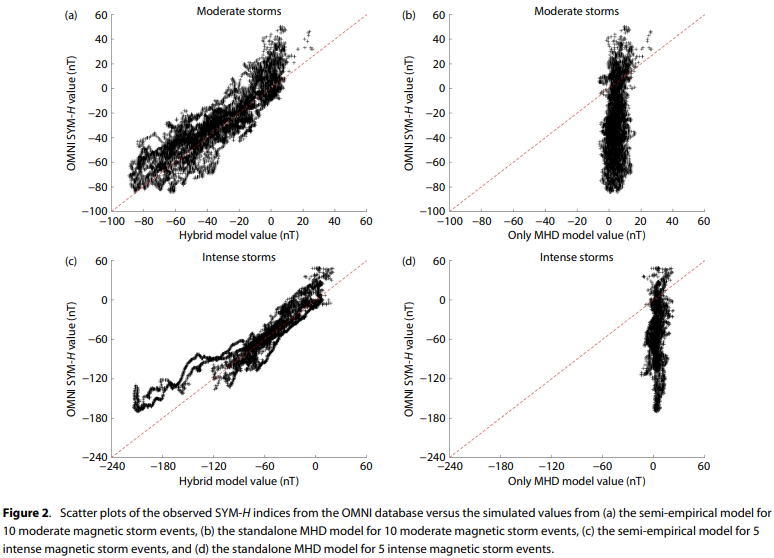
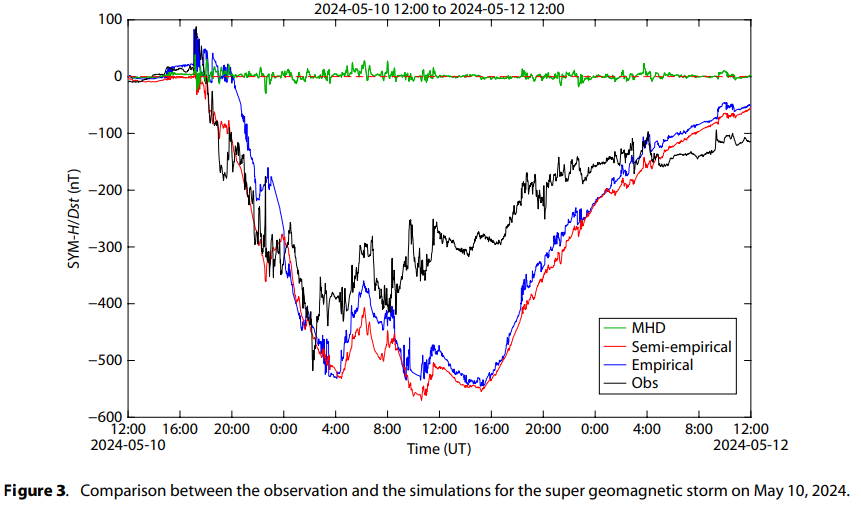
注意:經驗分量?Dst_E?不會產生正值,也不能準確預測地磁暴爆發期間Dst指數的突然開始 (sudden commencement)。?然而,MHD分量?Dst_{MHD}?可以有效地模擬由太陽風動壓變化引起的Dst變化。?因此,這種半經驗模型 (semi-empirical model)?結合了來自基于MHD的磁層電流的Dst貢獻和來自經驗環電流的Dst貢獻,有望在地磁暴期間增強整體模擬性能。模型與觀測相比的詳細性能將在后續內容中展示。
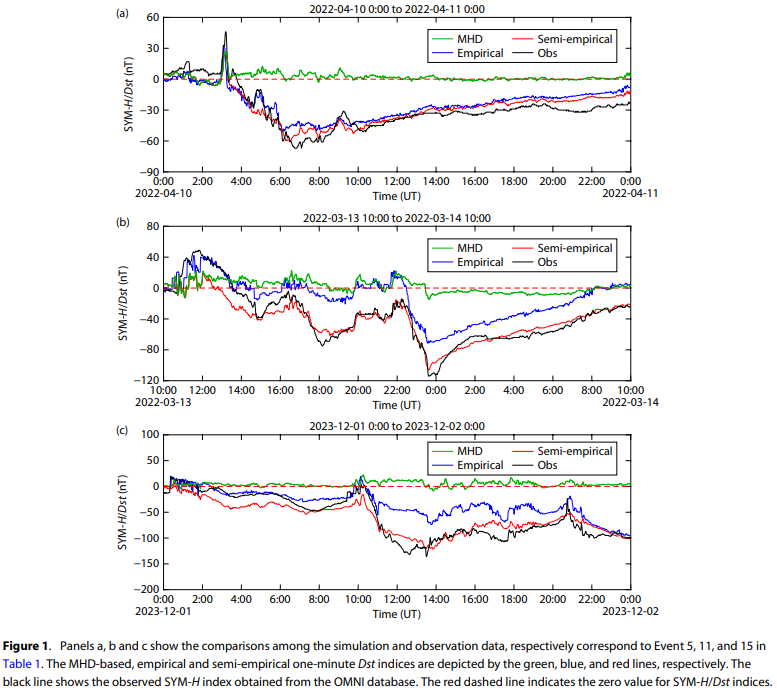
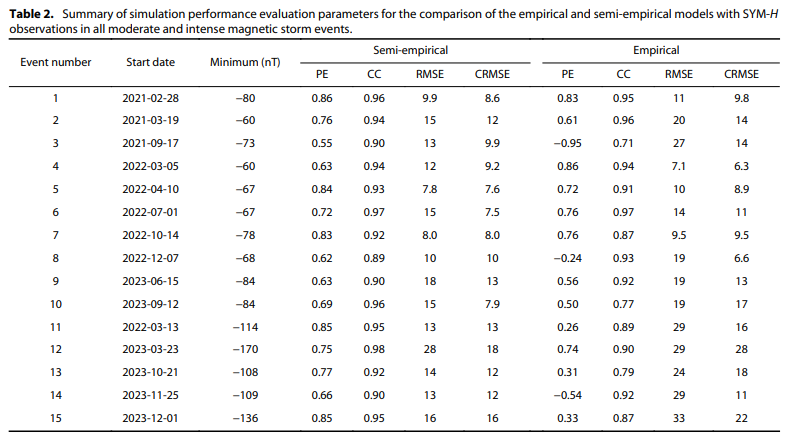





)
漏洞利用工具,支持各版本TP漏洞檢測,命令執行,Getshell)
(git分支保護)(通過設置規則和權限來限制對特定分支的操作的功能))




)
)



)

