深度學習基礎

第一章、參數初始化

我們在構建網絡之后，網絡中的參數是需要初始化的。我們需要初始化的參數主要有權重和偏置，偏重一般初始化為 0 即可，而對權重的初始化則會更加重要，我們介紹在 PyTorch 中為神經網絡進行初始化的方法。

1.1 常見初始化方法

均勻分布初始化, 權重參數初始化從區間均勻隨機取值。即在(-1/√d,1/√d)均勻分布中生成當前神經元的權重，其中d為每個神經元的輸入數量。

正態分布初始化, 隨機初始化從均值為0，標準差是1的高斯分布中取樣，使用一些很小的值對參數W進行初始化。

全0初始化，將神經網絡中的所有權重參數初始化為 0。
全1初始化，將神經網絡中的所有權重參數初始化為 1。
固定值初始化，將神經網絡中的所有權重參數初始化為某個固定值。
kaiming 初始化，也叫做 HE 初始化。 HE 初始化分為正態分布的 HE 初始化、均勻分布的 HE 初始化。
xavier 初始化，也叫做Glorot初始化，該方法的基本思想是各層的激活值和梯度的方差在傳播過程中保持一致。它有兩種，一種是正態分布的 xavier 初始化、一種是均勻分布的 xavier 初始化。

接下來，我們使用 PyTorch 調用相關 API:

import torch
import torch.nn.functional as F
import torch.nn as nn# 1. 均勻分布隨機初始化
def test01():linear = nn.Linear(5, 3)# 從0-1均勻分布產生參數nn.init.uniform_(linear.weight)print(linear.weight.data)# 2. 固定初始化
def test02():linear = nn.Linear(5, 3)nn.init.constant_(linear.weight, 5)print(linear.weight.data)# 3. 全0初始化
def test03():linear = nn.Linear(5, 3)nn.init.zeros_(linear.weight)print(linear.weight.data)# 4. 全1初始化
def test04():linear = nn.Linear(5, 3)nn.init.ones_(linear.weight)print(linear.weight.data)# 5. 正態分布隨機初始化
def test05():linear = nn.Linear(5, 3)nn.init.normal_(linear.weight, mean=0, std=1)print(linear.weight.data)# 6. kaiming 初始化
def test06():# kaiming 正態分布初始化linear = nn.Linear(5, 3)nn.init.kaiming_normal_(linear.weight)print(linear.weight.data)# kaiming 均勻分布初始化linear = nn.Linear(5, 3)nn.init.kaiming_uniform_(linear.weight)print(linear.weight.data)# 7. xavier 初始化
def test07():# xavier 正態分布初始化linear = nn.Linear(5, 3)nn.init.xavier_normal_(linear.weight)print(linear.weight.data)# xavier 均勻分布初始化linear = nn.Linear(5, 3)nn.init.xavier_uniform_(linear.weight)print(linear.weight.data)if __name__ == '__main__':test07()

1.2 小節

網絡構建完成之后，我們需要對網絡參數進行初始化。常見的初始化方法有隨機初始化、全0初始化、全1初始化、Kaiming 初始化、Xavier 初始化等，一般我們在使用 PyTorch 構建網絡模型時，每個網絡層的參數都有默認的初始化方法，當然同學們也可以通過交給大家的方法來使用指定的方式對網絡參數進行初始化。

第二章、優化方法

傳統的梯度下降優化算法中，可能會碰到以下情況：

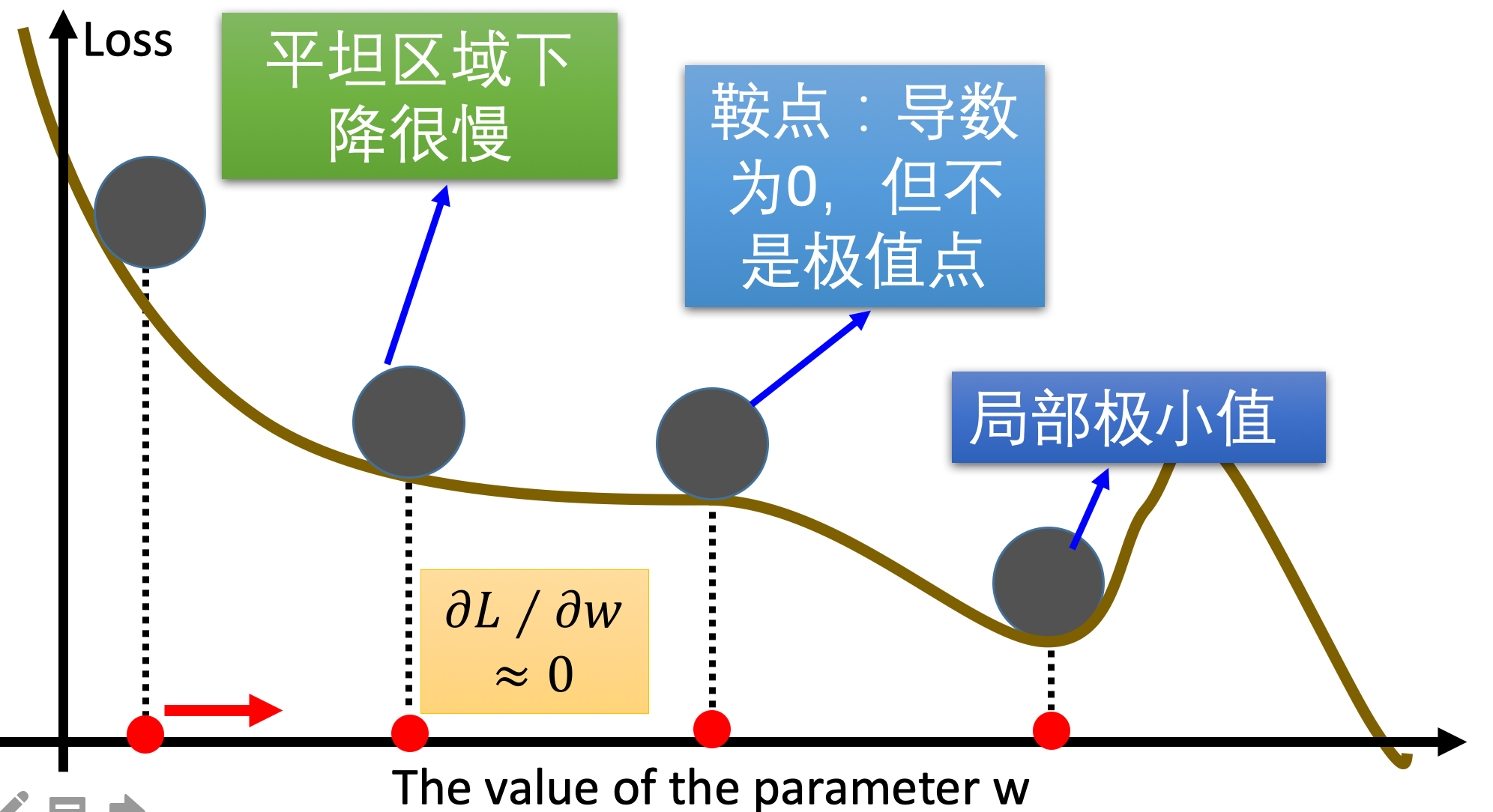
碰到平緩區域，梯度值較小，參數優化變慢碰到 “鞍點” ，梯度為 0，參數無法優化；
碰到局部最小值對于這些問題, 出現了一些對梯度下降算法的優化方法，例如：Momentum、AdaGrad、RMSprop、Adam 等。

下面解釋鞍點：
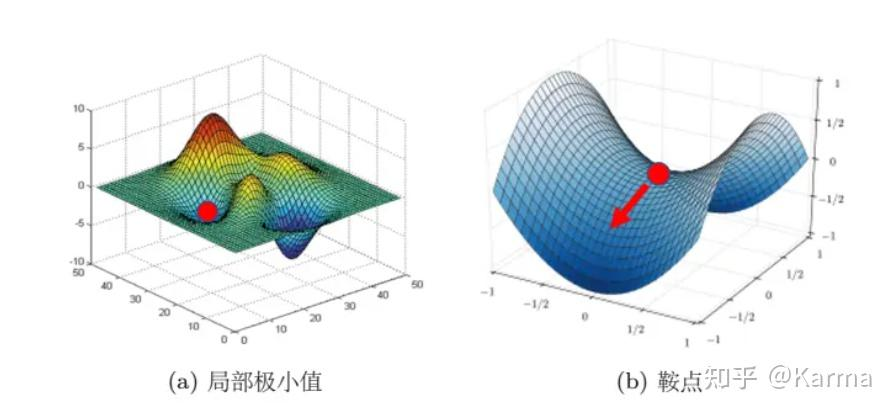
在這里插入圖片描述

鞍點（saddle point）與局部極小值點的區別：局部極小值為所在區域loss最小的點；鞍點所在區域還有可以讓loss下降的點，只要逃離鞍點，就有可能降低loss。

2.1 指數加權平均

我們最常見的算數平均指的是將所有數加起來除以數的個數，每個數的權重是相同的。加權平均指的是給每個數賦予不同的權重求得平均數。移動平均數，指的是計算最近鄰的 N 個數來獲得平均數。

指數移動加權平均則是參考各數值，并且各數值的權重都不同，距離越遠的數字對平均數計算的貢獻就越小（權重較小），距離越近則對平均數的計算貢獻就越大（權重越大）。

比如：明天氣溫怎么樣，和昨天氣溫有很大關系，而和一個月前的氣溫關系就小一些。

計算公式可以用下面的式子來表示：
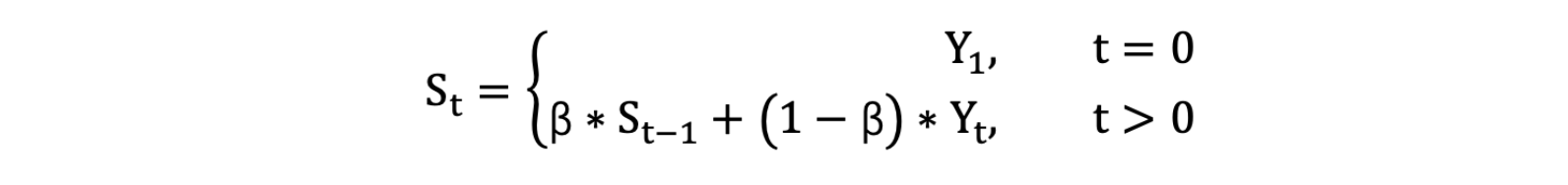
$S_t$ ：表示指數加權平均值;
$Y_t$ ：表示 t 時刻的值;
β 調節權重系數，該值越大平均數越平緩。

我們接下來通過一段代碼來看下結果，我們隨機產生進 30 天的氣溫數據：

import torch
import matplotlib.pyplot as pltELEMENT_NUMBER = 30# 1. 實際平均溫度
def test01():# 固定隨機數種子torch.manual_seed(0)# 產生30天的隨機溫度temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10print(temperature)# 繪制平均溫度days = torch.arange(1, ELEMENT_NUMBER + 1, 1)plt.plot(days, temperature, color='r')plt.scatter(days, temperature)plt.show()# 2. 指數加權平均溫度
def test02(beta=0.9):# 固定隨機數種子torch.manual_seed(0)# 產生30天的隨機溫度temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10print(temperature)exp_weight_avg = []for idx, temp in enumerate(temperature, 1):# 第一個元素的的 EWA 值等于自身if idx == 1:exp_weight_avg.append(temp)continue# 第二個元素的 EWA 值等于上一個 EWA 乘以 β + 當前氣氛乘以 (1-β)new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * tempexp_weight_avg.append(new_temp)days = torch.arange(1, ELEMENT_NUMBER + 1, 1)plt.plot(days, exp_weight_avg, color='r')plt.scatter(days, temperature)plt.show()if __name__ == '__main__':test01()test02(0.5)test02(0.9)

程序結果如下:

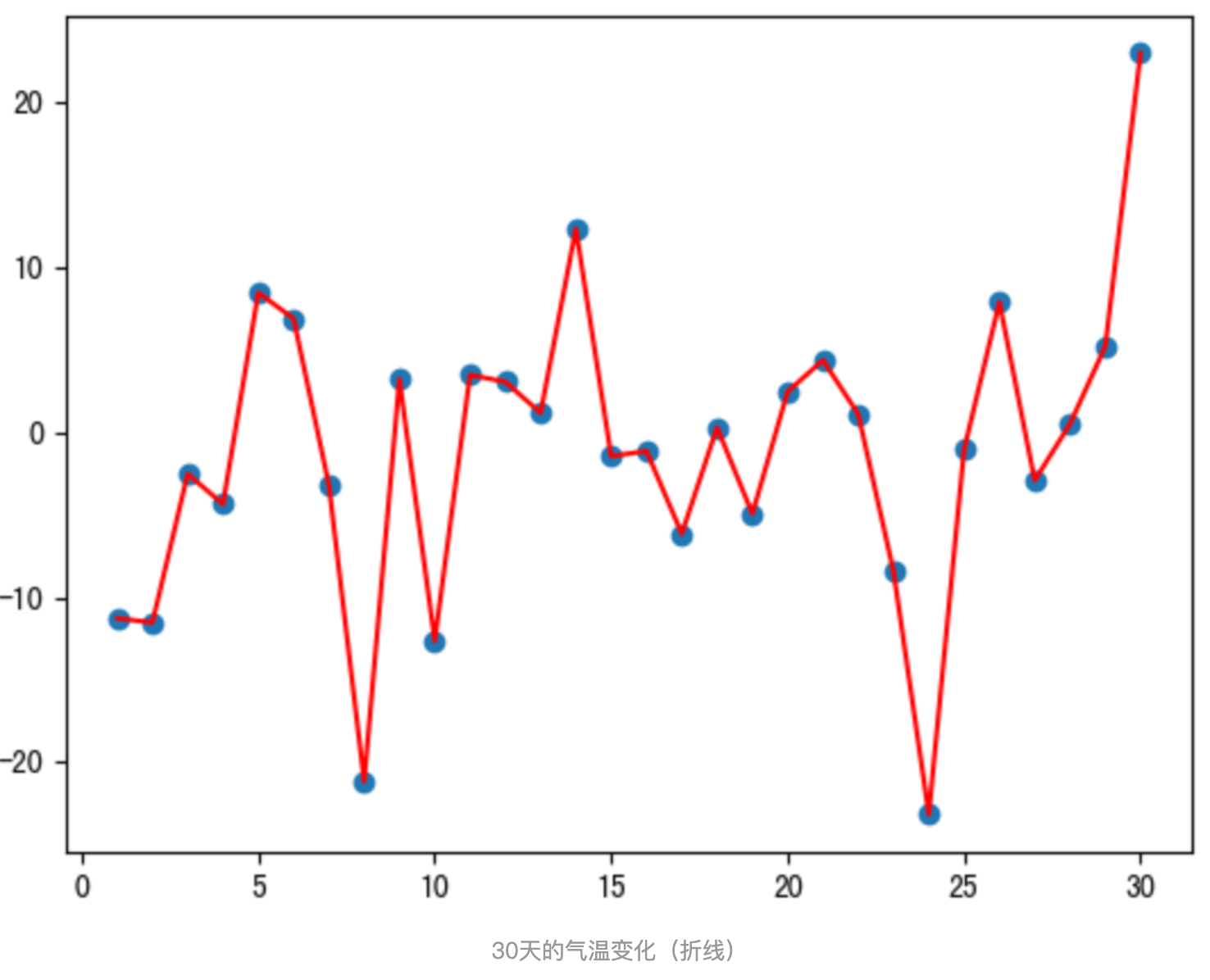
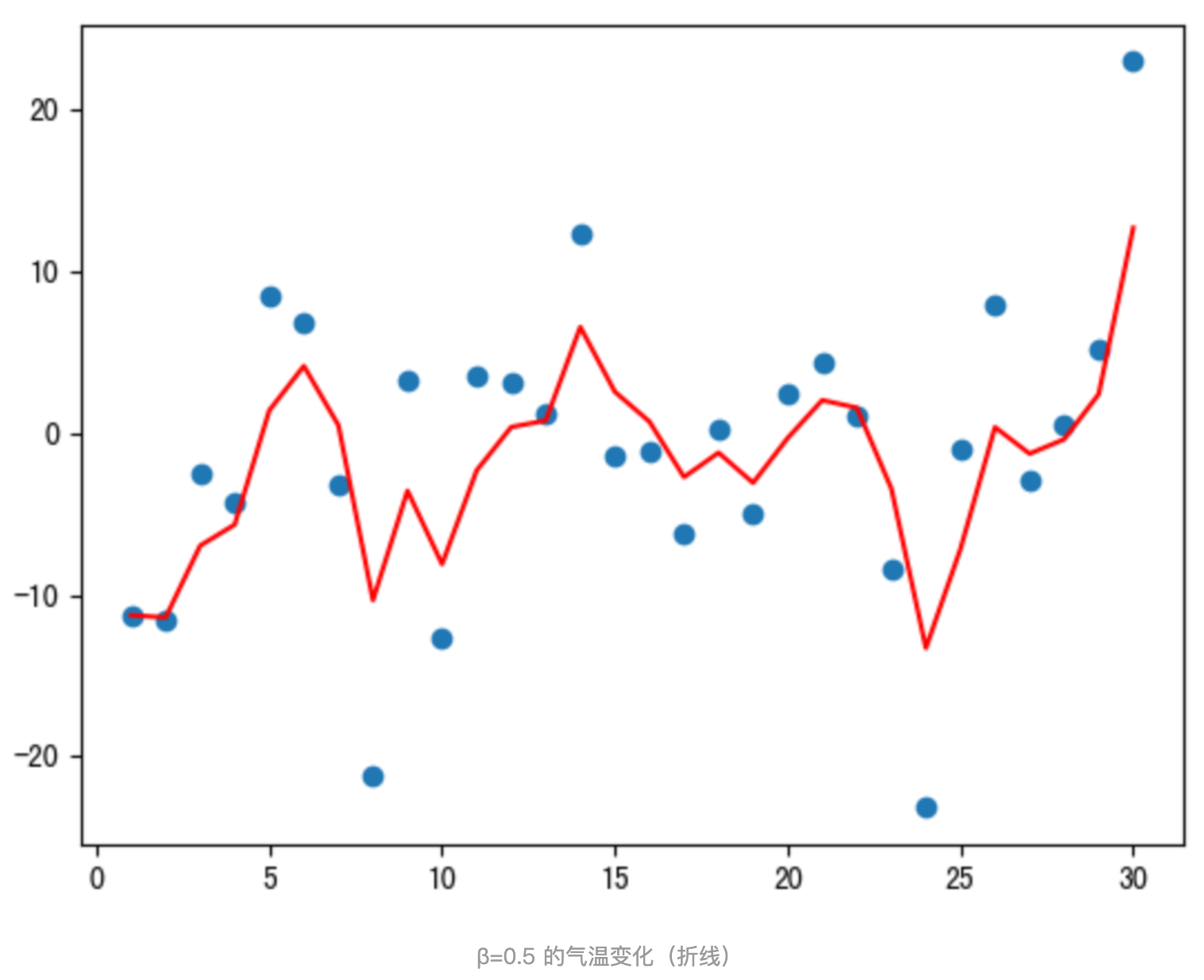
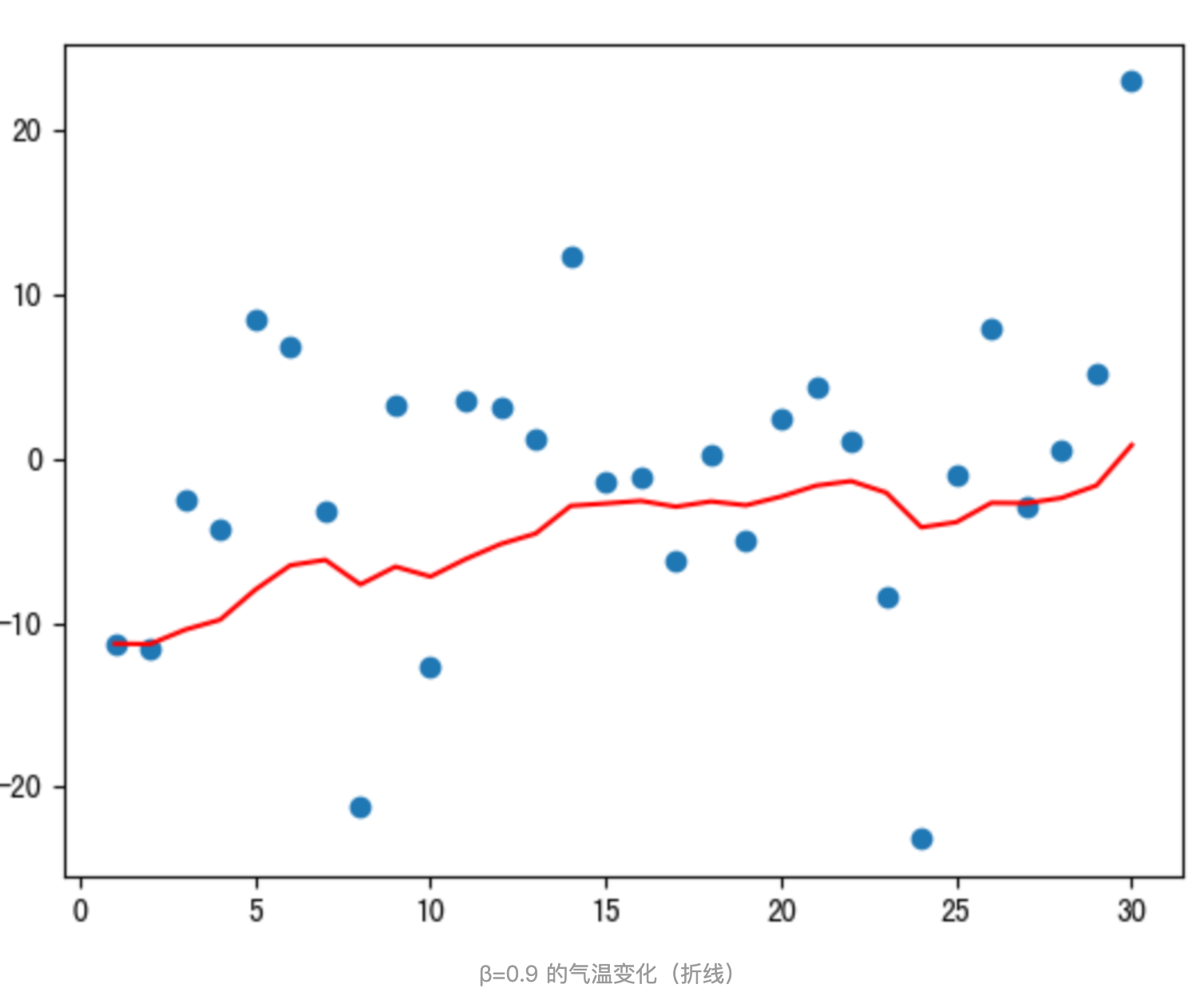
在這里插入圖片描述

從程序運行結果可以看到：

指數加權平均繪制出的氣氛變化曲線更加平緩; β 的值越大，則繪制出的折線越加平緩; β 值一般默認都是 0.9。

2.2 `Momentum`優化方法

當梯度下降碰到 “峽谷” 、”平緩”、”鞍點” 區域時, 參數更新速度變慢. Momentum 通過指數加權平均法，累計歷史梯度值，進行參數更新，越近的梯度值對當前參數更新的重要性越大。
在這里插入圖片描述

梯度計算公式： $D_t = β * S_{t-1}+ (1 - β) * D_t$

$S_{t-1}$ ：表示歷史梯度移動加權平均值
$D_t$ ：表示當前時刻的梯度值
β 為權重系數

咱們舉個例子，假設：權重 β 為 0.9，例如：第一次梯度值：s1 = d1 = w1，第二次梯度值：s2 = 0.9 + s1 + d2 * 0.1，第三次梯度值：s3 = 0.9 * s2 + d3 * 0.1，第四次梯度值：s4 = 0.9 * s3 + d4 * 0.1。

w 表示初始梯度
d 表示當前輪數計算出的梯度值
s 表示歷史梯度值

梯度下降公式中梯度的計算，就不再是當前時刻 t 的梯度值，而是歷史梯度值的指數移動加權平均值。公式修改為：

$W_{t+1} = W_t - a * D_t$

那么，Monmentum 優化方法是如何一定程度上克服 “平緩”、”鞍點”、”峽谷” 的問題呢？
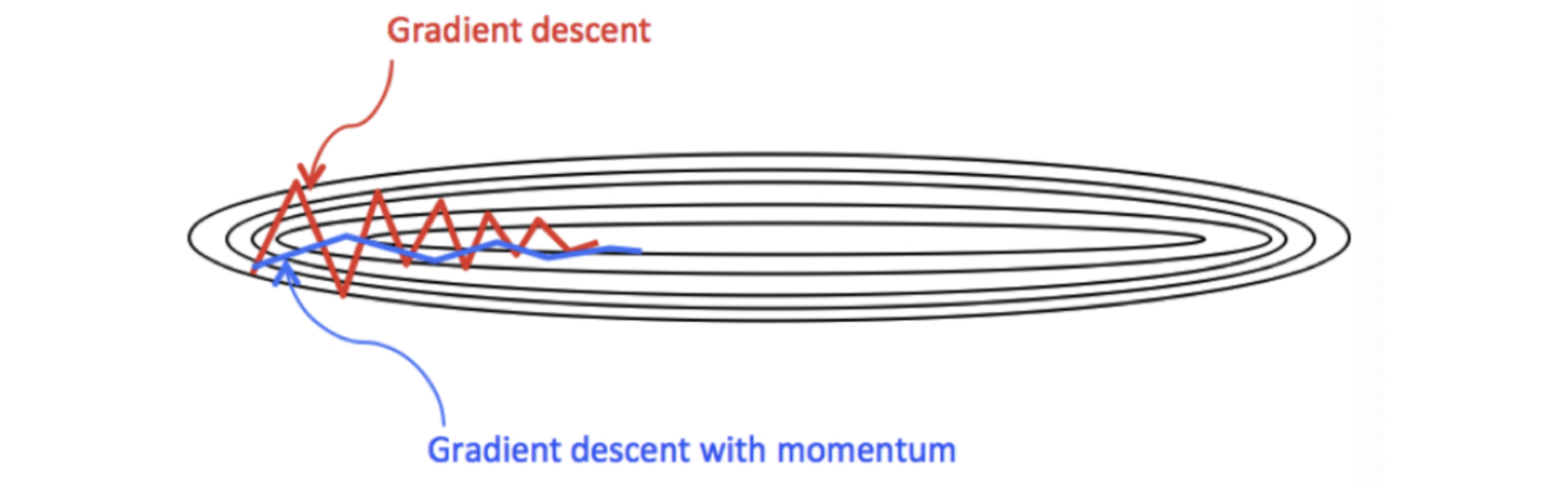
在這里插入圖片描述
當處于鞍點位置時，由于當前的梯度為 0，參數無法更新。但是 Momentum 動量梯度下降算法已經在先前積累了一些梯度值，很有可能使得跨過鞍點。

由于 mini-batch 普通的梯度下降算法，每次選取少數的樣本梯度確定前進方向，可能會出現震蕩，使得訓練時間變長。Momentum 使用移動加權平均，平滑了梯度的變化，使得前進方向更加平緩，有利于加快訓練過程。一定程度上有利于降低 “峽谷” 問題的影響。

峽谷問題：就是會使得參數更新出現劇烈震蕩。

Momentum 算法可以理解為是對梯度值的一種調整，我們知道梯度下降算法中還有一個很重要的學習率，Momentum 并沒有學習率進行優化。

2.3 AdaGrad優化方法

AdaGrad 通過對不同的參數分量使用不同的學習率，AdaGrad 的學習率總體會逐漸減小，這是因為 AdaGrad 認為：在起初時，我們距離最優目標仍較遠，可以使用較大的學習率，加快訓練速度，隨著迭代次數的增加，學習率逐漸下降。

其計算步驟如下：

初始化學習率 α、初始化參數 θ、小常數 σ = 1e-6
初始化梯度累積變量 s = 0
從訓練集中采樣 m 個樣本的小批量，計算梯度 g
累積平方梯度 s = s + g ⊙ g，⊙ 表示各個分量相乘
學習率 α 的計算公式如下：
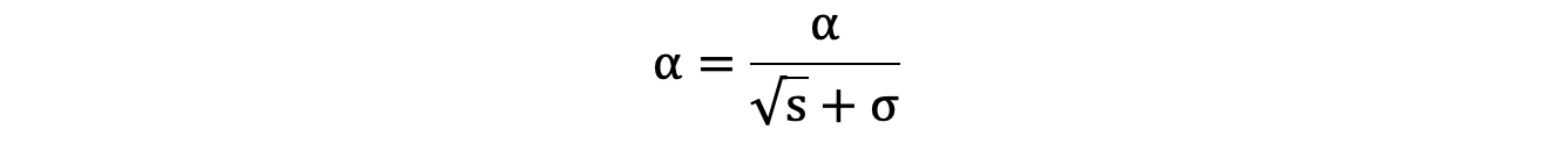
參數更新公式如下：
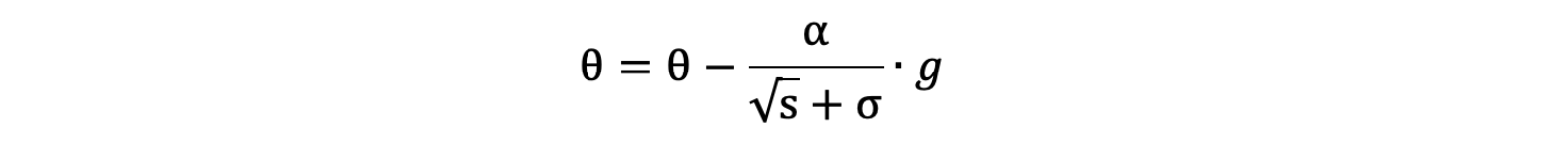
重復 2-7 步驟.
AdaGrad 缺點是可能會使得學習率過早、過量的降低，導致模型訓練后期學習率太小，較難找到最優解。

2.4 RMSProp優化方法

RMSProp 優化算法是對 AdaGrad 的優化. 最主要的不同是，其使用指數移動加權平均梯度替換歷史梯度的平方和。其計算過程如下：

初始化學習率 α、初始化參數 θ、小常數 σ = 1e-6
初始化參數 θ
初始化梯度累計變量 s
從訓練集中采樣 m 個樣本的小批量，計算梯度 g
使用指數移動平均累積歷史梯度，公式如下：
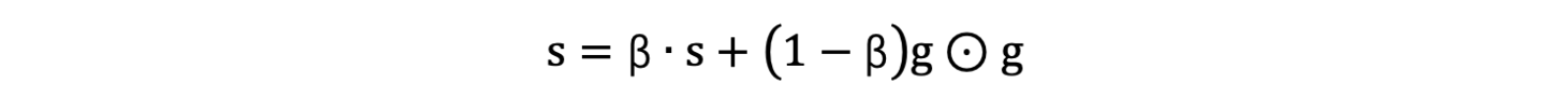
學習率 α 的計算公式如下：
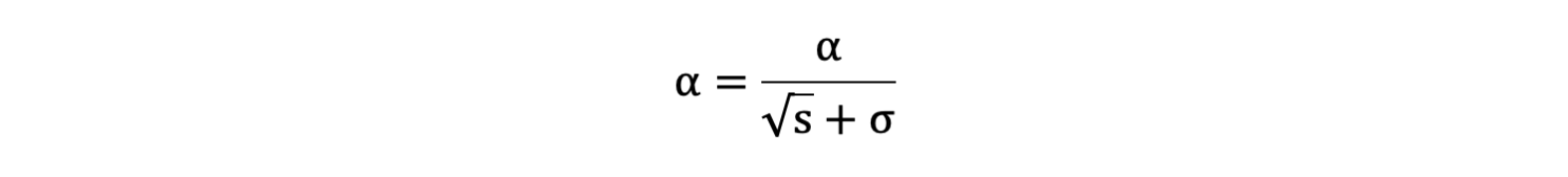
參數更新公式如下：

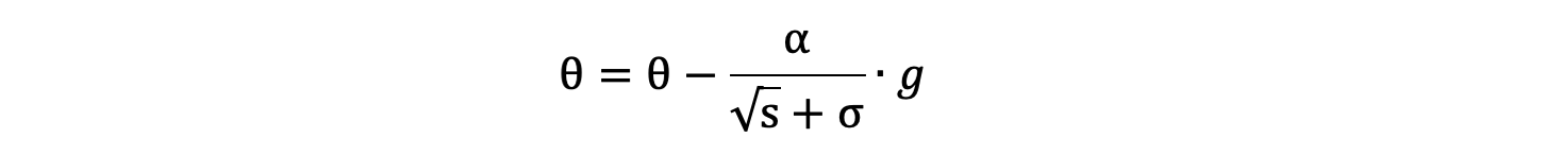
RMSProp 與 AdaGrad 最大的區別是對梯度的累積方式不同，對于每個梯度分量仍然使用不同的學習率。

RMSProp 通過引入衰減系數 β，控制歷史梯度對歷史梯度信息獲取的多少. 被證明在神經網絡非凸條件下的優化更好，學習率衰減更加合理一些。

需要注意的是：AdaGrad 和 RMSProp 都是對于不同的參數分量使用不同的學習率，如果某個參數分量的梯度值較大，則對應的學習率就會較小，如果某個參數分量的梯度較小，則對應的學習率就會較大一些。

2.5 Adam優化方法

Momentum 使用指數加權平均計算當前的梯度值、AdaGrad、RMSProp 使用自適應的學習率，Adam 結合了 Momentum、RMSProp 的優點，使用：移動加權平均的梯度和移動加權平均的學習率。使得能夠自適應學習率的同時，也能夠使用 Momentum 的優點。

2.6 小節

本小節主要學習了常見的一些對普通梯度下降算法的優化方法，主要有 Momentum、AdaGrad、RMSProp、Adam 等優化方法，其中 Momentum 使用指數加權平均參考了歷史梯度，使得梯度值的變化更加平緩。AdaGrad 則是針對學習率進行了自適應優化，由于其實現可能會導致學習率下降過快，RMSProp 對 AdaGrad 的學習率自適應計算方法進行了優化，Adam 則是綜合了 Momentum 和 RMSProp 的優點，在很多場景下，Adam 的表示都很不錯。

第三章、正則化

在訓深層練神經網絡時，由于模型參數較多，在數據量不足的情況下，很容易過擬合。Dropout 就是在神經網絡中一種緩解過擬合的方法。

3.1 `Dropout` 層的原理和使用

我們知道，緩解過擬合的方式就是降低模型的復雜度，而 Dropout 就是通過減少神經元之間的連接，把稠密的神經網絡神經元連接，變成稀疏的神經元連接，從而達到降低網絡復雜度的目的。

我們先通過一段代碼觀察下丟棄層的效果：

import torch
import torch.nn as nndef test():# 初始化丟棄層，p=0.8是以80%的概率舍去神經元dropout = nn.Dropout(p=0.8)# 初始化輸入數據inputs = torch.randint(0, 10, size=[5, 8]).float()print(inputs)print('-' * 50)outputs = dropout(inputs)print(outputs)if __name__ == '__main__':test()

程序輸出結果：

tensor([[1., 0., 3., 6., 7., 7., 5., 7.],[6., 8., 4., 6., 2., 0., 4., 1.],[1., 4., 6., 9., 3., 1., 2., 1.],[0., 6., 3., 7., 1., 7., 8., 9.],[5., 6., 8., 4., 1., 7., 5., 5.]])
--------------------------------------------------
tensor([[ 0.,  0., 15.,  0.,  0.,  0.,  0.,  0.],[ 0.,  0.,  0.,  0., 10.,  0.,  0.,  0.],[ 0.,  0.,  0., 45.,  0.,  0.,  0.,  0.],[ 0.,  0., 15.,  0.,  0.,  0.,  0.,  0.],[25.,  0.,  0.,  0.,  0.,  0.,  0., 25.]])

我們將 Dropout 層的概率 p 設置為 0.8，此時經過 Dropout 層計算的張量中就出現了很多 0，（神經元失效在張量上的體現就是0），概率 p 設置值越大，則張量中出現的 0 就越多。

上面結果的計算過程如下：

先按照 p 設置的概率，隨機將部分的張量元素設置為 0；
為了校正張量元素被設置為 0 帶來的影響，需要對非 0 的元素進行縮放，其縮放因子為: 1/(1-p)，上面代碼中 p 的值為 0.8，根據公式縮放因子為：1/(1-0.8) = 5；
比如：第 3 個元素，原來是 3，乘以縮放因子之后變成 15。

我們也發現了，丟棄概率 p 的值越大，則縮放因子的值就越大，相對其他未被設置的元素就要更多的變大。丟棄概率 P 的值越小，則縮放因子的值就越小，相對應其他未被置為 0 的元素就要有較小的變大。

當張量某些元素被設置為 0 時，對網絡會帶來什么影響？

模型中神經元失效，導致模型變笨。

比如上面這種情況，如果輸入Dropout 后的樣本，會使得某些參數無法更新，請看下面的代碼：

import torch
import torch.nn as nn# 設置隨機數種子
torch.manual_seed(0)def caculate_gradient(x, w):y = x @ wy = y.sum()y.backward()print('Gradient:', w.grad.reshape(1, -1).squeeze().numpy())def test01():# 初始化權重w = torch.randn(15, 1, requires_grad=True)# 初始化輸入數據x = torch.randint(0, 10, size=[5, 15]).float()# 計算梯度caculate_gradient(x, w)def test02():# 初始化權重w = torch.randn(15, 1, requires_grad=True)# 初始化輸入數據x = torch.randint(0, 10, size=[5, 15]).float()# 初始化丟棄層dropout = nn.Dropout(p=0.8)x = dropout(x)# 計算梯度caculate_gradient(x, w)if __name__ == '__main__':test01()print('-' * 70)test02()

程序輸出結果:

Gradient: [19. 15. 16. 13. 34. 23. 20. 22. 23. 26. 21. 29. 28. 22. 29.]
----------------------------------------------------------------------
Gradient: [ 5.  0. 35.  0.  0. 45. 40. 40.  0. 20. 25. 45. 55.  0. 10.]

從程序結果來看，是否經過 Dropout 層對梯度的計算產生了不小的影響，例如：經過 Dropout 層之后有一些梯度為 0，這使得參數無法得到更新，從而達到了降低網絡復雜度的目的。

第四章、批量歸一化

在神經網絡的搭建過程中，Batch Normalization （批量歸一化）是經常使用一個網絡層，其主要的作用是控制數據的分布，加快網絡的收斂。

我們知道，神經網絡的學習其實在學習數據的分布，隨著網絡的深度增加、網絡復雜度增加，一般流經網絡的數據都是一個 mini batch，每個 mini batch 之間的數據分布變化非常劇烈，這就使得網絡參數頻繁的進行大的調整以適應流經網絡的不同分布的數據，給模型訓練帶來非常大的不穩定性，使得模型難以收斂。

如果我們對每一個 mini batch 的數據進行標準化之后，數據分布就變得穩定，參數的梯度變化也變得穩定，有助于加快模型的收斂。

4.1 批量歸一化公式

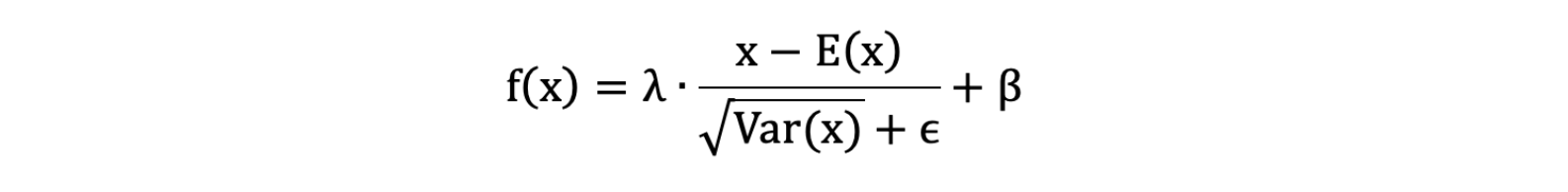
在這里插入圖片描述

λ 和 β 是可學習的參數，它相當于對標準化后的值做了一個線性變換，λ 為系數，β 為偏置；
eps ：通常指為 1e-5，避免分母為 0；
E(x) ：表示變量的均值；
Var(x)：表示變量的方差；

數據在經過 BN 層之后，無論數據以前的分布是什么，都會被歸一化成均值為 β，標準差為 γ 的分布。

注意：BN 層不會改變輸入數據的維度，只改變輸入數據的的分布。在實際使用過程中，BN 常常和卷積神經網絡結合使用，卷積層的輸出結果后接 BN 層。

4.2 BN 層的接口

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True)

由于每次使用的 mini batch 的數據集，所以 BN 使用移動加權平均來近似計算均值和方差，而 momentum 參數則調節移動加權平均值的計算；
affine = False：表示 γ=1，β=0，反之，則表示 γ 和 β 要進行學習;
BatchNorm2d ：適用于輸入的數據為 4D，輸入數據的形狀 [N,C,H,W]
其中：N 表示批次，C 代表通道數，H 代表高度，W 代表寬度

由于每次輸入到網絡中的是小批量的樣本，我們使用指數加權平均來近似表示整體的樣本的均值和方法，其更新公式如下：

running_mean = momentum * running_mean + (1.0 – momentum) * batch_mean
running_var = momentum * running_var + (1.0 – momentum) * batch_var

上面的式子中，batch_mean 和 batch_var 表示當前批次的均值和方差。而 running_mean 和 running_var 是近似的整體的均值和方差的表示。當我們進行評估時，可以使用該均值和方差對輸入數據進行歸一化。

第五章、案例-價格分類

小明創辦了一家手機公司，他不知道如何估算手機產品的價格。為了解決這個問題，他收集了多家公司的手機銷售數據。

我們需要幫助小明找出手機的功能（例如：RAM等）與其售價之間的某種關系。我們可以使用機器學習的方法來解決這個問題，也可以構建一個全連接的網絡。

全連接網絡：當前第 n 層的神經元全部與 n-1 層的神經元連接；

需要注意的是: 在這個問題中，我們不需要預測實際價格，而是一個價格范圍，它的范圍使用 0、1、2、3 來表示，所以該問題也是一個分類問題。

5.1 構建數據集

數據共有 2000 條, 其中 1600 條數據作為訓練集, 400 條數據用作測試集。我們使用 sklearn 的數據集劃分工作來完成。并使用 PyTorch 的 TensorDataset 來將數據集構建為 Dataset 對象，方便構造數據集加載對象。

# 構建數據集
def create_dataset():data = pd.read_csv('data/手機價格預測.csv')# 特征值x和目標值y，iloc()根據索引取值x, y = data.iloc[:, :-1], data.iloc[:, -1]x = x.astype(np.float32)y = y.astype(np.int64)# 數據集劃分x_train, x_valid, y_train, y_valid = \train_test_split(x, y, train_size=0.8, random_state=88, stratify=y)# 構建數據集（必須是tensor類型）train_dataset = TensorDataset(torch.from_numpy(x_train.values), torch.tensor(y_train.values))valid_dataset = TensorDataset(torch.from_numpy(x_valid.values), torch.tensor(y_valid.values))# x_train.shape[0]代表函數，x_train.shape[0]代表列數return train_dataset, valid_dataset, x_train.shape[1], len(np.unique(y))train_dataset, valid_dataset, input_dim, class_num = create_dataset()

train_test_split 是 scikit-learn 庫中用于將數據集分割為訓練集和測試集的函數。下面我將詳細解釋你提到的每個參數的含義：

x: 這是輸入特征的數組或矩陣。通常，x 包含你想要用于訓練模型的所有特征數據。
y: 這是目標變量的數組。y 包含與 x 中的每個樣本相對應的標簽或目標值。
train_size: 這個參數指定訓練集的比例。在這個例子中，train_size=0.8 意味著 80% 的數據將被用作訓練集，剩下的 20% 將用作測試集。
random_state: 這個參數用于設置隨機數生成器的種子，確保每次運行代碼時分割的結果都是一致的。在這個例子中，random_state=88 意味著使用種子 88 來初始化隨機數生成器。
stratify: 這個參數用于分層抽樣。在這個例子中，stratify=y 意味著訓練集和測試集中的目標變量 y 的類別分布將與原始數據集中的類別分布保持一致。這對于確保訓練集和測試集具有相似的類別比例非常有用，特別是在處理不平衡數據集時。

5.2 構建分類網絡模型

我們構建的用于手機價格分類的模型叫做全連接神經網絡。它主要由三個線性層來構建，在每個線性層后，我們使用的時 sigmoid 激活函數。

# 構建網絡模型
class PhonePriceModel(nn.Module):def __init__(self, input_dim, output_dim):super(PhonePriceModel, self).__init__()# nn.Linear(n1, n2)構建全連接層，n1為輸入的神經元個數，n2為輸出的神經元個數# self.linear1()為第1層網絡self.linear1 = nn.Linear(input_dim, 128)# self.linear2()為第2層網絡，其輸入的神經元個數必須等于第一層輸出的神經元個數self.linear2 = nn.Linear(128, 256)self.linear3 = nn.Linear(256, output_dim)# 定義激活函數，使用sigmoid函數def _activation(self, x):return torch.sigmoid(x)# 前向傳播的邏輯必須自己寫def forward(self, x):# 將第1層的輸出經過激活函數x = self._activation(self.linear1(x))# 將第2層的輸出經過激活函數x = self._activation(self.linear2(x))# 第3層的輸出層直接輸出output = self.linear3(x)return output

我們的網絡共有 3 個全連接層, 具體信息如下:

第一層: 輸入為維度為 20, 輸出維度為: 128
第二層: 輸入為維度為 128, 輸出維度為: 256
第三層: 輸入為維度為 256, 輸出維度為: 4

注意：由于手機價格為 0、 1、 2、 3共計4類，故需要最后的網絡輸出為4個神經元；

5.3 編寫訓練函數

網絡編寫完成之后，我們需要編寫訓練函數。

所謂的訓練函數，指的是輸入數據讀取、送入網絡、計算損失、更新參數的流程，該流程較為固定。我們使用的是多分類交叉生損失函數、使用 SGD 優化方法。最終，將訓練好的模型持久化到磁盤中。

def train():# 固定隨機數種子torch.manual_seed(0)# 初始化模型model = PhonePriceModel(input_dim, class_num)# 損失函數（交叉熵損失函數）criterion = nn.CrossEntropyLoss()# 優化方法（SGD隨機梯度下降）optimizer = optim.SGD(model.parameters(), lr=1e-3)# 訓練輪數num_epoch = 50# 雙層經典循環：外層epoch輪次循環，內層dataloader循環for epoch_idx in range(num_epoch):# 初始化數據加載器，shuffle=True：將數據集打散，不按照之前的數據順序# batch_size=8：每次將8個樣本輸入到模型dataloader = DataLoader(train_dataset, shuffle=True, batch_size=8)# 訓練時間start = time.time()# 計算損失total_loss = 0.0total_num = 1# 準確率correct = 0# 遍歷數據集for x, y in dataloader:output = model(x)# 計算損失loss = criterion(output, y)# 梯度清零optimizer.zero_grad()# 反向傳播loss.backward()# 參數更新optimizer.step()total_num += len(y)total_loss += loss.item() * len(y)print('epoch: %4s loss: %.2f, time: %.2fs' %(epoch_idx + 1, total_loss / total_num, time.time() - start))# 模型保存torch.save(model.state_dict(), 'model/phone-price-model.bin')

模型訓練就固定3個大步驟：

實例化模型 module = nn.Module() 類對象
選定損失函數 nn.CrossEntropyLoss()
選定優化器 nn.optim.SGD() 、nn.optim.Adam()

經典的雙層循環：

外層循環指定訓練次數
內層循環中老三樣：1）梯度清零 optimizer.zero_grad()；2）反向傳播 loss.backward()；3）參數更新 optimizer.step()

5.4 編寫評估函數

評估函數、也叫預測函數、推理函數，主要使用訓練好的模型，對未知的樣本的進行預測的過程。我們這里使用前面單獨劃分出來的測試集來進行評估。

def test():# 加載模型model = PhonePriceModel(input_dim, class_num)model.load_state_dict(torch.load('model/phone-price-model.bin'))# 構建加載器，驗證集中的數據一般不需要打散，故shuffle=Falsedataloader = DataLoader(valid_dataset, batch_size=8, shuffle=False)# 評估測試集correct = 0for x, y in dataloader:output = model(x)# 得到的output為4分類的概率：[0.12, 0.25, 0.56, 0.12, 0.07]，需要找出其中最大的y_pred = torch.argmax(output, dim=1)# 如果預預測值等于真實值，那么就累加1次correct += (y_pred == y).sum()print('Acc: %.5f' % (correct.item() / len(valid_dataset)))

程序輸出結果:

Acc: 0.54750

5.5 網絡性能調優

我們前面的網絡模型在測試集的準確率為: 0.54750, 我們可以通過以下方面進行調優:

對輸入數據進行標準化
調整優化方法
調整學習率
增加批量歸一化層
增加網絡層數、神經元個數
增加訓練輪數
等等…

我進行下如下調整：

優化方法由 SGD 調整為 Adam
學習率由 1e-3 調整為 1e-4
對數據數據進行標準化
增加網絡深度, 即: 增加網絡參數量

網絡模型在測試集的準確率由 0.5475 上升到 0.9625，調整后的完整代碼為:

import torch
import torch.nn as nn
import torch.nn.functional as F
import pandas as pd
from sklearn.model_selection import train_test_split
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import torch.optim as optim
import numpy as np
import time
from sklearn.preprocessing import StandardScaler# 構建數據集
def create_dataset():data = pd.read_csv('data/手機價格預測.csv')# 特征值和目標值x, y = data.iloc[:, :-1], data.iloc[:, -1]x = x.astype(np.float32)y = y.astype(np.int64)# 數據集劃分x_train, x_valid, y_train, y_valid = \train_test_split(x, y, train_size=0.8, random_state=88, stratify=y)# 數據標準化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_valid = transfer.transform(x_valid)# 構建數據集train_dataset = TensorDataset(torch.from_numpy(x_train), torch.tensor(y_train.values))valid_dataset = TensorDataset(torch.from_numpy(x_valid), torch.tensor(y_valid.values))return train_dataset, valid_dataset, x_train.shape[1], len(np.unique(y))train_dataset, valid_dataset, input_dim, class_num = create_dataset()# 構建網絡模型
class PhonePriceModel(nn.Module):def __init__(self, input_dim, output_dim):super(PhonePriceModel, self).__init__()self.linear1 = nn.Linear(input_dim, 128)self.linear2 = nn.Linear(128, 256)self.linear3 = nn.Linear(256, 512)self.linear4 = nn.Linear(512, 128)self.linear5 = nn.Linear(128, output_dim)def _activation(self, x):return torch.sigmoid(x)def forward(self, x):x = self._activation(self.linear1(x))x = self._activation(self.linear2(x))x = self._activation(self.linear3(x))x = self._activation(self.linear4(x))output = self.linear5(x)return output# 編寫訓練函數
def train():# 固定隨機數種子torch.manual_seed(0)# 初始化模型model = PhonePriceModel(input_dim, class_num)# 將模型加載到GPU上提升訓練速度，兩種方法都可以# model = module.cuda()# module = module.to('cuda')# 損失函數criterion = nn.CrossEntropyLoss()# 優化方法optimizer = optim.Adam(model.parameters(), lr=1e-4)# 訓練輪數num_epoch = 50for epoch_idx in range(num_epoch):# 初始化數據加載器dataloader = DataLoader(train_dataset, shuffle=True, batch_size=8)# 訓練時間start = time.time()# 計算損失total_loss = 0.0total_num = 1# 準確率correct = 0for x, y in dataloader:# x = x.to()			# 如有GPU，可以將數據加載到GPU# y = y.to()			# 如有GPU，可以將數據加載到GPUoutput = model(x)# 計算損失loss = criterion(output, y)# 梯度清零optimizer.zero_grad()# 反向傳播loss.backward()# 參數更新optimizer.step()total_num += len(y)total_loss += loss.item() * len(y)print('epoch: %4s loss: %.2f, time: %.2fs' %(epoch_idx + 1, total_loss / total_num, time.time() - start))# 模型保存torch.save(model.state_dict(), 'model/phone-price-model.bin')def test():# 加載模型model = PhonePriceModel(input_dim, class_num)model.load_state_dict(torch.load('model/phone-price-model.bin'))# 構建加載器dataloader = DataLoader(valid_dataset, batch_size=8, shuffle=False)# 評估測試集correct = 0for x, y in dataloader:output = model(x)y_pred = torch.argmax(output, dim=1)correct += (y_pred == y).sum()print('Acc: %.5f' % (correct.item() / len(valid_dataset)))if __name__ == '__main__':train()test()