Lipschitz function
一、說明
在數學分析中,Lipschitz連續性以德國 數學家 魯道夫·利普希茨 (Rudolf Lipschitz)的名字命名,是函數一致連續性的強形式。直觀地說,Lipschitz連續函數的變化速度有限:存在一個實數,使得對于該函數圖上的每一對點,連接它們的直線斜率的絕對值不大于該實數;這樣的最小邊界稱為該函數的Lipschitz常數(與一致連續模相關)。例如,每個定義在區間上且具有有界的一階導數的函數都是Lipschitz連續的。
二、關于
2.1 定義
Lipschitz function函數f 如下
∣f(x)?f(y)∣<=C∣x?y∣|f(x)-f(y)|<=C|x-y|∣f(x)?f(y)∣<=C∣x?y∣
對于所有x 和y,其中C是與x和y無關的常數,稱為利普希茨函數。
-
任何具有有界的一階導數的函數必定是利普希茨函數。
顯然,所有的直線函數都是Lipschitz function函數。 -
利普希茨連續性并不是說你可以隨便取任意的x和y,并繪制|f(x) - f(y)| ≤ M|x - y|。它說的是M是固定的,且不等式對所有x, y ∈ R都成立。
這是一個更強的條件。如果你只需要為每個x和y選擇一個M,那么這個條件將毫無意義。
2.2 一些討論
① 二次拋物線函數不是Lipschitz函數
假如y=x2y=x^2y=x2
因為,對于等差序列x1,x2,x3∈Rx_1,x_2,x_3∈Rx1?,x2?,x3?∈R,0<x1<x2<x30<x_1<x_2<x_30<x1?<x2?<x3?,那么
∣y1?y2∣=∣x12?x22∣<=C1∣x1?x2∣|y_1-y_2|=|x_1^2-x_2^2|<=C1|x_1 - x_2|∣y1??y2?∣=∣x12??x22?∣<=C1∣x1??x2?∣
∣x1+x2∣<=C1|x_1 +x_2 |<=C1∣x1?+x2?∣<=C1
同樣:
∣y2?y3∣=∣x22?x32∣<=C1∣x2?x3∣|y_2-y_3|=|x_2^2-x_3^2|<=C1|x_2 - x_3|∣y2??y3?∣=∣x22??x32?∣<=C1∣x2??x3?∣
∣x2+x3∣<=C2|x_2 +x_3 |<=C2∣x2?+x3?∣<=C2
顯然C1<C2C_1<C_2C1?<C2?,即隨著x的遞增,C也是遞增的
隨著x1<x2<x3→∞x_1<x_2<x_3 \to \inftyx1?<x2?<x3?→∞也有C∞→∞C_{\infty} \to \inftyC∞?→∞
也就是在函數的全定義域內,沒有一個固定的C使的∣f(x)?f(y)∣<=C∣x?y∣|f(x)-f(y)|<=C|x-y|∣f(x)?f(y)∣<=C∣x?y∣
② 利普希茨連續且處處可微的函數
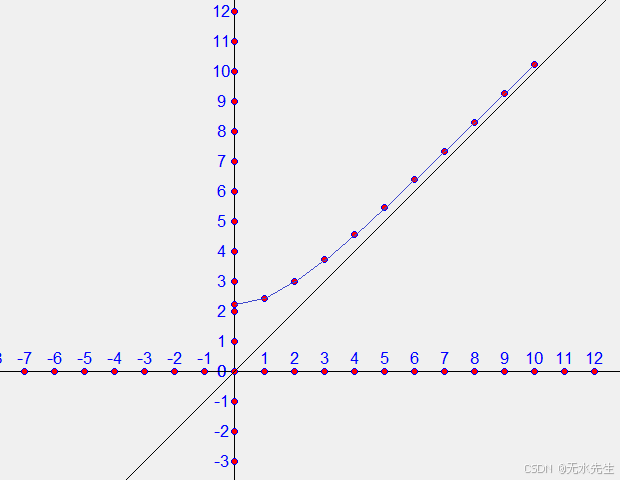
雙曲函數:

對所有實數定義的是 Lipschitz 連續的,且 Lipschitz 常數K = 1,因為它處處可微,且導數的絕對值在 1 以上有界。請參閱下面“屬性”下列出的第一個屬性。
③ Lipschitz 連續函數并非處處可微
函數
f(x)=∣x∣f(x)=|x|f(x)=∣x∣
是在實數上定義的范數是Lipschitz連續的,Lipschitz常數等于1,由反三角不等式定義。更一般地,向量空間上的范數關于相關度量是Lipschitz連續的,Lipschitz常數等于1。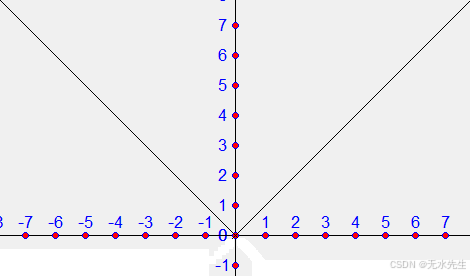
,注意:在x=0處不可微。
④處處可微但非連續可微的 Lipschitz 連續函數
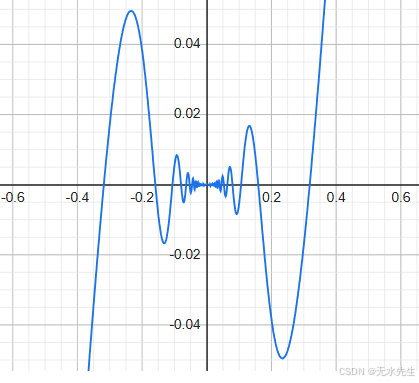
函數
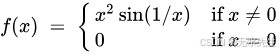
其導數存在,但在x=0{\displaystyle x=0}x=0不能連續
三、綜合
如果你的函數是可微的,Lipschitz 連續性只是說這個函數的導數是有界的。我認為這是對“抖動”和“拉伸”的限制。
或者拉伸,它說一個函數 f:R→Rf: \mathbb{R} \to \mathbb{R}f:R→R 不能增長得太快。例如,如果Lipschitz常數是1且(f(0)=0),那么它被夾在兩條直線 (y=x) 和 (y=-x) 之間。這基本上意味著它不能增長得過快,也不能搖擺太多。
如果常數 M 小于 1,那么這個函數被稱為收縮函數,它具有許多良好的性質。







)











的硬件組件及其應用注意事項)