OpenCV圖像梯度、邊緣檢測、輪廓繪制、凸包檢測大合集

一、圖像梯度

在圖像處理中，「梯度（Gradient）」是一個非常基礎但又極其重要的概念。它是圖像邊緣檢測、特征提取、紋理分析等眾多任務的核心。梯度的本質是在空間上描述像素灰度值變化的快慢和方向。

但我們如何在圖像中計算梯度？又該選擇什么樣的算子？本文將從梯度的數學定義出發，逐步引入經典的 Sobel 與 Laplacian 算子，帶你了解圖像梯度的計算原理與實踐方式。

1.1 什么是圖像梯度？

圖像梯度反映的是像素值（灰度或強度）在空間中的變化率。可以類比為地形圖中的“坡度”：哪里灰度變化劇烈，哪里就是圖像的“邊緣”。

對于二維灰度圖像 $I (x, y)$ ，梯度定義為圖像對空間坐標的偏導數組成的向量：
$\nabla I = \left[ \frac{\partial I}{\partial x}, \frac{\partial I}{\partial y} \right]$

$?I?x\frac{\partial I}{\partial x}$ ：表示圖像在水平方向（x軸）上的變化率；
$?I?y\frac{\partial I}{\partial y}$ ：表示圖像在垂直方向（y軸）上的變化率。

該向量的模長表示梯度的強度，方向表示灰度變化最劇烈的方向。

1.2 如何計算梯度

由于圖像是離散的，我們不能直接求導，而是通過離散卷積實現近似求導

使用cv2.filter2D自定義卷積核

OpenCV中filter2D可以對圖形施加自定義的卷積核，是實現梯度算子的基礎方法

語法如下所示：

dst = cv2.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])

filter2D函數是用于對圖像進行二維卷積（濾波）操作。它允許用戶自定義卷積核（kernal）來實現各種圖像處理效果，如平滑，銳化，邊緣檢測。

參數解析：

參數名	類型	說明
`src`	`ndarray`	輸入圖像，必須是單通道或多通道（如灰度圖或彩色圖）
`ddepth`	`int`	輸出圖像的深度（如 `cv2.CV_64F`, `-1` 表示與原圖相同）
`kernel`	`ndarray`	卷積核（濾波器），必須是浮點型 `np.float32` 或 `np.float64`
`dst`	`ndarray`	（可選）輸出圖像，與 `src` 同大小
`anchor`	`tuple`	卷積核錨點，默認 `(-1, -1)` 表示核中心
`delta`	`float`	可選偏移值，加到卷積結果上
`borderType`	`int`	邊界填充方式，常見如 `cv2.BORDER_DEFAULT`（邊界反射_101）, `cv2.BORDER_REPLICATE`

import cv2 as cv
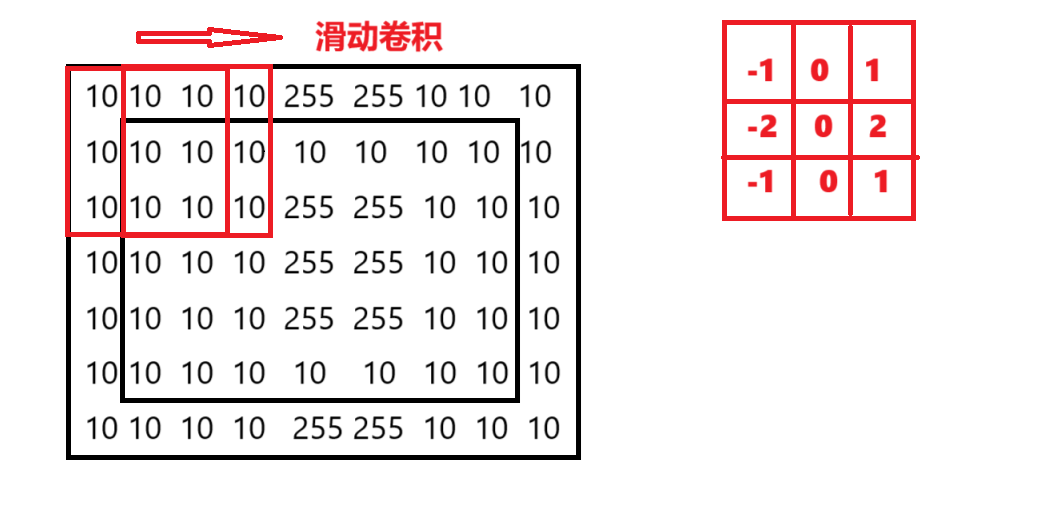
import numpy as np# 構造圖像：中心有明顯亮度突變
img = np.array([[10, 10, 10, 10, 10, 10, 10],[10, 10, 10, 255, 255, 10, 10],[10, 10, 10, 255, 255, 10, 10],[10, 10, 10, 255, 255, 10, 10],[10, 10, 10, 10, 10, 10, 10]
], dtype=np.uint8)# 使用 Sobel 水平方向邊緣檢測核
kernel = np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]], dtype=np.float32)# 卷積
img2 = cv.filter2D(img, -1, kernel)print(img2)

結果展示：

[[  0   0 255 255   0   0   0][  0   0 255 255   0   0   0][  0   0 255 255   0   0   0][  0   0 255 255   0   0   0][  0   0 255 255   0   0   0]]

滑動卷積

1.3 常見的梯度算子

1?? Sobel 算子（Sobel Operator）

Sobel 是最常見的梯度算子之一，結合了高斯平滑與微分運算，對噪聲更魯棒。

水平方向梯度核：

$Gx=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}$

垂直方向梯度核：
$G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$

在 OpenCV 中的實現：

語法說明：

dst = cv2.Sobel(src, ddepth, dx, dy, ksize=3, scale=1, delta=0, borderType=cv2.BORDER_DEFAULT)

參數名	類型	說明
`src`	`ndarray`	輸入圖像（通常為灰度圖）
`ddepth`	`int`	輸出圖像的數據深度（OpenCV 中，-1 表示輸出圖像的深度與輸入圖像相同。）
`dx`	`int`	x 方向求導階數（1 表示對 x 求一階導），獲取的垂直邊緣
`dy`	`int`	y 方向求導階數，獲取的水平邊緣
`ksize`	`int`	Sobel 核大小（可為 1, 3, 5, 7，常用 3）
`scale`	`float`	可選縮放因子，對導數結果進行縮放（一般為 1）
`delta`	`float`	可選偏移量，結果加上 delta（一般為 0）
`borderType`	`int`	邊界填充方式，默認 `cv2.BORDER_DEFAULT`

示例代碼：Sobel算子的使用

# sobel算子import cv2 as cvshudu = cv.imread('../images/shudu.png', cv.IMREAD_GRAYSCALE)# x方向
dst_x = cv.Sobel(shudu, -1, 1, 0, ksize=3)# y方向
dst_y = cv.Sobel(shudu, -1, 0, 1, ksize=3)# x和y方向
dst_xy = cv.Sobel(shudu, -1, 1, 1, ksize=3)cv.imshow('shudu', shudu)
cv.imshow('dst_x', dst_x)
cv.imshow('dst_y', dst_y)
cv.imshow('dst_xy', dst_xy)
cv.waitKey(0)
cv.destroyAllWindows()

結果輸出：


灰度圖	dx=1，dy=0（獲取垂直邊緣）	dx=0，dy=1（獲取水平邊緣）	dx=1,dy=1(不建議使用)，用Laplacian來獲取水平垂直邊緣。

dx，dy可以都為1，獲取的垂直和水平方向上的梯度。dx，dy不能都為0。

grad_x: 圖像在 x 方向的梯度（橫向變化）
grad_y: 圖像在 y 方向的梯度（縱向變化）

我們可以將它們組成一個向量：
$G?=(grad_x,?grad_y) \vec{G} = (grad\_x, \, grad\_y)$
然后，使用勾股定理計算這個向量的長度（也就是梯度強度）：
$magnitude=grad_x2+grad_y2 \text{magnitude} = \sqrt{grad\_x^2 + grad\_y^2}$

2?? Laplacian 算子（Laplacian Operator）

一、什么是 Laplacian 算子？

Laplacian（拉普拉斯算子）是二階微分算子，用于度量函數在某點處的“變化率的變化”，即函數曲率。

在圖像處理中，它能檢測圖像中灰度變化最顯著的地方——邊緣，尤其是亮度快速變化的區域，對噪聲也很敏感。

數學定義如下：
$\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$

🧮 二、從一維差分到二維卷積核

1. 一維差分

一階差分（梯度近似）：
$\approx f(x+1) - f(x)$
二階差分（Laplacian 近似）：
$\approx f(x+1) + f(x-1) - 2f(x)$
對應的卷積核（差分模板）為：
$k = [1, ? 2, 1]$

2. 推導二維 Laplacian 卷積核

對于二維函數 $f (x, y)$ ：

水平方向二階導數：
$\frac{\partial^2 f}{\partial x^2} \approx f(x+1, y) + f(x-1, y) - 2f(x, y)$
垂直方向二階導數：
$\frac{\partial^2 f}{\partial y^2} \approx f(x, y+1) + f(x, y-1) - 2f(x, y)$
將它們相加：
$\Delta f(x, y) \approx f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x, y)$
這就是最常見的 4 鄰域 Laplacian 模板：
$\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}$

3. 加上對角（斜對角）項：8 鄰域

如果你想讓算子對角方向也敏感，可以擴展為：
$\begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}$

這種核能更廣泛捕捉到不同方向的邊緣，但也更敏感。

OpenCV 使用方式：

cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

參數	含義
`src`	輸入圖像，必須是灰度圖
`ddepth`	輸出圖像的深度，常用 `cv2.CV_64F`，避免溢出
`ksize`	卷積核大小，必須是奇數，一般設為 1 表示使用標準核（上面那個）
`scale`	縮放梯度值，默認 1
`delta`	可選的偏移值，默認 0
`borderType`	邊緣填充方式，默認 `cv2.BORDER_DEFAULT`

與 Sobel 不同，Laplacian 不區分方向，輸出的是一種方向無關的邊緣響應。

示例代碼

# Laplacian算子
import cv2 as cvshudu = cv.imread('../images/shudu.png', cv.IMREAD_GRAYSCALE)# Laplacian算子
dst = cv.Laplacian(shudu, -1, ksize=1)
cv.imshow('shudu', shudu)
cv.imshow('dst', dst)
cv.waitKey(0)
cv.destroyAllWindows()


灰度圖	Laplacian算子

二、圖像邊緣檢測

2.1. 什么是圖像邊緣？

從數學角度來看，圖像邊緣是圖像灰度函數的一階導數（梯度）取得極大值的位置，或二階導數（Laplacian）為零的地方。

我們把二維圖像 $f (x, y)$ 看作一個連續函數，圖像的變化速率（即灰度變化）就是它的梯度：
$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$
梯度的模長即為邊緣強度：
$|\nabla f| = \sqrt{ \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 }$

2. 2. 邊緣檢測的整體流程圖

2. 3. 高斯濾波去噪

邊緣檢測屬于一種“銳化”操作，容易放大噪聲。為此，第一步通常使用高斯濾波對圖像進行平滑處理，消除小范圍內的噪點干擾：

blur = cv2.GaussianBlur(img, (5, 5), 1.4)

高斯核示例（5x5）：
$\frac{1}{273} \begin{bmatrix} 1 & 4 & 7 & 4 & 1\\ 4 & 16 & 26 & 16 & 4\\ 7 & 26 & 41 & 26 & 7\\ 4 & 16 & 26 & 16 & 4\\ 1 & 4 & 7 & 4 & 1 \end{bmatrix}$

2.4. Sobel算子計算梯度與方向

📌 Sobel 卷積核

用于計算圖像在水平與垂直方向上的一階導數：

水平（x方向）：

$G_x = \begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1 \end{bmatrix}$

垂直（y方向）：

$G_y = \begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1 \end{bmatrix}$

梯度值與方向

grad_x = cv2.Sobel(blur, cv2.CV_64F, 1, 0)
grad_y = cv2.Sobel(blur, cv2.CV_64F, 0, 1)
magnitude = cv2.magnitude(grad_x, grad_y)
angle = cv2.phase(grad_x, grad_y, angleInDegrees=True)

梯度幅值（強度）：

$\sqrt{G_x^2 + G_y^2}$

梯度方向：

$\theta = \arctan\left( \frac{G_y}{G_x} \right)$

2.5. 非極大值抑制（NMS）

目的：只保留梯度方向上的局部極大值點，細化邊緣線條。

步驟如下：

對于每一個像素，查找其在梯度方向上的鄰接像素。
如果當前像素的梯度值不是三者中最大的，就將其抑制為0。

為了比較非整數方向上的像素值，需要使用線性插值。

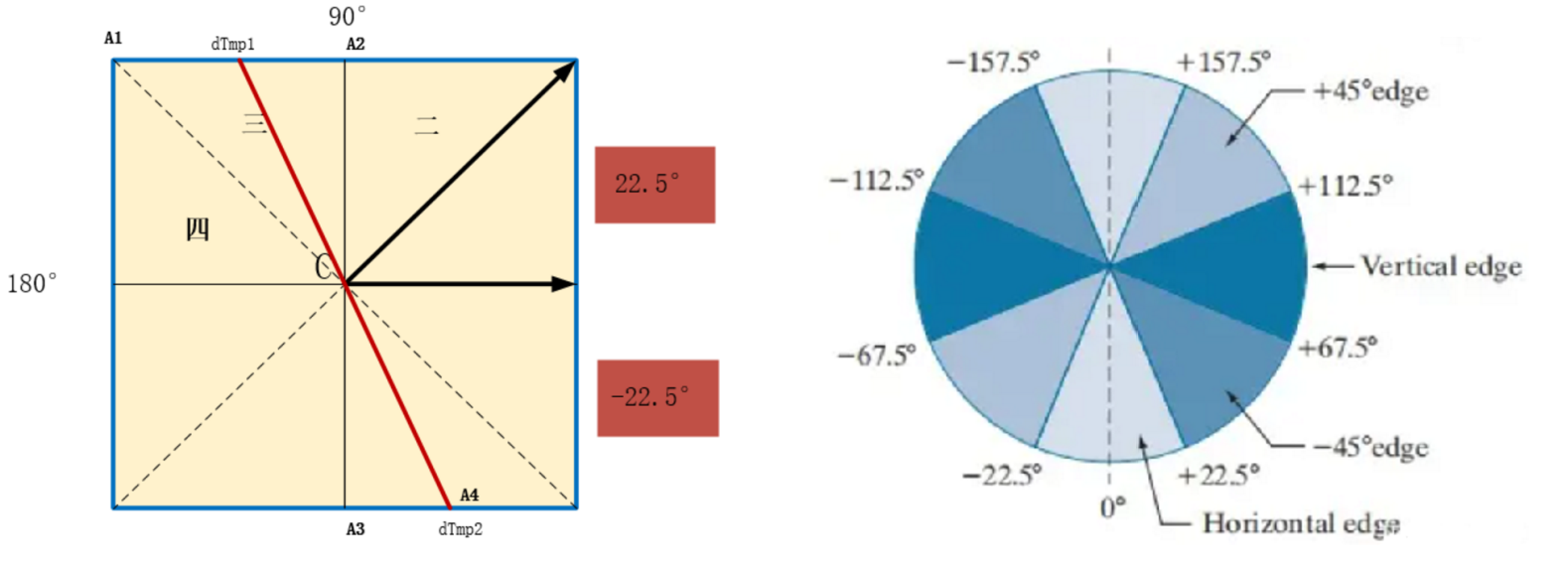
得到 $θ\theta$ 的值之后，就可以對邊緣方向進行分類，為了簡化計算過程,一般將其歸為四個方向：水平方向、垂直方向、45°方向、135°方向。并且：

當 $θ\theta$ 值為-22.5°~22.5°，或-157.5°~157.5°，則認為邊緣為水平邊緣；

當法線方向為22.5°~67.5°，或-112.5°~-157.5°，則認為邊緣為45°邊緣；

當法線方向為67.5°~112.5°，或-67.5°~-112.5°，則認為邊緣為垂直邊緣；

當法線方向為112.5°~157.5°，或-22.5°~-67.5°，則認為邊緣為135°邊緣；

2.6. 雙閾值連接（Hysteresis）

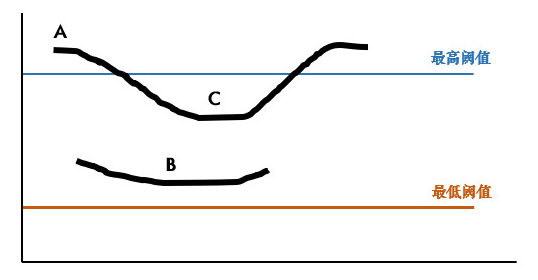
非極大值抑制后，圖像中仍有很多邊緣片段。通過設定高低兩個閾值，連接可靠的邊緣：

高于高閾值 → 強邊緣（保留）
低于低閾值 → 弱邊緣（舍棄）
介于之間 → 如果與強邊緣連接，則保留；否則丟棄

推薦設置

edges = cv2.Canny(img, threshold1=50, threshold2=150)

閾值比建議控制在 2:1 到 3:1 之間。

2.7. Canny 算子：全流程封裝

OpenCV 內置的 Canny 算子封裝了所有步驟：

edges = cv2.Canny(image, 50, 150)

參數說明：

image: 輸入灰度/二值化圖像
threshold1: 低閾值，用于決定可能的邊緣點。
threshold2: 高閾值，用于決定強邊緣點。

2.8. 總結

步驟	作用	工具/算子
高斯濾波	平滑圖像，去除噪聲	`cv2.GaussianBlur`
梯度計算	提取邊緣強度與方向	`cv2.Sobel`
非極大值抑制	邊緣細化	自定義插值
雙閾值鏈接	連接可靠邊緣，抑制偽邊緣	`cv2.Canny`

三、圖像輪廓提取與繪制

圖像輪廓是計算機視覺中一個非常關鍵的概念，它廣泛應用于目標檢測、圖像分割、形狀分析等領域。

3.1 什么是輪廓（Contours）

輪廓是將具有相同灰度值的像素點連接成線的過程。在圖像中，輪廓通常用于表示物體的邊界或形狀。

? 輪廓與邊緣的區別：

邊緣是強度變化的位置（如 Canny）
輪廓是封閉的路徑，更強調形狀和結構
邊緣可能是離散點，輪廓是連續曲線

示意圖：

3.2 尋找輪廓的流程

輪廓提取的流程通常如下：

graph TD
A[彩色圖像] --> B[灰度化]
B --> C[二值化]
C --> D[查找輪廓 \n cv2.findContours（）]

3.3 OpenCV 提供了非常方便的函數：

contours, hierarchy = cv2.findContours(image, mode, method)

3.3.1 參數說明：

參數	說明
`image`	輸入圖像，必須是二值圖像
`mode`	輪廓檢索模式（如下表）
`method`	輪廓逼近方法（如下表）
`contours`	返回的輪廓點坐標數組列表
`hierarchy`	返回輪廓間的層級結構

3.3.2 mode 參數解釋（輪廓層次結構）

mode 值	含義
`RETR_EXTERNAL`	只提取最外層輪廓（最常用）
`RETR_LIST`	提取所有輪廓，但不構建父子關系
`RETR_CCOMP`	提取所有輪廓，并將外層和內層分層保存
`RETR_TREE`	提取所有輪廓并構建完整層次樹結構

層次結構說明圖（RETR_TREE）：

hierarchy[i] = [next, previous, child, parent]

3.3.3 method 參數解釋（輪廓點存儲方式）

method 值	含義
`CHAIN_APPROX_NONE`	保存所有邊界點
`CHAIN_APPROX_SIMPLE`	壓縮冗余點，只保留關鍵點（如直線只保留端點）
`CHAIN_APPROX_TC89_L1`	使用 Teh-Chin 鏈碼逼近算法，效率更高（較少使用）

3.4 繪制輪廓

查找到輪廓后，可以使用以下函數將輪廓畫出來：

cv2.drawContours(image, contours, contourIdx, color, thickness)

參數說明：

參數名	含義
`image`	輸入/輸出圖像（會被修改）
`contours`	找到的輪廓點數組
`contourIdx`	要繪制的輪廓索引（-1 表示繪制所有）
`color`	輪廓線顏色（BGR）
`thickness`	線條粗細，負值表示填充區域

3.5 實戰代碼示例：

import cv2 as cv
from socks import PRINTABLE_PROXY_TYPES# 讀取圖像
img = cv.imread('../images/num.png')# 轉換為灰度圖像
img_gray =cv.cvtColor(img,cv.COLOR_BGR2GRAY)#二值化
_,img_binary = cv.threshold(img_gray,127,255,cv.THRESH_BINARY_INV)# 尋找輪廓
counters,hierarchy = cv.findContours(img_binary,cv.RETR_EXTERNAL,cv.CHAIN_APPROX_SIMPLE)print(counters)
print(len(counters))
print('-------')
print(hierarchy)# 繪制輪廓
cv.drawContours(img,counters,-1,(0,255,0),3,cv.LINE_AA)
cv.imshow('img',img)
cv.waitKey(0)
cv.destroyAllWindows()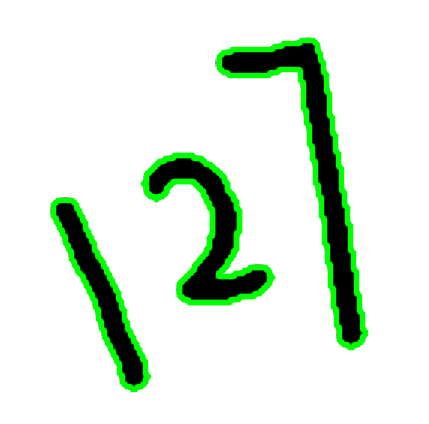

3.6 小貼士：輪廓查找注意事項

🔸 輸入圖像必須為二值圖像（黑白），推薦使用 cv2.threshold()。
🔸 可以先做邊緣檢測（如 Canny），再輪廓提取。
🔸 cv2.findContours() 會修改原圖像，最好用拷貝版本。
🔸 drawContours() 可以搭配 boundingRect()、minAreaRect() 等函數做目標框選。

3.7總結

步驟	內容
1??	灰度化原圖
2??	二值化處理
3??	使用 `cv2.findContours` 提取輪廓
4??	使用 `cv2.drawContours` 繪制輪廓
5??	可結合形狀分析、ROI 提取等進一步處理

四、繪制凸包

我們已經知道了如何獲取輪廓點（contours）以及如何通過 cv2.convexHull() 得到 凸包點集。接下來，我們通過繪圖的方式將凸包顯示出來。

4.1 算法特點

在計算幾何中，**窮舉法（Brute Force）和 QuickHull是兩種常見的凸包（Convex Hull）**構造算法，它們各有優缺點，適用于不同場景。下面為你簡要整理兩者特點，并通過表格進行對比：

1. 窮舉法（Brute Force）

原理：
遍歷所有點對，判斷這條邊是否是凸包邊：即判斷所有其他點是否都在該邊的同一側。若是，則保留該邊。

特點：

算法思想簡單直觀；
時間復雜度較高： $O(n^3)$ ；
適合教學/小規模數據集；
實現容易理解，但不適合大數據場景。

2. QuickHull 算法

原理：
類似快速排序的分治思想。先找出最左和最右的兩個點作為“線段”，劃分上下兩部分遞歸尋找最外層點，逐步構造出凸包。

特點：

平均性能優良，時間復雜度大約為 $\log n)$ ；
適合中大型數據；
實現相對復雜，但效率更高；
對輸入數據分布較敏感（最壞 $O(n^2)$ ）。

函數一覽

函數	功能
`cv2.findContours()`	獲取輪廓點
`cv2.convexHull()`	根據輪廓點獲取凸包點
`cv2.polylines()`	根據點集繪制折線（或閉合多邊形）

# 獲取凸包點
import cv2 as cv# 讀取圖像
image_tu = cv.imread('../images/tu.png')# 轉換為灰度圖像
image_gray = cv.cvtColor(image_tu, cv.COLOR_BGR2GRAY)# 二值化處理
_,image_binary = cv.threshold(image_gray,127,255,cv.THRESH_BINARY)# 尋找輪廓
counters,_ = cv.findContours(image_binary,cv.RETR_EXTERNAL,cv.CHAIN_APPROX_SIMPLE)# 獲取凸包
convex_hull= []
for cnt in counters:convex_hull.append(cv.convexHull(cnt))cv.polylines(image_tu,convex_hull,True,(255,0,0),3,cv.LINE_AA)
cv.imshow('binary',image_binary)
cv.imshow('tu',image_tu)
cv.waitKey(0)
cv.destroyAllWindows()

4.4 結果效果

假設你的原始圖像中有一個不規則物體，該代碼會：

提取其輪廓
計算包住這個物體的最小凸多邊形（凸包）
用線條將這個凸包標出

如圖所示：

4.5 應用場景總結

應用領域	使用場景
手勢識別	識別手指個數：凸包與缺陷分析（defects）
目標檢測	將不規則輪廓轉為規則包圍多邊形
圖像壓縮	簡化輪廓特征
安全區域	包圍任意散點區域