一、什么是函數遞歸

函數遞歸是一種解決問題的思想，是將一個大的問題化為一個一個小的問題（類似于剝洋蔥），是在一個函數體內部自己調用自己的方法。遞歸就是遞推加回歸，是基于函數實現的。
例如：

// 第一個最簡單的函數遞歸程序：int main()
{printf("hahaha\n");main();       // 在main函數體內再次調用自己，這就是遞歸return 0;
}

運行結果：

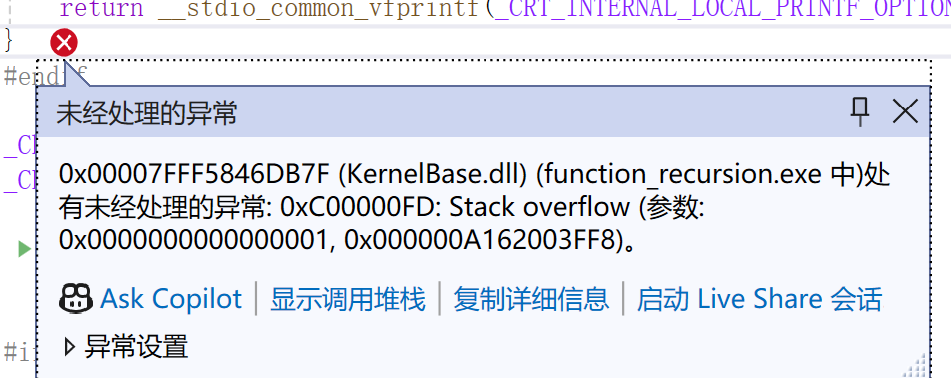
但是這是一個問題程序，因為沒有臨界條件，所以會死遞歸下去，最終導致出現上圖中棧溢出（Stack overflow）。
因為每一次函數遞歸都會創建函數棧幀，此棧幀創建在內存的棧區，最終死遞歸，棧區空間消耗完畢，出現棧溢出的問題。

二、函數遞歸的要點

基于點一，函數遞歸有以下兩個要點：

1. 函數遞歸要有臨界條件，每次遞歸后都要逼近此條件，否則會出現死遞歸的情況，到達臨界條件，將不再函數調用
2. 并不是所有的程序都能寫成函數遞歸形式，并且就算是能寫成函數遞歸的形式，在函數遞歸調用過程中會創建函數棧幀，產生運行時的開銷（空間，時間），空間可能出現棧溢出的問題，時間影響運行效率，所以在某些程序中迭代（循環）和遞歸形式都能實現，并且遞歸實現代碼比迭代實現更加復雜，那么還是使用迭代實現。

三、示例

1.計算n的階乘

實現思路：

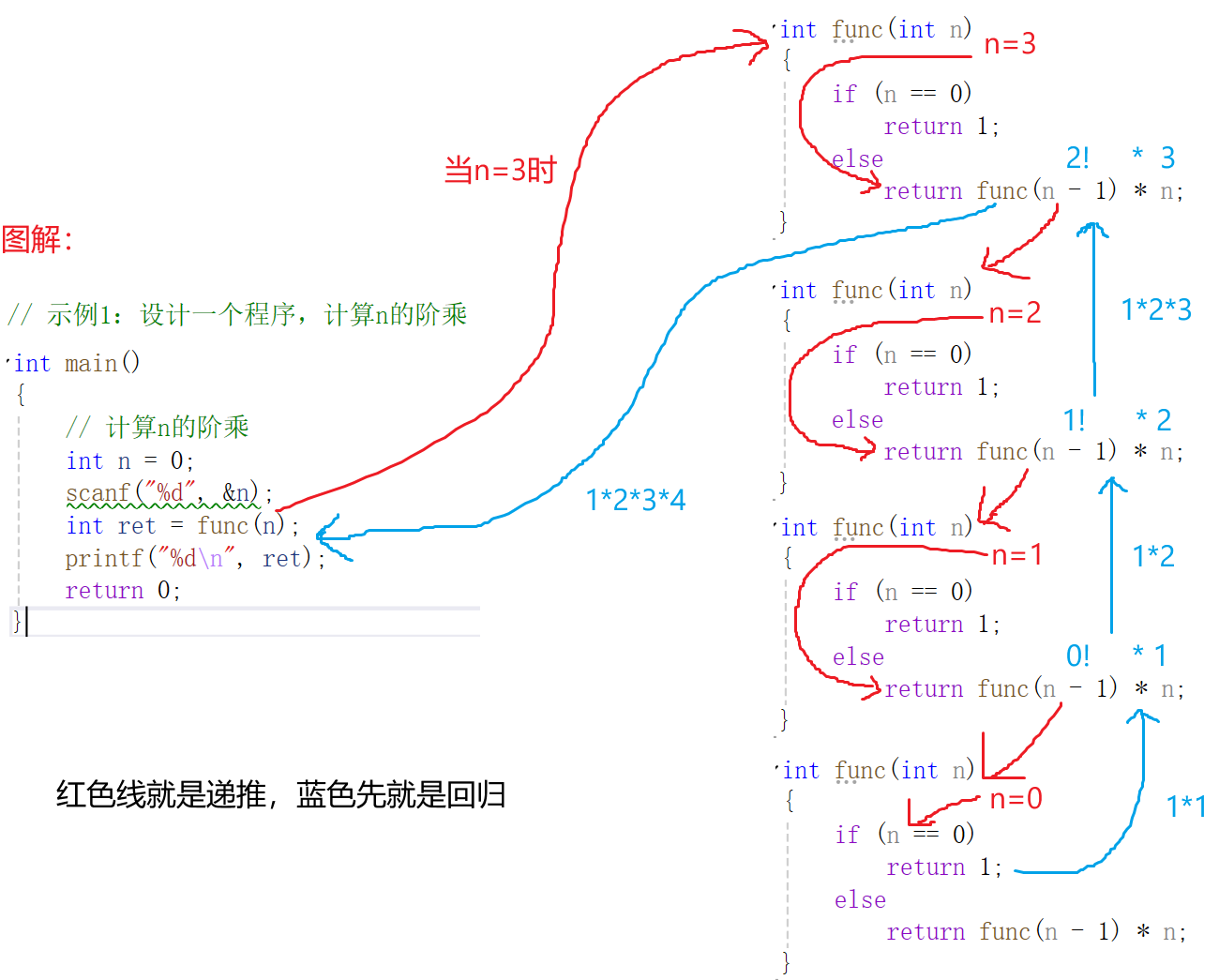
// 示例1：設計一個程序，計算n的階乘
int func(int n)
{if (n == 0)return 1;elsereturn func(n - 1) * n;
}int main()
{// 計算n的階乘int n = 0;scanf("%d", &n);int ret = func(n);printf("%d\n", ret);return 0;
}

遞歸過程：

2.提取一個任意正整數的所有位數，按順序排列

實現思路：

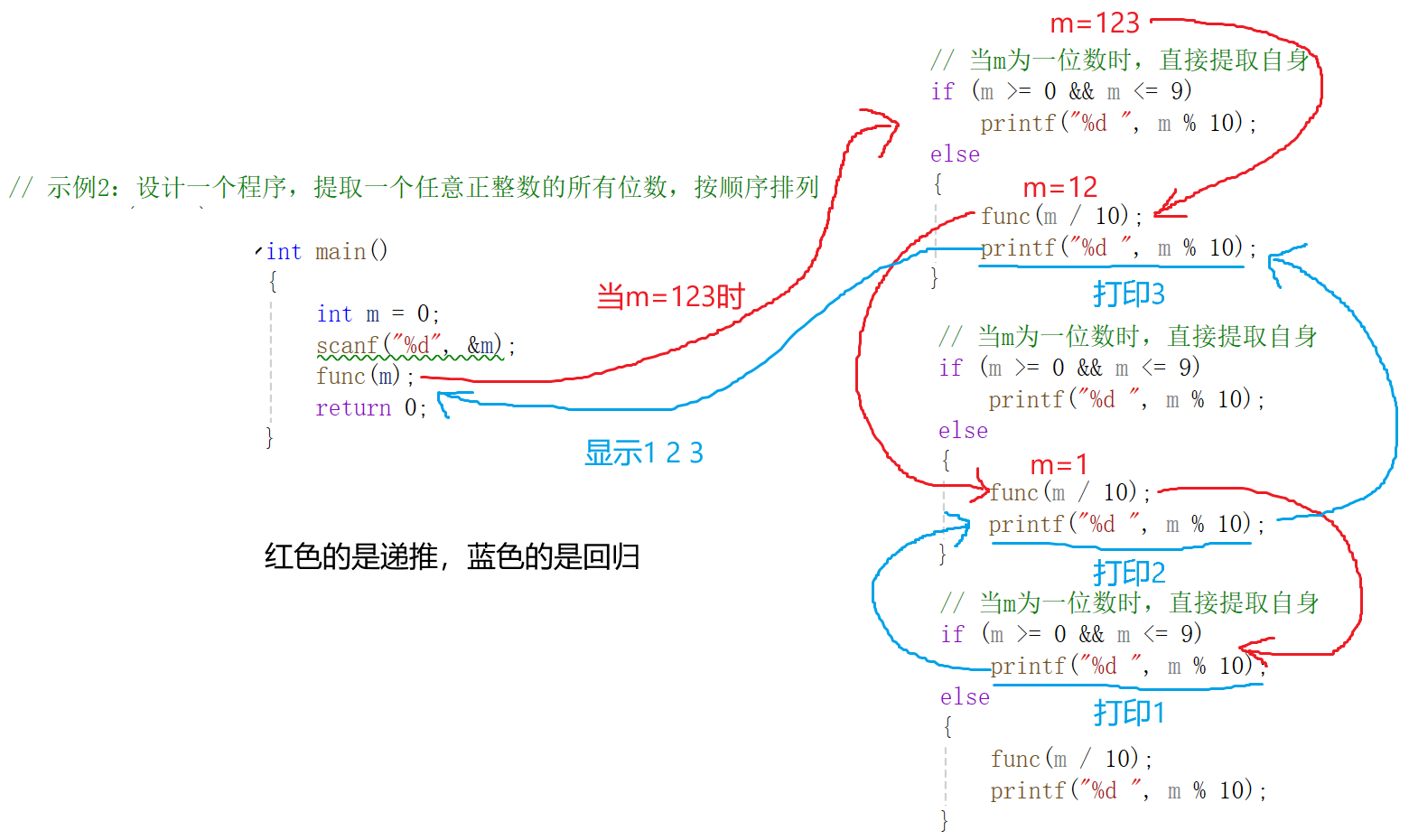
// 示例2：設計一個程序，提取一個任意正整數的所有位數，按順序排列
void func(int m)
{// 當m為一位數時，直接提取自身if (m >= 0 && m <= 9)printf("%d ", m % 10);else{func(m / 10);printf("%d ", m % 10);}
}int main()
{int m = 0;scanf("%d", &m);func(m);return 0;
}

遞歸過程：

3.獲取第n個斐波那契數，最開始的兩個數是1，1

實現思路：

// 示例3：設計一個程序，獲取第n個斐波那契數，最開始的兩個數是1，1
int fib(int n)
{if (n == 1 || n == 2){return 1;}else{return fib(n - 1) + fib(n - 2);}
}int main()
{int n = 0;scanf("%d", &n);int ret = fib(n);printf("%d\n", ret);return 0;
}

這里直接說出結果，這是一個有問題的遞歸程序，當n很大很大的時候，上述代碼執行效率非常低下，因為：

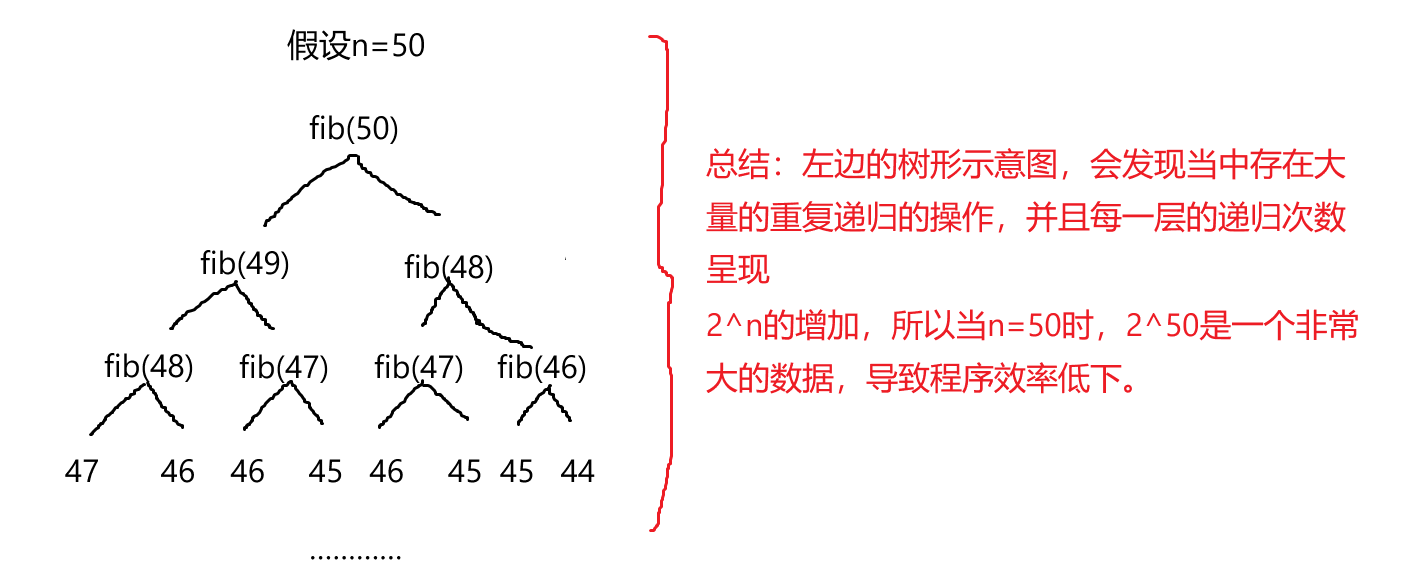
所以這就是一個邏輯思維上運用遞歸的思想，但是遞歸實現出來有些許問題，正確的思路：
定文三個變量，a，b，c，讓a等于0位置上的數據，b等于1位置上的數據，c等中于a加上b的數據，c就是我們所求的第n個斐波那契數。之后再先讓b的值賦值給給a，c的值賦值給給b，循環下去，直到n>2才結束。最后返回c。

int fib(int n) {// 定義三個變量，a，b，c// a是第一個數字1，b是第二個數字1// c是我們所需要的第n個斐波那契數int a=1, b=1,c;// 當所求斐波那契數是前兩個的時候，直接給定值即可if(n == 1 && n == 2)c=a;      // 此時斐波那契數就是1// 當所求斐波那契數是從第三個開始時while(n > 2){c = a + b;// 更新數據，注意別出現數據覆蓋的情況a = b;b = c;n--; }// 返回斐波那契數return c;}

四、總結

上述的遞歸演示，第一個main函數內部再次調用自己導致出現棧溢出的錯誤是因為沒有設定臨界條件；前兩個示例演示了如何分析一個程序如何變成遞歸思想，并且理清它的遞歸調用關系；最后一個示例就演示了在某寫可以寫成遞歸的程序，但是遞歸的實現有問題的這種程序，建議是使用迭代的思想去實現。