NeRF

NeRF資源

計算機視覺的問題

計算機視覺終極問題定義為：輸入二維圖像，輸出是由二維圖像"重建"出來的三維物體的位置與形狀

NeRF

定義

環境：靜態場景表示為一個連續的 5D 函數
輸出：輸出空間中每個點 (x, y, z) 在各個方向 (θ, φ) 上的輻射度，以及每個點的密度
方法：優化了一個沒有任何卷積層的深度全連接神經網絡（通常稱為多層感知機或 MLP），通過從單個 5D 坐標 (x, y, z, θ, φ) 回歸到單個體積密度和與視圖相關的 RGB 顏色來表示這個函數
步驟：
1）讓相機光線穿過場景以生成一組采樣的 3D 點
2）使用這些點及其對應的 2D 觀看方向作為神經網絡的輸入，以生成一組輸出顏色和密度(這組顏色和密度對應采樣的3D點)
3）使用經典的體渲染技術將這些顏色和密度累積成 2D 圖像
優化模型：使用梯度下降來優化這個模型，同時最小化每個觀察到的圖像與從我們的表示中渲染的相應視圖之間的誤差。跨多個視圖最小化這種誤差會促使網絡通過為包含真實底層場景內容的位置分配高體積密度和準確顏色來預測場景的連貫模型。

神經輻射場場景表示

場景函數：連續場景表示為一個 5D 向量值函數
函數輸入：** 3D 位置 x=(x,y,z) 和 2D 觀看方向d (θ,?)**
函數輸出：發射顏色 c=(r,g,b) 和體積密度 σ
全連接多層卷積深度神經網絡：MLP 網絡 FΘ?:(x,d)→(c,σ) 近似這個連續的 5D 場景表示，并優化其權重 Θ
目標：每個輸入的 5D 坐標映射到對應的體積密度σ和方向發射顏色c
預測函數：體積密度 σ 預測為位置 x 的函數 | RGB 顏色 c 作為位置x和觀看方向d的函數
網絡實現：(多階段)
1. MLP FΘ?第一階段使用8 個全連接層(采用 ReLU 激活函數，每層 256 個通道)處理輸入的 3D 坐標 x，輸出輸出 σ 和一個 256 維的特征向量
2. 第二階段：該特征向量與相機光線的觀看方向連接并傳遞到一個**額外的全連接層（采用 ReLU 激活函數，128 個通道）**該層輸出與視圖相關的 RGB 顏色
(下圖展示：場景分別在海面以及船面是連續場可微分的——>平滑過渡)

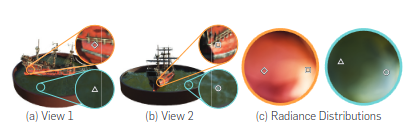
基于輻射場的體渲染

利用體渲染技術從神經輻射場中合成圖像——體渲染通過數值積分將 3D 體積密度和發射顏色投影到 2D 圖像平面

下圖解釋了：沿光線采樣點信息r(t)，針對于每個采樣點利用積分得到該點的累積顏色。

對于公式的理解：

1. 體積密度 σ(r(t))：表示光線在點 r(t) 處被吸收或散射的概率密度——σ 越大，光線越容易在此處 “終止”
2. 發射顏色 c(r(t),d)：表示點 r(t) 在觀察方向 d 上發射的顏色——物體表面的反射光 | 介質自身的發光
3. 透射率 T(t)：表示光線從起點 tn? 傳播到 t 時未被吸收的概率
   如果沿途密度 σ 越高，透射率 T(t) 越低（光線被吸收的概率越大）
   
   所以最終的體積渲染公式得到的沿著整條光線累積的顏色可以理解為：其發射顏色與未被前方物體著當的概率加權
   將積分離散化為沿每條光線的有限和。我們在 [tn?,tf?] 范圍內均勻采樣 N 個點 t1?<t2?<?<tN?，并使用以下黎曼和近似：
   

分層采樣

針對于每條光線執行粗采樣和細采樣的分層采樣
粗網絡：首先在 [tn?,tf?] 范圍內均勻采樣 Nc? 個點，使用方程 (2) 計算粗渲染結果 C_c??
細網絡：在密度較高的區域（如表面附近）自適應地添加更多采樣點 N_f?
最終使用這些點重新計算細渲染結果 C_f??,更精確地表示場景中的高頻細節
(通過自適應的增加更多的采樣點——具體通過定義一個PDF概率密度函數)，并基于這個PDF函數增加額外的采樣點：
如何通過PDF函數實現重要性采樣

標準的均勻采樣造成資源的浪費
在低密度區域（如空曠空間），采樣點對最終顏色貢獻極小。
在高密度區域（如物體表面），少量采樣點可能無法準確捕捉顏色變化。
分層采樣的目標是：在保持總采樣點數不變的情況下，自適應地將更多采樣點分配到對最終結果貢獻更大的區域（即高概率區域）



這里需要注意CDF函數是計算到當前位置的累加權重，通過均勻分布產生的隨機數代表權重，對每個隨機數找到對應的區間，然后用線性插值的方法，將這個隨機數插值到對應的區間

最終插值得到新點的位置

優化神經輻射場

支持對高分辨率復雜場景的表示——第一項是輸入坐標的位置編碼|它幫助多層感知機表示高頻函數|第二項是分層采樣過程
在將輸入傳遞給網絡之前，使用高頻函數將輸入映射到更高維空間，能夠更好地擬合包含高頻變化的數據
三角化基礎點

位置編碼——高維信息
并證明將 FΘ? 重新構造為兩個函數的組合 FΘ?=FΘ′?°γ（一個是學習的，另一個不是）
γ 是從 R 到更高維空間 R^2L 的映射，而 FΘ′? 仍然只是一個常規的 MLP。形式上，我們使用的編碼函數為：
γ§=(sin(20πp),cos(20πp),?,sin(2L?1πp),cos(2L?1πp))
γ(*)函數分別應用于 x 中的三個坐標值和笛卡爾觀察方向單位向量 d 的三個分量

優化實現細節：每個場景優化一個單獨的神經連續體表示網絡。
輸入：捕獲 RGB 圖像數據集、相應的相機位姿和內參，以及場景邊界
優化過程：每個優化迭代中，我們從數據集中的所有像素中隨機采樣一批相機光線。我們沿著每條光線在 N 個隨機點查詢網絡，使用體渲染過程，利用這些樣本渲染每條光線的顏色。損失只是渲染像素顏色與真實像素顏色之間的總平方誤差：

基礎知識

初始化

選擇條件：選擇足夠的重疊區域——確保穩定提取特征點并進行魯棒性匹配
高冗余性：周圍有大量相鄰的圖像可以快速擴展重建網絡

SFM

通過三維場景的多張圖像，恢復出該場景的三維結構信息以及每張圖像對應的攝像機參數
坐標系與相機參數：
從像平面到像素平面的單位變化是“從m到像素為單位

歐式結構恢復問題定義：

第一個相機坐標系與世界坐標系重疊：

通過八點法估計基礎矩陣，然后通過基礎矩陣估計本質矩陣存在的問題(尺度、符號不能確定)

對于W矩陣和Z矩陣的定義：

對于R旋轉矩陣的計算：

E的因式分解只是保證了矩陣分解為正交的，如果保證為旋轉矩陣，需要保證行列式的值為正

真實的解：知道第一個和第二個攝像機的投影矩陣以及對應的三維點的坐標X，那么進行三角化，正確的解保證該點在兩個相機的z坐標均為正。

單個點存在噪聲——>多個點進行三角化，對解進行投票

歐式結構恢復的歧義
恢復結構與真實結構在尺寸，旋轉(真實的結構的朝向)，平移(真實的經緯度)



內參矩陣：最終反映的是以物理尺寸為單位的焦距 f 轉換成像素為單位的焦距值
內參矩陣描述的是：相機坐標系到像素坐標系的變化
外參矩陣描述的是：世界坐標系到相機坐標系之間的轉換關系
相機的內參矩陣以及外參矩陣都是相機的關鍵參數
投影矩陣：世界坐標系到影像坐標系(u,v)之間的轉換關系表達的是透視投影中空間點到像點的投影關系——對應的矩陣稱之為投影矩陣

基礎矩陣 & 本質矩陣 & 單應矩陣

可以建立兩個視圖公共點之間的坐標聯系，或者完成公共點之間的坐標轉換。
===基礎矩陣：對規范化(攝像機的內參矩陣K是單位矩陣的形式)攝像機拍攝的兩個視點間的圖像的幾何關系進行代數描述=
關鍵矩陣
本質矩陣的屬性：

e為極點：
極點肯定在左圖像點p對應的在右圖像的極線上，所以也就有l_q^T e^’ = 0 也就得出Ee = 0

基礎矩陣：是對一般的透視攝像機(非規范化攝像機)的兩個視點的圖像間的極幾何關系進行描述
思想：對內參矩陣求逆，得到規范化攝像機下的坐標[I,0]


基礎矩陣的性質：

基礎矩陣和本質矩陣的區別：刻畫了更加一般的透視攝像機之間的在不同圖像之間的對應點的極幾何約束關系
只需要基礎矩陣F，無需場景信息以及相機的內外參數，即可簡歷左右圖像對之間的對應關系
F包含了內參信息，以及R和t的信息

本質矩陣描述了：兩個像素坐標系x₁,x₂之間的關系，即空間點在兩個相機的成像點通過外參矩陣R，t建立了一個等式關系，或者稱為一種約束，這個約束就叫做對極約束
對極約束
本質矩陣與基礎矩陣的區別：本質矩陣是和 x建立的關系，而 x是由內參矩陣 K和像素坐標p 計算出來的，所以本質矩陣使用的前提是內參矩陣 K已知；而基礎矩陣直接和像素坐標 p 建立聯系，所以不需要已知內參矩陣。
本質矩陣的性質：一個3×3的矩陣是本質矩陣的充要條件是它的奇異值中有兩個相等而第三個是0

從已經估得的本質矩陣E，恢復出相機的運動R,t

通過SVD分解：

SVD 分解

SVD分解鏈接
定義：SVD是將一個任意矩陣分解為三個矩陣。所以如果我們有一個矩陣A，那么它的SVD可以表示為：
意義：奇異值分解則是特征分解在任意矩陣上的推廣
應用：
PCA主成分分析：把數據集映射到低維空間中去。 數據集的特征值（在SVD中用奇異值表征）按照重要性排列，降維的過程就是舍棄不重要的特征向量的過程，而剩下的特征向量組成的空間即為降維后的重要特征空間。
圖片壓縮：在圖像處理中，SVD分解常被用于圖像壓縮。通過對圖像矩陣進行SVD分解，可以得到較低秩的近似矩陣，從而減少存儲空間和傳輸帶寬。

在SVD中，U和 V 對于任何矩陣都是可逆的，并且它們是正交歸一的，奇異值比特征值在數值上更穩定(奇異值是正特征值的平方根)
理解SVD實現數據降維：