拐點(Inflection Point)詳解:定義、原理與應用
在數學分析與數據建模中,“拐點(Inflection Point)”是一個非常重要的概念。今天這篇文章,我們將結合圖示,深入理解拐點的定義、數學意義、識別方法以及實際應用場景。
什么是拐點?
拐點,英文稱為 Inflection Point,是曲線形狀發生變化的特殊位置。
正式定義:
拐點是函數圖像上由凸函數變成凹函數的點,或者是由凹函數變成凸函數的點。
簡單來說,就是函數的曲率方向發生改變的位置。在拐點處,曲線從“向上彎”變為“向下彎”,或者反之。
圖示說明:
下圖直觀展示了拐點的位置:
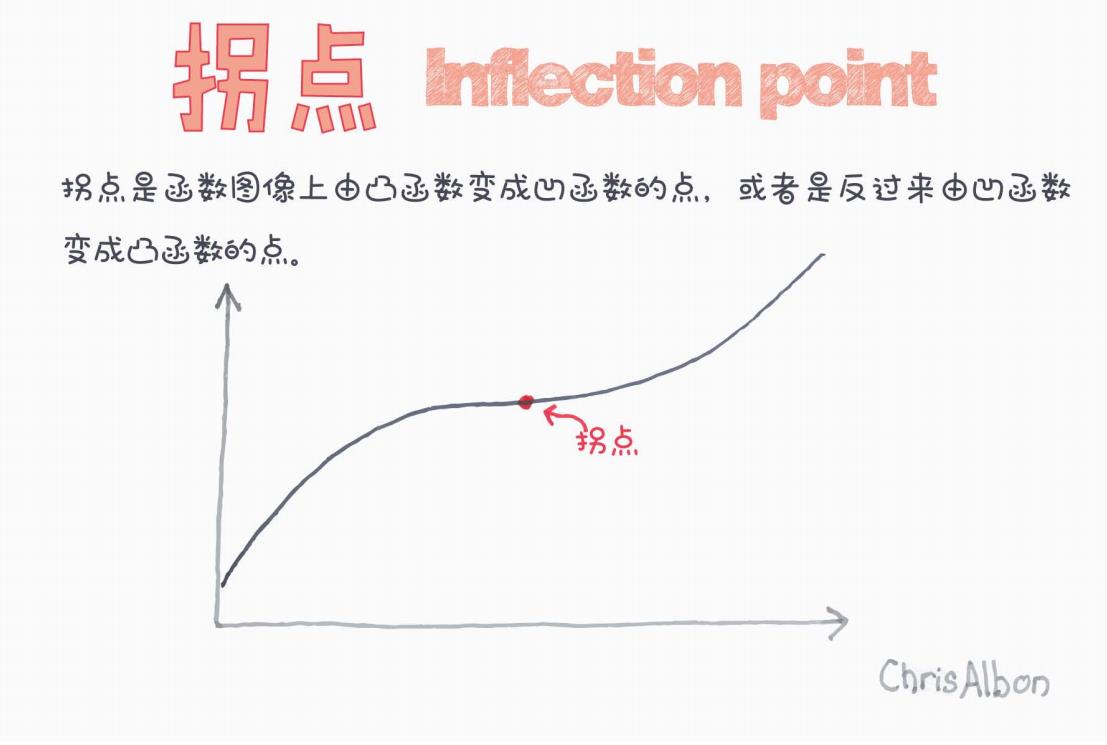
在圖中,可以看到曲線在紅色標記點(拐點)處,發生了由凹變凸的轉變。
數學角度理解拐點
1. 凸性與凹性
在拐點討論中,凸性(convexity)和凹性(concavity)是基礎。
-
如果函數在某區間上開口朝上(像一個笑臉弧線),則稱為凸。
-
如果函數在某區間上開口朝下(像一個皺眉的弧線),則稱為凹。
2. 二階導數與拐點
二階導數 f''(x) 提供了判斷函數曲率的依據:
-
當 f''(x) > 0 時,函數是凸的。
-
當 f''(x) < 0 時,函數是凹的。
-
當 f''(x) = 0 并且符號發生變化時,x?對應的位置就是拐點。
拐點判定步驟:
-
計算函數的二階導數 f''(x)。
-
解方程 f''(x) = 0,找出候選點。
-
檢查這些點在前后左右的二階導數符號是否發生變化。
-
符號變化的點即為拐點。
拐點在實際中的應用
拐點不僅是數學分析中的基礎概念,還在各種實際應用中扮演重要角色,比如:
1. 機器學習與深度學習
在訓練過程中,學習曲線的拐點可能意味著模型開始過擬合,需要采取正則化或早停等措施。
2. 數據分析與趨勢預測
在銷售增長曲線中,拐點可能代表市場飽和點或者增長加速點,有助于企業做出戰略調整。
3. 金融投資
股價曲線的拐點常被用于判斷趨勢反轉,是技術分析中的關鍵節點。
4. 生物統計與醫學研究
疾病傳播曲線的拐點可以用來預測疫情爆發、拐點控制等。
舉例:拐點計算示范
以簡單函數 為例:
-
一階導數:
-
二階導數:
令二階導數為零:
檢查 x=0 左右的二階導數符號變化:
-
當 x < 0,f''(x) < 0(凹)
-
當 x > 0,f''(x) > 0(凸)
所以,x=0 是函數 的拐點。
小結
-
拐點是曲線由凸變凹或由凹變凸的位置。
-
二階導數為判斷拐點提供了有效的工具。
-
拐點分析在機器學習、金融、疫情分析等領域都有重要應用。
掌握拐點的概念不僅能提升數學素養,也能幫助我們更好地理解和應用數據變化背后的規律。
作者注:本文參考了 Chris Albon 的手繪圖進行解釋,圖片風格清新有趣,希望能幫助大家更輕松地理解這一抽象概念。
如果你喜歡這樣的圖文結合講解,歡迎點贊、收藏、關注我!






)





)


)



