注：本文為 “線性代數 · 矩陣 | 秩” 相關合輯。
圖片清晰度受引文原圖所限。
略作重排，未全校去重。
如有內容異常，請看原文。

---

矩陣的秩及其應用

一、矩陣秩的基本概念

（一）k 階子式

設矩陣 $A=(a_{ij}{)}_{m\times n}$，在矩陣 $A$ 中任意選取 $k$ 行（$1\le k\le m$）和 $k$ 列（$1\le k\le n$），將位于這些行與列交叉處的 $k^2$ 個元素按原有的相對位置組成一個 $k$ 階行列式，該行列式稱為矩陣 $A$ 的一個 k 階子式。

對于 $m\times n$ 矩陣 $A$，$k$ 階子式的總數為組合數 ${\mathrm{C}}_m^k\times {\mathrm{C}}_n^k$（其中 ${\mathrm{C}}_n^k=\frac{n!}{k!(n?k)!}$ 表示從 $n$ 個元素中選取 $k$ 個元素的組合數）。

示例：設矩陣 $A=\left(\begin{array}{cccc}1& 2& 3& 4\\ 1& 3& 4& 1\\ 1& 4& 1& 2\end{array}\right)$

• 選取第 1、2 行和第 2、4 列，交叉處元素組成的 2 階子式為 $D_2^{\prime }=\left|\begin{array}{cc}2& 4\\ 3& 1\end{array}\right|$；
• 選取第 1、3 行和第 1、3 列，交叉處元素組成的 2 階子式為 $D_2^{\prime \prime }=\left|\begin{array}{cc}1& 3\\ 1& 1\end{array}\right|$；
• 該矩陣的 2 階子式總數為 ${\mathrm{C}}_3^2\times {\mathrm{C}}_4^2=3\times 6=18$，3 階子式總數為 ${\mathrm{C}}_3^3\times {\mathrm{C}}_4^3=1\times 4=4$。

（二）矩陣秩的定義

設矩陣 $A=(a_{ij}{)}_{m\times n}$，若存在一個 $r$ 階子式不為 $0$，且所有 $r+1$ 階子式（若存在）全為 $0$，則稱 $r$ 為矩陣 $A$ 的秩，記作 $R(A)$ 或 $\mathrm{rank}(A)$。

特殊規定：零矩陣（所有元素均為 $0$ 的矩陣）的秩為 $0$，即 $R(0)=0$。

重要結論：

1. 對任意 $m\times n$ 矩陣 $A$，必有 0≤R(A)≤min?{m,n}0 \leq R(A) \leq \min\{m, n\}0≤R(A)≤min{m,n}；
2. 若 $n$ 階方陣 $A$ 的秩 $R(A)=n$，則稱 $A$ 為 滿秩矩陣（或非奇異矩陣），此時 $\det (A)\ne 0$（$\det (A)$ 表示矩陣 $A$ 的行列式）；
3. 若 $n$ 階方陣 $A$ 的秩 $R(A)<n$，則稱 $A$ 為 降秩矩陣（或奇異矩陣），此時 $\det (A)=0$。

（三）秩的等價描述

矩陣的秩本質反映了矩陣中行（或列）向量的線性無關性，具體等價描述如下：

• 行秩：矩陣 $A$ 的行向量組中線性無關的行向量的最大個數；
• 列秩：矩陣 $A$ 的列向量組中線性無關的列向量的最大個數；
• 定理：對任意矩陣 $A$，其行秩 = 列秩 = 秩（即 $R(A)=\text{行秩}=\text{列秩}$）。

二、矩陣秩的計算方法

（一）子式判別法（定義法）

根據矩陣秩的定義，通過尋找“最高階非零子式”來確定秩，步驟如下：

1. 從低階子式開始計算，先判斷 1 階子式（即矩陣元素）是否全為 $0$：若全為 $0$，則 $R(A)=0$；若存在非零 1 階子式，繼續判斷 2 階子式；
2. 若存在非零 2 階子式，繼續判斷 3 階子式，以此類推；
3. 找到最大的 $r$，使得存在非零 $r$ 階子式，且所有 $r+1$ 階子式全為 $0$，則 $R(A)=r$。

示例 1：求矩陣 $A=\left(\begin{array}{cccc}1& 2& 3& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 0\end{array}\right)$ 的秩

• 選取第 1、2、3 行和第 1、2、3 列，組成的 3 階子式為 $\left|\begin{array}{ccc}1& 2& 3\\ 0& 1& 0\\ 0& 0& 1\end{array}\right|=1\ne 0$；
• 矩陣 $A$ 為 $3\times 4$ 矩陣，不存在 4 階子式；
• 因此 $R(A)=3$。

示例 2：求矩陣 $D=\left(\begin{array}{ccc}1& 2& 5\\ 0& 3& 4\\ 0& 0& 0\end{array}\right)$ 的秩

• 1 階子式（如元素 $1$、$2$、$5$ 等）非零，2 階子式（如 $\left|\begin{array}{cc}1& 2\\ 0& 3\end{array}\right|=3\ne 0$）非零；
• 所有 3 階子式（僅 1 個，即矩陣 $D$ 的行列式）為 $\left|\begin{array}{ccc}1& 2& 5\\ 0& 3& 4\\ 0& 0& 0\end{array}\right|=0$；
• 因此 $R(D)=2$（原內容此處寫為 $R(A)$，屬于符號混淆，已修正為 $R(D)$）。

（二）初等變換法（最常用方法）

1. 重要定理

矩陣的初等變換（行變換或列變換）不改變矩陣的秩，即若矩陣 $A$ 經過初等變換化為矩陣 $B$，則 $R(A)=R(B)$。

初等變換的類型：

• 行變換：
  1. 交換兩行（記為 $r_i?r_j$）；
  2. 用非零常數 $k$ 乘某一行（記為 $k{r}_i$，$k\ne 0$）；
  3. 某一行的 $k$ 倍加到另一行（記為 $r_i+k{r}_j$）。
• 列變換：
  1. 交換兩列（記為 $c_i?c_j$）；
  2. 用非零常數 $k$ 乘某一列（記為 $k{c}_i$，$k\ne 0$）；
  3. 某一列的 $k$ 倍加到另一列（記為 $c_i+k{c}_j$）。

2. 行階梯形矩陣的定義

滿足以下兩個條件的矩陣稱為 行階梯形矩陣：

1. 全零行（所有元素均為 $0$ 的行）位于矩陣的下方；
2. 非零行的第一個非零元素（稱為“主元”）的列序數，從上到下嚴格遞增。

示例：$\left(\begin{array}{cccc}1& 0& 2& ?4\\ 0& 1& ?1& 2\\ 0& 0& 0& 0\end{array}\right)$ 是行階梯形矩陣（主元分別在第 1 列、第 2 列，列序數遞增，全零行在最下方）。

3. 計算步驟

1. 對矩陣 $A$ 施行初等行變換，將其化為行階梯形矩陣 $B$；
2. 行階梯形矩陣 $B$ 中非零行的行數，即為矩陣 $A$ 的秩（$R(A)=\text{非零行數}$）。

示例 1：求矩陣 $A=\left(\begin{array}{cccc}1& 0& 2& ?4\\ 2& 1& 3& ?6\\ ?1& ?1& ?1& 2\end{array}\right)$ 的秩

• 第一步：消去第 1 列下方元素（以第 1 行第 1 列元素 $1$ 為主元）
  $A\stackrel{r_2?2r_1}{\to }\left(\begin{array}{cccc}1& 0& 2& ?4\\ 0& 1& ?1& 2\\ ?1& ?1& ?1& 2\end{array}\right)\stackrel{r_3+r_1}{\to }\left(\begin{array}{cccc}1& 0& 2& ?4\\ 0& 1& ?1& 2\\ 0& ?1& 1& ?2\end{array}\right)$；
• 第二步：消去第 2 列下方元素（以第 2 行第 2 列元素 $1$ 為主元）
  $\stackrel{r_3+r_2}{\to }\left(\begin{array}{cccc}1& 0& 2& ?4\\ 0& 1& ?1& 2\\ 0& 0& 0& 0\end{array}\right)$；
• 行階梯形矩陣中非零行的行數為 $2$，因此 $R(A)=2$。

示例 2：求矩陣 $A=\left(\begin{array}{ccc}4& ?2& 1\\ 1& 2& ?2\\ ?1& 8& ?7\\ 2& 14& ?13\end{array}\right)$ 的秩

• 第一步：交換第 1、2 行（使第 1 列主元為 $1$，簡化計算）
  $A\stackrel{r_1?r_2}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 4& ?2& 1\\ ?1& 8& ?7\\ 2& 14& ?13\end{array}\right)$；
• 第二步：消去第 1 列下方元素
  $\stackrel{r_2?4r_1}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 0& ?10& 9\\ ?1& 8& ?7\\ 2& 14& ?13\end{array}\right)\stackrel{r_3+r_1}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 0& ?10& 9\\ 0& 10& ?9\\ 2& 14& ?13\end{array}\right)\stackrel{r_4?2r_1}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 0& ?10& 9\\ 0& 10& ?9\\ 0& 10& ?9\end{array}\right)$；
• 第三步：消去第 2 列下方元素
  $\stackrel{r_3+r_2}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 0& ?10& 9\\ 0& 0& 0\\ 0& 10& ?9\end{array}\right)\stackrel{r_4+r_2}{\to }\left(\begin{array}{ccc}1& 2& ?2\\ 0& ?10& 9\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$；
• 行階梯形矩陣中非零行的行數為 $2$，因此 $R(A)=2$。

（三）含參數矩陣的秩（需分類討論）

當矩陣中含參數時，需根據參數的取值判斷最高階非零子式的階數，進而確定秩。

示例：設矩陣 $A=\left(\begin{array}{cccc}1& ?1& 1& 2\\ 3& \lambda & ?1& 2\\ 5& 3& \mu & 6\end{array}\right)$，且 $R(A)=2$，求 $\lambda$ 和 $\mu$ 的值

• 第一步：對 $A$ 施行初等行變換化為行階梯形
  $A\stackrel{r_2?3r_1}{\to }\left(\begin{array}{cccc}1& ?1& 1& 2\\ 0& \lambda +3& ?4& ?4\\ 5& 3& \mu & 6\end{array}\right)\stackrel{r_3?5r_1}{\to }\left(\begin{array}{cccc}1& ?1& 1& 2\\ 0& \lambda +3& ?4& ?4\\ 0& 8& \mu ?5& ?4\end{array}\right)$；
• 第二步：由 $R(A)=2$ 可知，行階梯形矩陣中第 3 行需為全零行，因此第 2、3 行對應元素成比例
  即 $\frac{\lambda +3}{8}=\frac{?4}{\mu ?5}=\frac{?4}{?4}$；
• 第三步：求解比例方程
  由 $\frac{?4}{?4}=1$，得 $\lambda +3=8\times 1?\lambda =5$；$?4=(\mu ?5)\times 1?\mu =1$；
• 因此，當 $\lambda =5$ 且 $\mu =1$ 時，$R(A)=2$。

三、矩陣化簡的形式與方法

（一）矩陣化簡的基本原理

矩陣化簡通過初等變換（行變換或列變換）實現，初等變換不改變矩陣的秩，是計算秩、求解線性方程組的關鍵工具。常見化簡目標包括行階梯形、行簡化行階梯形、列階梯形及等價標準形，不同形式適用于不同場景。

（二）常見化簡形式及規則

1. 行階梯形（Row Echelon Form, REF）

REF 是“階梯狀”的基礎化簡形式，需滿足以下 4 條規則：

1. 全零行位于矩陣最下方；
2. 非零行的第一個非零元素（稱為“主元”）的列索引，嚴格大于上一行主元的列索引（形成“階梯”結構）；
3. 主元下方的所有元素全為 $0$；
4. 主元可為任意非零數（無需強制為 $1$）。

示例（主元用橙色標注）：
$$\left(\begin{array}{cccc}2& 3& 5& 7\\ 0& ?1& 4& 2\\ 0& 0& 0& 3\\ 0& 0& 0& 0\end{array}\right)$$

用途：快速判斷矩陣的秩（非零行數 = 秩）；初步求解線性方程組（需后續“回代”步驟）。
注意：一個矩陣的 REF 不唯一（主元可縮放，不同初等行變換可能得到不同 REF）。

2. 行簡化行階梯形（Reduced Row Echelon Form, RREF）

RREF 是 REF 的“最簡形式”，在 REF 規則基礎上額外滿足 2 條嚴格規則：

1. 所有主元的值必為 $1$；
2. 主元上方的所有元素全為 $0$（即主元列僅主元為 $1$，其余元素均為 $0$）。

示例（將上述 REF 化為 RREF，主元用橙色標注）：
$$\left(\begin{array}{cccc}1& 0& 17/2& 0\\ 0& 1& ?4& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right)$$

重要性質：一個矩陣的 RREF 是唯一的（無論采用何種初等行變換，最終結果完全相同）。
用途：直接讀取線性方程組的解（無需回代）；確定矩陣的主元列（對應列空間的基）；判斷向量組的線性相關性。

3. 列階梯形（Column Echelon Form, CEF）

CEF 與 REF 邏輯對稱，通過初等列變換實現，需滿足以下 4 條規則：

1. 全零列位于矩陣最右側；
2. 非零列的第一個非零元素（稱為“列主元”）的行索引，嚴格大于左一列列主元的行索引；
3. 列主元右側的所有元素全為 $0$；
4. 列主元可為任意非零數（無需強制為 $1$）。

示例（列主元用橙色標注）：
$$\left(\begin{array}{cccc}2& 0& 0& 0\\ 3& ?1& 0& 0\\ 5& 4& 0& 0\\ 7& 2& 3& 0\end{array}\right)$$

用途：分析矩陣的行空間（非零行是行空間的基）；計算矩陣的左逆（當矩陣列滿秩時）。

4. 等價標準形（相抵標準形）

若同時允許初等行變換和初等列變換，任意 $m\times n$ 矩陣可化為唯一的“等價標準形”，形式為：
$$\mathbf{E}=\left(\begin{array}{cc}{\mathbf{I}}_r& 0_{r\times (n?r)}\\ 0_{(m?r)\times r}& 0_{(m?r)\times (n?r)}\end{array}\right)$$
其中：

• $m,n$ 分別為原矩陣的行數和列數；
• $r=R(A)$（矩陣的秩）；
• ${\mathbf{I}}_r$ 為 $r$ 階單位矩陣，$0$ 為對應維度的零矩陣。

示例（秩為 $2$ 的 $3\times 4$ 矩陣的等價標準形）：
$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

用途：判斷兩個矩陣是否“等價”（若兩個矩陣的等價標準形相同，則二者等價）；簡化矩陣的秩與行列式計算。

（三）矩陣化簡的應用場景總結

為清晰區分不同化簡形式的適用場景，下表梳理了重要信息：

化簡目標	推薦化簡形式	操作方式	典型用途
快速計算矩陣的秩	行階梯形（REF）	初等行變換	初步分析矩陣的有效維度，判斷向量組線性相關性
求解線性方程組	行簡化行階梯形（RREF）	初等行變換	直接讀取唯一解或無窮解的通解，無需回代
確定列空間的基	行簡化行階梯形（RREF）	初等行變換	主元列對應原矩陣的列向量，構成列空間的基
確定行空間的基	列階梯形（CEF）	初等列變換	主元行對應原矩陣的行向量，構成行空間的基
判斷兩個矩陣是否等價	等價標準形	初等行變換 + 初等列變換	比較兩個矩陣的結構相似度，驗證是否可通過初等變換互化

四、矩陣秩的性質

設 $A$、$B$ 為任意矩陣，$k$ 為非零常數，$n$ 為方陣的階數，則矩陣的秩滿足以下性質，下表結合“性質內容”與“直觀說明”展開：

性質序號	性質內容	說明
1	$R(A^T)=R(A)$（轉置后秩不變）	矩陣的行秩 = 列秩，轉置后行與列互換，秩的本質（線性無關向量的最大個數）不變
2	R(A)≤min?{m,n}R(A) \leq \min\{m, n\}R(A)≤min{m,n}（$A$ 為 $m\times n$ 矩陣）	秩反映矩陣的“有效維度”，無法超過矩陣的行數（行向量最大可能無關個數）或列數（列向量最大可能無關個數）
3	$R(kA)=R(A)$（$k\ne 0$）	非零常數 $k$ 僅縮放矩陣元素，不改變子式的“非零性”（非零子式縮放后仍非零，零子式縮放后仍為零）
4	$R(A)=0?A=0$（零矩陣的充要條件）	零矩陣所有子式均為 $0$，故秩為 $0$；若 $R(A)=0$，則無任何非零子式，矩陣必為零矩陣
5	$R(A+B)\le R(A)+R(B)$（和的秩不超過秩的和）	矩陣 $A+B$ 的行向量可由 $A$ 和 $B$ 的行向量組線性表示，因此其線性無關向量的最大個數不超過兩組向量無關個數之和
6	R(AB)≤min?{R(A),R(B)}R(AB) \leq \min\{R(A), R(B)\}R(AB)≤min{R(A),R(B)}（乘積的秩不超過因子矩陣的秩）	$AB$ 的列向量可由 $A$ 的列向量線性表示（故 $R(AB)\le R(A)$），行向量可由 $B$ 的行向量線性表示（故 $R(AB)\le R(B)$），因此取最小值
7	$R(A)+R(B)?n\le R(AB)$（Sylvester 不等式）	對 $n$ 階方陣 $A$、$B$，乘積的秩存在下界，反映了因子矩陣秩與乘積矩陣秩的“關聯約束”，可用于證明矩陣可逆性等問題
8	若 $A$ 為 $n$ 階可逆矩陣，則 $R(AB)=R(B)$，$R(BA)=R(B)$	可逆矩陣可通過初等變換化為單位陣，而初等變換不改變矩陣的秩，因此 $A$ 的可逆性不影響 $B$ 的秩傳遞

五、矩陣秩的應用

矩陣的秩是連接“矩陣結構”與“線性代數問題”的橋梁，以下從四個典型場景展開，結合示例說明其應用邏輯：

（一）判斷線性方程組的解

對于線性方程組 $A\mathbf{x}=\mathbf{b}$（$A$ 為 $m\times n$ 系數矩陣，$\overline{A}=(A\mid \mathbf{b})$ 為增廣矩陣），解的存在性與唯一性完全由 $R(A)$ 和 $R(\overline{A})$ 的關系決定，重要結論如下：

1. 無解：$R(A)<R(\overline{A})$（增廣矩陣的秩比系數矩陣多 $1$，對應矛盾方程 $0=d\ne 0$，即“約束條件沖突”）；
2. 唯一解：$R(A)=R(\overline{A})=n$（秩等于未知數個數，無自由變量，即“約束條件恰好確定唯一解”）；
3. 無窮多解：$R(A)=R(\overline{A})<n$（秩小于未知數個數，存在自由變量，即“約束條件不足，解有多個”）。

示例：判斷方程組 $?\begin{array}{l}{x}_1+4x_2+7x_3=1\\ 2x_1+5x_2+8x_3=2\\ 3x_1+6x_2+9x_3=3\end{array}$ 的解

• 第一步：構造增廣矩陣 $\overline{A}=\left(\begin{array}{cccc}1& 4& 7& 1\\ 2& 5& 8& 2\\ 3& 6& 9& 3\end{array}\right)$；
• 第二步：初等行變換化為行階梯形：
  $\overline{A}\stackrel{r_2?2r_1}{\to }\left(\begin{array}{cccc}1& 4& 7& 1\\ 0& ?3& ?6& 0\\ 3& 6& 9& 3\end{array}\right)\stackrel{r_3?3r_1}{\to }\left(\begin{array}{cccc}1& 4& 7& 1\\ 0& ?3& ?6& 0\\ 0& ?6& ?12& 0\end{array}\right)\stackrel{r_3?2r_2}{\to }\left(\begin{array}{cccc}1& 4& 7& 1\\ 0& ?3& ?6& 0\\ 0& 0& 0& 0\end{array}\right)$；
• 第三步：分析秩的關系：$R(A)=2$，$R(\overline{A})=2$，且未知數個數 $n=3$，滿足 $R(A)=R(\overline{A})<n$，因此方程組有無窮多解。

（二）判斷向量組的線性相關性

設向量組 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_s$ 構成矩陣 $A$（列向量組構成 $A=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_s)$，行向量組構成 $A=\left(\begin{array}{c}{\alpha }_1^T\\ {\alpha }_2^T\\ \dots \\ {\alpha }_s^T\end{array}\right)$），則向量組的線性相關性與 $R(A)$ 的關系為：

1. 若 $R(A)=s$，則向量組 線性無關（矩陣的秩等于向量個數，所有向量均可作為“有效約束”，無冗余）；
2. 若 $R(A)<s$，則向量組 線性相關（矩陣的秩小于向量個數，存在冗余向量，可由其他向量線性表示）。

示例：判斷向量組 ${\alpha }_1=(1,2,3{)}^T$，${\alpha }_2=(2,5,8{)}^T$，${\alpha }_3=(3,6,9{)}^T$ 的線性相關性

• 構造矩陣 $A=({\alpha }_1,{\alpha }_2,{\alpha }_3)=\left(\begin{array}{ccc}1& 2& 3\\ 2& 5& 6\\ 3& 8& 9\end{array}\right)$；
• 初等行變換化為行階梯形：$A\stackrel{r_2?2r_1}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& 1& 0\\ 3& 8& 9\end{array}\right)\stackrel{r_3?3r_1}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& 1& 0\\ 0& 2& 0\end{array}\right)\stackrel{r_3?2r_2}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& 1& 0\\ 0& 0& 0\end{array}\right)$；
• 得 $R(A)=2<3$（向量個數），因此向量組線性相關。

（三）判斷矩陣的可逆性

對 $n$ 階方陣 $A$，“可逆性”與“秩”緊密關聯，以下條件完全等價（可互相推導）：

1. $A$ 可逆（存在逆矩陣 $A^{?1}$，滿足 $A{A}^{?1}=A^{?1}A={\mathbf{I}}_n$）；
2. $A$ 為滿秩矩陣（$R(A)=n$，即矩陣無冗余行/列，有效維度等于階數）；
3. $\det (A)\ne 0$（行列式非零，對應“最高階子式非零”，符合滿秩定義）；
4. $A$ 可通過初等行變換化為單位陣 ${\mathbf{I}}_n$（初等變換不改變秩，單位陣秩為 $n$，故 $A$ 秩也為 $n$）。

示例：設 $A=\left(\begin{array}{ccc}1& 2& 3\\ 2& 1& 2\\ 3& 1& 2\end{array}\right)$，驗證 $A$ 可逆并化為單位陣

• 第一步：計算 $R(A)$：
  $A\stackrel{r_2?2r_1}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& ?3& ?4\\ 3& 1& 2\end{array}\right)\stackrel{r_3?3r_1}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& ?3& ?4\\ 0& ?5& ?7\end{array}\right)\stackrel{r_3?\frac{5}{3}{r}_2}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& ?3& ?4\\ 0& 0& ?\frac{1}{3}\end{array}\right)$；
• 行階梯形中非零行數為 $3=n$（階數），故 $R(A)=3$，$A$ 可逆；
• 第二步：繼續化為單位陣：
  $\stackrel{r_3\times (?3)}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& ?3& ?4\\ 0& 0& 1\end{array}\right)\stackrel{r_2+4r_3}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& ?3& 0\\ 0& 0& 1\end{array}\right)\stackrel{r_2\times (?\frac{1}{3})}{\to }\left(\begin{array}{ccc}1& 2& 3\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\stackrel{r_1?3r_3}{\to }\left(\begin{array}{ccc}1& 2& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\stackrel{r_1?2r_2}{\to }\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)={\mathbf{I}}_3$。

（四）數據降維和信息壓縮

在機器學習、信號處理等領域，矩陣的秩反映“數據冗余度”：低秩矩陣（R(A)?min?{m,n}R(A) \ll \min\{m, n\}R(A)?min{m,n}）表示數據存在大量冗余，可通過“保留核心信息、剔除冗余”實現降維與壓縮，典型應用為奇異值分解（SVD） 和主成分分析（PCA）。

• 邏輯：對矩陣 $A$ 進行奇異值分解，得 $A=U\Sigma V^T$，其中 $\Sigma$ 為對角矩陣，對角元素（奇異值）按從大到小排列；取前 $r$ 個非零奇異值（$r=R(A)$）對應的子矩陣，可得到原矩陣的低秩逼近 $A_r=U_r{\Sigma }_r{V}_r^T$，實現用 $r(m+n?r)$ 個元素表示原 $m\times n$ 矩陣（大幅減少存儲量）。
• 示例：圖片壓縮。灰度圖片可表示為 $m\times n$ 矩陣（元素為像素灰度值），若矩陣秩 $r$ 遠小于 $m$ 和 $n$，用低秩逼近矩陣 $A_r$ 替代原矩陣，視覺上幾乎無差異，但存儲量顯著降低。

六、特殊矩陣的秩

部分結構特殊的矩陣，其秩可直接通過“直觀特征”計算，無需復雜變換，以下列舉兩類典型矩陣：

（一）三角矩陣

三角矩陣分為上三角矩陣和下三角矩陣，其秩由“主對角線元素”直接決定：

• 上三角矩陣（主對角線下方元素全為 $0$）：$\left(\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ 0& a_{22}& \dots & a_{2n}\\ ?& ?& ?& ?\\ 0& 0& \dots & a_{nn}\end{array}\right)$；
• 下三角矩陣（主對角線上方元素全為 $0$）：$\left(\begin{array}{cccc}{a}_{11}& 0& \dots & 0\\ a_{21}& a_{22}& \dots & 0\\ ?& ?& ?& ?\\ a_{n1}& a_{n2}& \dots & a_{nn}\end{array}\right)$；
• 秩的計算規則：三角矩陣的秩等于主對角線上非零元素的個數。
  （原因：三角矩陣的行列式為“主對角線元素乘積”，最高階非零子式的階數由非零對角元素的個數決定）。

示例：上三角矩陣 $A=\left(\begin{array}{ccc}2& 3& 5\\ 0& 0& 4\\ 0& 0& ?1\end{array}\right)$，主對角線元素為 $2,0,?1$，非零個數為 $2$，故 $R(A)=2$。

（二）對角矩陣

對角矩陣是特殊的三角矩陣（主對角線外元素全為 $0$），形式為：$\left(\begin{array}{cccc}{a}_{11}& 0& \dots & 0\\ 0& a_{22}& \dots & 0\\ ?& ?& ?& ?\\ 0& 0& \dots & a_{nn}\end{array}\right)$；

• 秩的計算規則：對角矩陣的秩等于對角線上非零元素的個數（與三角矩陣規則一致，因對角矩陣同時屬于上三角矩陣和下三角矩陣）。

示例：對角矩陣 $B=\left(\begin{array}{ccc}?3& 0& 0\\ 0& 0& 0\\ 0& 0& 5\end{array}\right)$，對角線上非零元素為 $?3$ 和 $5$，共 $2$ 個，故 $R(B)=2$。

七、MATLAB 計算矩陣秩的代碼實現

在 MATLAB 中，可直接使用內置函數 rank() 快速計算矩陣的秩，其底層通過奇異值分解（SVD）實現，能有效避免數值誤差對結果的影響。以下為具體實現步驟與示例：

% 1. 定義矩陣 A（以 3×3 矩陣為例）
A = [1 2 3; 4 5 6; 7 8 9];% 2. 計算矩陣 A 的秩
rank_A = rank(A);% 3. 顯示結果
disp(['矩陣 A 的秩為: ', num2str(rank_A)]);

運行結果：矩陣 A 的秩為: 2（與通過初等變換手動計算的結果一致）。

說明：

• rank() 函數的邏輯是：對矩陣進行奇異值分解，得到奇異值后，將小于某個閾值（默認約為 $10^{?15}$）的奇異值視為 $0$，非零奇異值的個數即為矩陣的秩；
• 閾值可通過函數參數調整，例如 rank(A, tol) 中 tol 為自定義閾值，適用于對數值精度有特殊要求的場景；
• 該函數適用于任意維度的矩陣（包括非方陣），是工程計算中高效可靠的秩計算工具。

八、例題解析：矩陣秩的應用

（一）題目

已知行簡化行階梯形矩陣 $A=\left(\begin{array}{cccc}1& 2& 0& 4\\ 0& 0& 1& 3\\ 0& 0& 0& 0\end{array}\right)$，完成以下任務：

1. 求 $A$ 的秩；
2. 求 $A$ 的行秩并驗證其與秩的關系；
3. 求 $A$ 的列秩并驗證其與秩的關系。

（二）解答過程

1. 求矩陣 $A$ 的秩

根據“行階梯形矩陣的秩等于非零行的行數”這一結論：

• 矩陣 $A$ 中，非零行包括第 1 行 $\left(\begin{array}{cccc}1& 2& 0& 4\end{array}\right)$ 和第 2 行 $\left(\begin{array}{cccc}0& 0& 1& 3\end{array}\right)$，共 $2$ 行；
• 零行僅第 3 行 $\left(\begin{array}{cccc}0& 0& 0& 0\end{array}\right)$，且位于所有非零行下方（符合行階梯形結構）。

因此，$R(A)=2$。

2. 求矩陣 $A$ 的行秩

矩陣 $A$ 的行向量組為：
$${\alpha }_1=(1,2,0,4),{\alpha }_2=(0,0,1,3),{\alpha }_3=(0,0,0,0)$$

行秩是“行向量組中線性無關的最大向量個數”，分析如下：

• 線性無關性驗證：假設存在常數 $k_1,k_2$ 使得 $k_1{\alpha }_1+k_2{\alpha }_2=0$（零向量），展開得：
  $$(k_1,2k_1,k_2,4k_1+3k_2)=(0,0,0,0)$$
  解得 $k_1=0$ 且 $k_2=0$，故 ${\alpha }_1,{\alpha }_2$ 線性無關；
• 最大性驗證：零向量 ${\alpha }_3$ 可由 ${\alpha }_1,{\alpha }_2$ 線性表示（${\alpha }_3=0?{\alpha }_1+0?{\alpha }_2$），因此行向量組中線性無關的最大向量個數為 $2$。

因此，$A$ 的行秩為 $2$，且 $R(A)=\text{行秩}$。

3. 求矩陣 $A$ 的列秩

矩陣 $A$ 的列向量組為：
$${\beta }_1=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),{\beta }_2=\left(\begin{array}{c}2\\ 0\\ 0\end{array}\right),{\beta }_3=\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),{\beta }_4=\left(\begin{array}{c}4\\ 3\\ 0\end{array}\right)$$

列秩是“列向量組中線性無關的最大向量個數”，分析如下（選取主元列 ${\beta }_1,{\beta }_3$ 驗證）：

• 線性無關性驗證：假設存在常數 $l_1,l_3$ 使得 $l_1{\beta }_1+l_3{\beta }_3=0$（零向量），展開得：
  $$\left(\begin{array}{c}{l}_1\\ l_3\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$$
  解得 $l_1=0$ 且 $l_3=0$，故 ${\beta }_1,{\beta }_3$ 線性無關；
• 最大性驗證：非主元列可由主元列線性表示：
  • ${\beta }_2=2{\beta }_1+0?{\beta }_3$，${\beta }_4=4{\beta }_1+3{\beta }_3$，因此列向量組中線性無關的最大向量個數為 $2$。

因此，$A$ 的列秩為 $2$，且 $R(A)=\text{列秩}=\text{行秩}$。

（三）結論

通過例題驗證，矩陣的秩、行秩與列秩三者完全相等，這一性質是矩陣理論的重要結論，也是理解矩陣結構與向量組關系的關鍵。

九、總結

矩陣的秩是線性代數中刻畫矩陣“本質維度”的重要概念，其定義基于子式的非零性，計算可通過子式判別法或更高效的初等變換法實現。矩陣的秩具有諸多重要性質，如轉置不變性、乘積秩的有界性等，這些性質為分析矩陣關系提供了有力工具。

在應用層面，矩陣的秩決定了線性方程組解的存在性與唯一性，可判斷向量組的線性相關性，驗證矩陣的可逆性，同時在數據降維、信息壓縮等領域有廣泛應用。掌握矩陣秩的概念、計算方法與應用場景，是學好線性代數的重要基礎。

---

從兩個角度看矩陣和向量相乘

Limi @_zhihu

前提條件

設矩陣 $A$ 與向量 $x$ 進行乘法運算，結果為向量 $b$，其維度與 $x$ 相同。進行此乘法運算的前提條件是矩陣 $A$ 的列數等于向量 $x$ 的行數。以下從兩個方面探討如何求得 $b$ ：行視角（Row Aspect）和列視角（Column Aspect）。

行視角（Row Aspect）

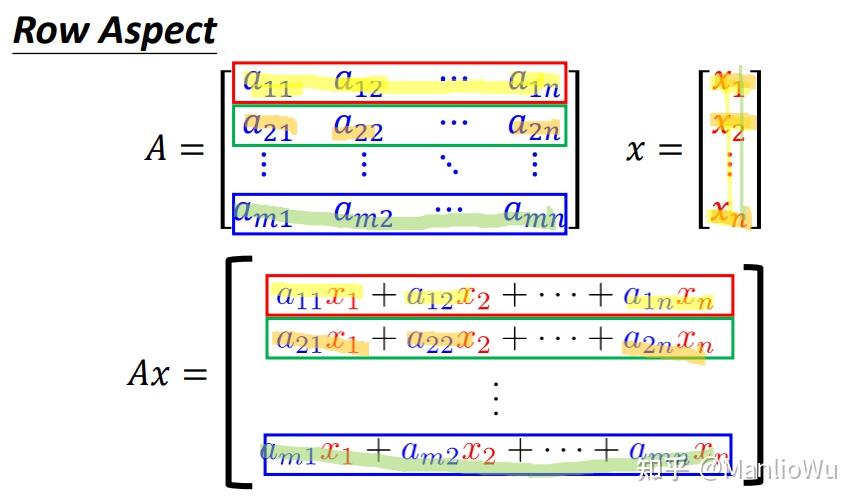
將矩陣 $A$ 視作“行向量的堆疊”，即 $A$ 的每一行均為一個向量。則向量 $b$ 的第 $i$ 個維度的值為 $A$ 的第 $i$ 行向量與 $x$ 作內積的結果，即 $b_i=(A_i,x)$ 。內積運算要求兩個向量的維度相同，這也解釋了矩陣與向量相乘時矩陣列數與向量行數需相等的原因。此外，在矩陣 $\times$ 矩陣的運算中，常采用的計算方法為：矩陣 $A$ 的第 $i$ 行與矩陣 $B$ 的第 $j$ 列相乘，結果為 $C_{i,j}$ 。矩陣 $\times$ 向量可視為矩陣 $\times$ 矩陣的特殊情形，即右側矩陣僅有一列。

列視角（Column Aspect）

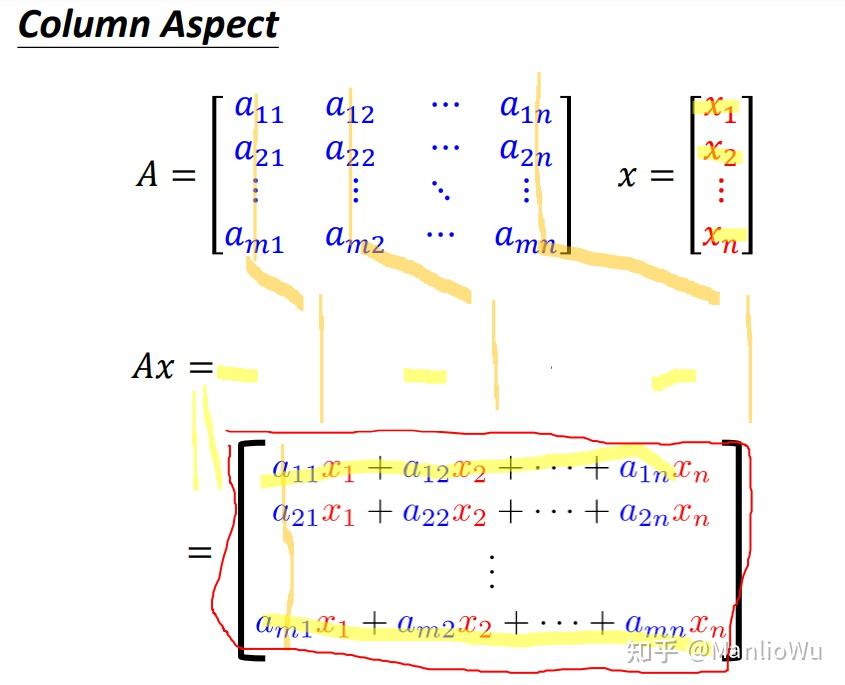
將矩陣 $A$ 視作“列向量的并列”，即每一列均為一個向量。以向量 $x$ 的第 $i$ 個元素乘以矩陣 $A$ 的第 $i$ 個列向量，可得到 $n$ 個向量（若矩陣 $A$ 有 $n$ 列）。將這 $n$ 個向量相加，即得結果 $b$ ，表達式為

$$b=\sum _{i=1}^n{A}_i?x_i$$

其中，$A_i$ 為列向量，$x_i$ 為標量。此方法同樣解釋了矩陣列數與向量行數需相等的原因。該方法可視為對矩陣 $A$ 的 $n$ 個向量進行線性組合以得到新向量，在某些情況下更易于理解。在 3b1b 的線性代數課程中，有一種解釋是將 $A$ 的每個列向量視為向量空間的基向量，向量 $x$ 的每個值為對應基向量的投影長度。將每個投影長度與基向量相乘后再求和，即可得到新向量。

總結與對比

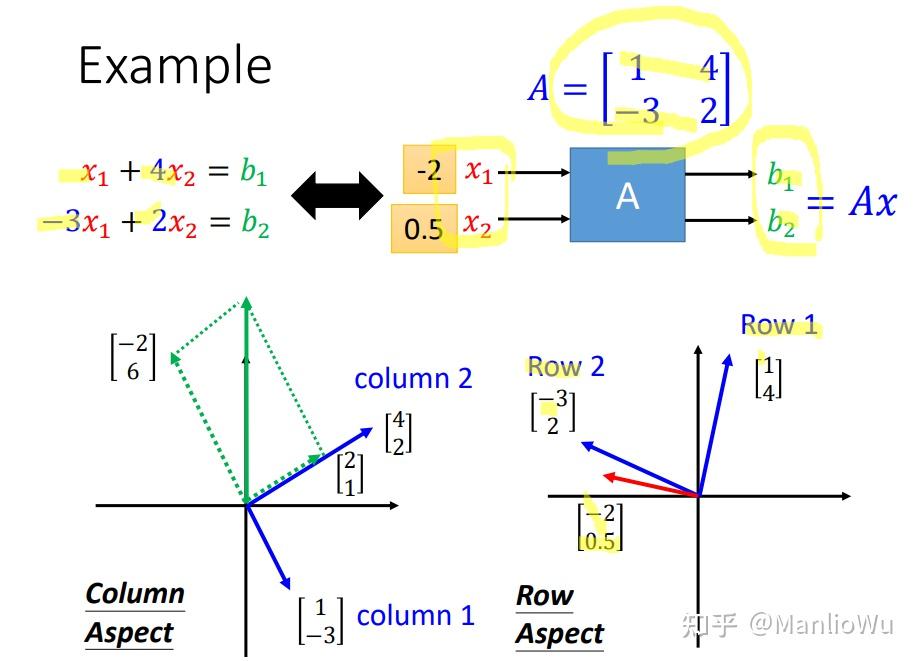
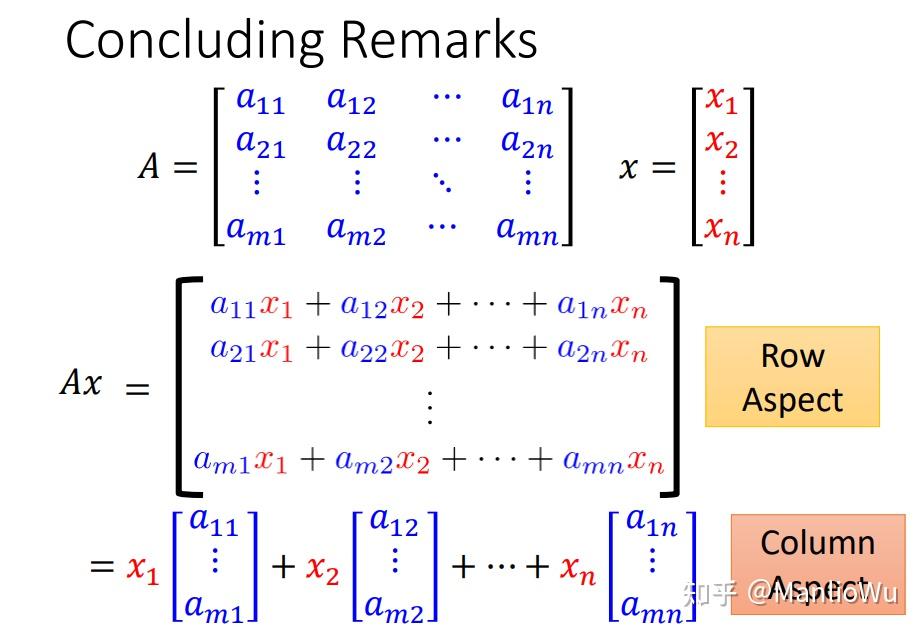
綜合來看，列視角（Column Aspect）在理解矩陣與向量相乘方面更具優勢，具有重要的現實意義。

發布于 2022-08-04 17:14?廣東

---

矩陣的秩以及行秩 = 列秩的原因

Limi @_zhihu

在矩陣理論中，矩陣的秩是一個重要概念，廣泛應用于多個數學分支。矩陣的秩定義為矩陣中線性無關行向量或列向量的最大數目。具體來說，矩陣 $A$ 的列秩是其線性無關列向量的最大數目，而行秩是其線性無關行向量的最大數目。這兩個定義是等價的，即矩陣的秩等于其行秩也等于其列秩。

用數學符號表示，矩陣 $A$ 的秩通常記作 $r(A)$、$\text{rk}(A)$ 或 $\text{rank}A$。矩陣的秩反映了矩陣中線性無關向量的最大數量，這一數量決定了矩陣的“厚度”或“維度”。

對于矩陣 $A_{m\times n}$，可以將其視為由 $n$ 個列向量組成的矩陣。每個列向量對應一個基底，因此極大線性無關組的列向量個數（矩陣的秩）也稱為列空間（Column Space）的維度。

在求解矩陣的秩時，通常通過基本行變換將其轉換為階梯矩陣。在階梯矩陣中，每一行的第一個非零元素的列數依次向右移動（全零行除外）。即第 $i+1$ 行的第一個非零元素位于第 $i$ 行第一個非零元素的右下方。矩陣的秩 $r$ 等于階梯矩陣中單位向量（unit vector）的個數。單位向量是指向量中只有一個元素為 1，其余元素均為 0，也稱為基向量（pivot column）或標準向量（standard vector），類似于 one-hot 編碼。例如，$[1,0,0]$ 和 $[0,1,0]$ 均為單位向量。

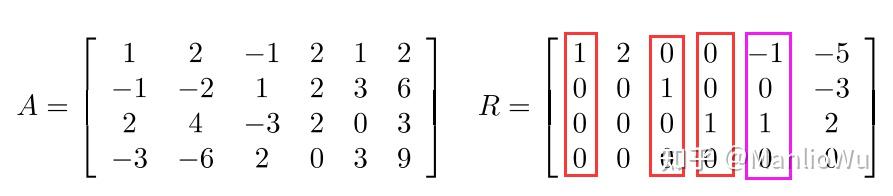
如圖所示，左側為原始矩陣，右側為階梯矩陣。階梯矩陣中有 3 個單位向量（紅色框標記），因此列秩為 3。紫色向量為何不能計入矩陣的極大線性無關組呢？因為其非零元素出現的位置并非對應行的第一個，即在其左側存在單位向量，該向量可由其左側的單位向量線性表示。例如，圖中的矩陣 $[?1,0,1,0]=?1\times [1,0,0,0]+0\times [0,1,0,0]+1\times [0,0,1,0]$。線性無關向量組中的向量不能相互表示，因此紫色向量不能計入。

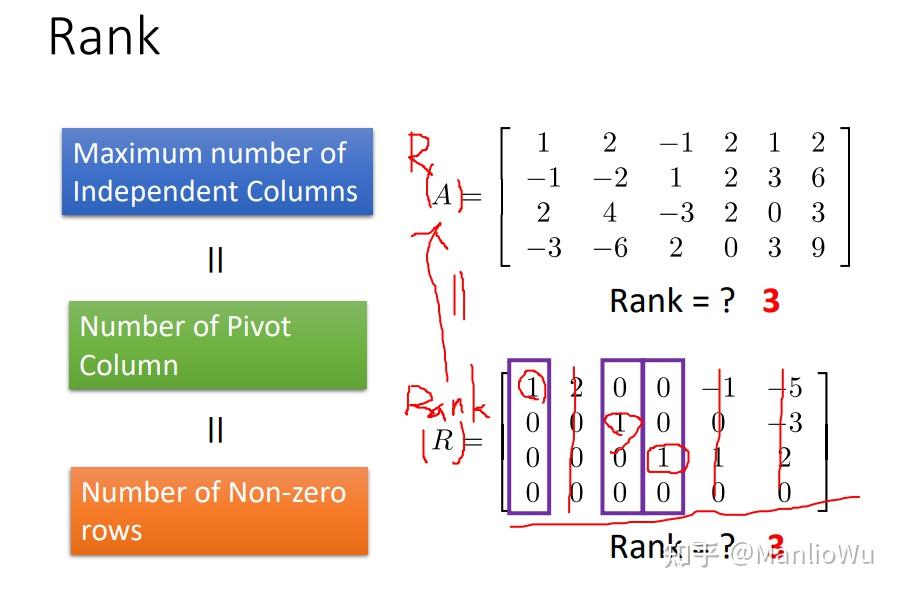
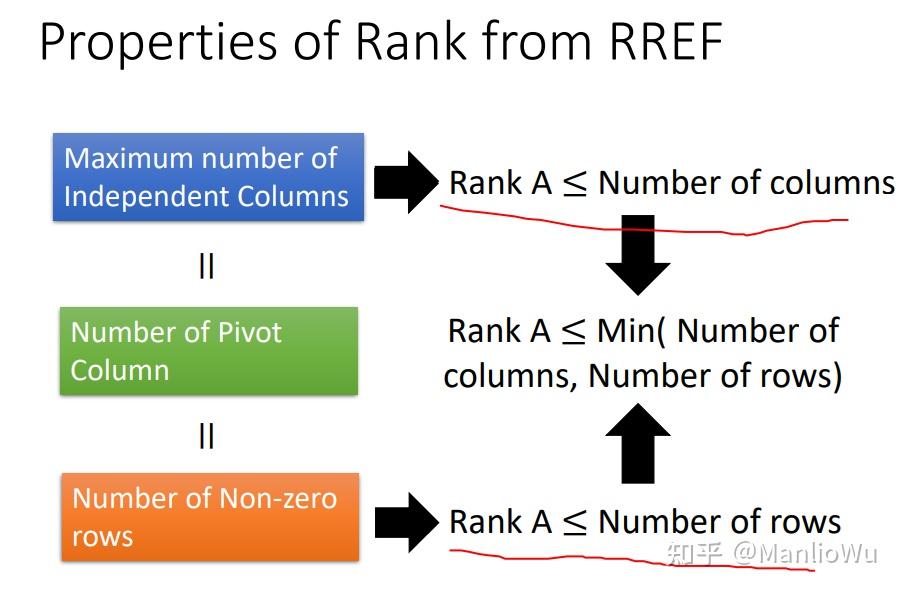
通過上述例子可知，單位向量的特點是：該向量中 1 的位置是其所在行的第一個非零元素。階梯矩陣中單位向量的個數即為矩陣的秩。進一步分析可得，“第一個出現的非零元素” 的個數等于非零行的行數，即行秩。因此，矩陣的行秩等于列秩。此外，還可得出 rank(A)≤min?{m,n}\text{rank}(A) \leq \min\{m, n\}rank(A)≤min{m,n}。

總結如下圖：

三種典型的子空間

列空間（Column Space）與行空間（Row Space）與零空間（Null Space）

對于零空間（Null Space），即 $Ax=0$ 的基礎解系構成的空間。以下是一個例子，其中存在 2 個自由變量（free variable），可得兩個基向量（basis），因此零空間的維度為 2。矩陣的秩為 3，滿足 $\text{rank}(A)+\text{dimension}(\text{Null?space})=n$。

具體分析如下：共有 $n$ 個變量，其中 $k$ 個為自由變量，其余 $n?k$ 個變量可直接確定。在由 $k$ 個自由變量構成的 $k$ 維空間中，任取一個向量，再與 $n?k$ 個確定的值組合，即可得到 $Ax=0$ 的解。從另一個角度理解，存在 $k$ 個自由變量，是因為在階梯矩陣中，有 $k$ 個列向量可由其余 $n?k$ 個基向量（pivot columns）線性表示。因此，給定一組 $n?k$ 個值，即可求得一組 $k$ 個值。綜合所有情況，可形成一個 $k$ 維空間。

單位向量（unit vector）的重要作用

單位向量是指向量中僅有一個位置為 1，其余位置均為 0。對于 $n$ 維向量，存在 $n$ 個單位向量。按“1” 的位置從小到大排序，分別為 $e_1,e_2,e_3,\dots ,e_n$。其中，$e_1=[1,0,0,\dots ,0{]}^T$，$e_2=[0,1,0,\dots ,0]$，$\dots$，$e_n=[0,0,0,\dots ,1{]}^T$。

利用這些單位向量可“提取矩陣”。具體而言，$A{e}_i$ 得到的向量是矩陣 $A$ 的第 $i$ 列。以下是一個示例：

$$\left[\begin{array}{cc}0& 1\\ ?1& 0\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ ?1\end{array}\right]\left[\begin{array}{cc}0& 1\\ ?1& 0\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]$$

矩陣與向量相乘可視為向量與其對應投影長度的乘積。單位向量 $e_i$ 僅在第 $i$ 個位置為 1，其余位置為 0，因此只有矩陣 $A$ 的第 $i$ 個列向量的投影長度為 1，其余投影長度為 0，從而可提取矩陣 $A$ 的第 $i$ 列。

編輯于 2022-08-07 20:16

---

線性代數 —— 矩陣的列秩和行秩

原創于 2019-09-04 19:20:42 發布

1. 矩陣的列秩和行秩及秩的關系（行秩 = 列秩 = 秩）

2. 初等行變換不改變矩陣的線性相關性

3. 任一矩陣的秩、行秩和列秩相等

4. 求矩陣列向量組的秩及最大無關組示例

---

via:

• 矩陣秩的計算方法-CSDN博客
  https://blog.csdn.net/edward_zcl/article/details/90177159

• 矩陣的秩及其求法-CSDN博客
  https://blog.csdn.net/qq_55342245/article/details/120188405

• 什么是矩陣的秩，矩陣的秩如何計算？-CSDN博客
  https://blog.csdn.net/weixin_44114030/article/details/143424474

• 從兩個角度看矩陣和向量相乘 - 知乎
  https://zhuanlan.zhihu.com/p/549884913

• 矩陣的秩以及為什么行秩=列秩 - 知乎
  https://zhuanlan.zhihu.com/p/550019600

• 線性代數學習筆記——矩陣的列秩和行秩_行秩和列秩怎么求-CSDN博客
  https://blog.csdn.net/hpdlzu80100/article/details/100545450