目錄
1.什么是跳表-skiplist
2.skiplist的效率如何保證?
3.skiplist的實現
3.1節點和成員設計
3.2查找實現
3.3前置節點查找
3.4插入實現
3.5刪除實現
3.6隨機層數
3.7完整代碼
4.skiplist跟平衡搜索樹和哈希表的對比
1.什么是跳表-skiplist
skiplist是由William Pugh發明的,最早出現于他在1990年發表的論文《Skip Lists: A
Probabilistic Alternative to Balanced Trees》。
skiplist,顧名思義,首先它是一個list。實際上,它是在有序鏈表的基礎上發展起來的。如果是一個有序的鏈表,查找數據的時間復雜度是O(N)。
William Pugh開始的優化思路:
1. 假如我們每相鄰兩個節點升高一層,增加一個指針,讓指針指向下下個節點,如下圖b所
示。這樣所有新增加的指針連成了一個新的鏈表,但它包含的節點個數只有原來的一半。由
于新增加的指針,我們不再需要與鏈表中每個節點逐個進行比較了,需要比較的節點數大概
只有原來的一半。2. 以此類推,我們可以在第二層新產生的鏈表上,繼續為每相鄰的兩個節點升高一層,增加一個指針,從而產生第三層鏈表。如下圖c,這樣搜索效率就進一步提高了。
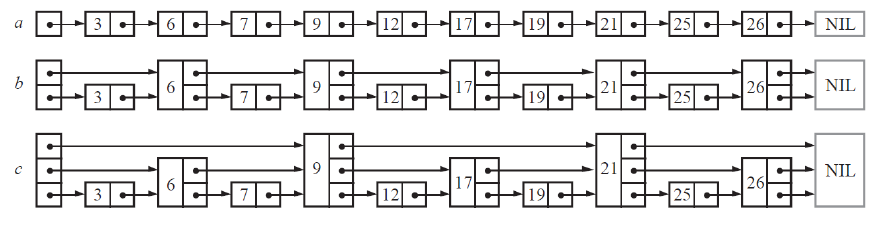
如圖b中,查找8,從頭結點出發,6比8小,向右走,跳躍到6;8比9小,當前節點向下走,從下面指針出發,7比8小,跳轉到7;8比9小,向下走,走不了了,鏈表中不存在8.
如圖c中,查找19,比9大,向右走,跳躍到9;比21小,向下走,比17大,向右走,跳躍到17,比17大,向右走,跳躍到17,比21小,向下走,跟19相等,找到了。
3. skiplist正是受這種多層鏈表的想法的啟發而設計出來的。實際上,按照上面生成鏈表的方
式,上面每一層鏈表的節點個數,是下面一層的節點個數的一半,這樣查找過程就非常類似
二分查找,使得查找的時間復雜度可以降低到O(log n)。但是這個結構在插入刪除數據的時
候有很大的問題,插入或者刪除一個節點之后,就會打亂上下相鄰兩層鏈表上節點個數嚴格
的2:1的對應關系。如果要維持這種對應關系,就必須把新插入的節點后面的所有節點(也
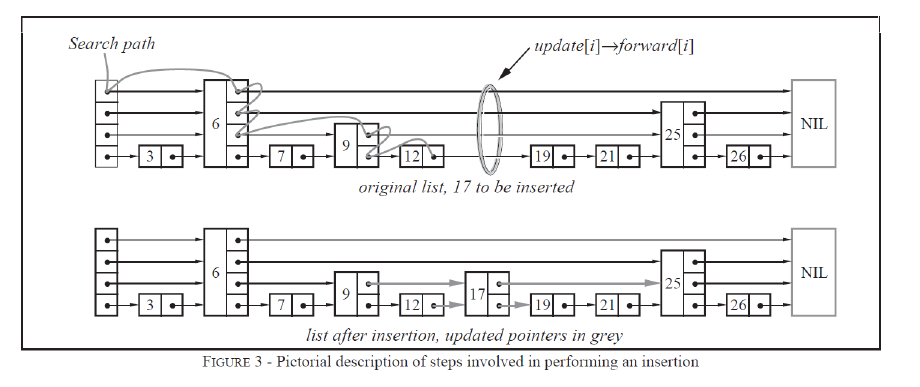
包括新插入的節點)重新進行調整,這會讓時間復雜度重新蛻化成O(n)。4. skiplist的設計為了避免這種問題,做了一個大膽的處理,不再嚴格要求對應比例關系,而是插入一個節點的時候隨機出一個層數。這樣每次插入和刪除都不需要考慮其他節點的層數,這樣就好處理多了(按時插入刪除,我們仍然需要考慮其他節點對應層指針的連接問題)。細節過程入下圖:
2.skiplist的效率如何保證?
上面我們說到,skiplist插入一個節點時隨機出一個層數,聽起來怎么這么隨意,如何保證搜索時
的效率呢?
這里首先要細節分析的是這個隨機層數是怎么來的。一般跳表會設計一個最大層數maxLevel的限
制,其次會設置一個多增加一層的概率p。那么計算這個隨機層數的偽代碼如下圖:

在Redis的skiplist實現中,這兩個參數的取值為:
p = 1/4
maxLevel = 32根據前面randomLevel()的偽碼,我們很容易看出,產生越高的節點層數,概率越低。定量的分析
如下:
節點層數至少為1。而大于1的節點層數,滿足一個概率分布。
節點層數恰好等于1的概率為1-p。
節點層數大于等于2的概率為p,而節點層數恰好等于2的概率為p(1-p)。
節點層數大于等于3的概率為p^2,而節點層數恰好等于3的概率為p^2*(1-p)。
節點層數大于等于4的概率為p^3,而節點層數恰好等于4的概率為p^3*(1-p)。
……
因此,一個節點的平均層數(也即包含的平均指針數目),計算如下:
現在很容易計算出:
當p=1/2時,每個節點所包含的平均指針數目為2;
當p=1/4時,每個節點所包含的平均指針數目為1.33。
跳表的平均時間復雜度為O(logN),
這個推導的過程較為復雜,需要有一定的數據功底,有興趣的,可以參考以下文章中的講解:
鐵蕾大佬的博客:http://zhangtielei.com/posts/blog-redis-skiplist.html
William_Pugh大佬的論文:ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf
3.skiplist的實現
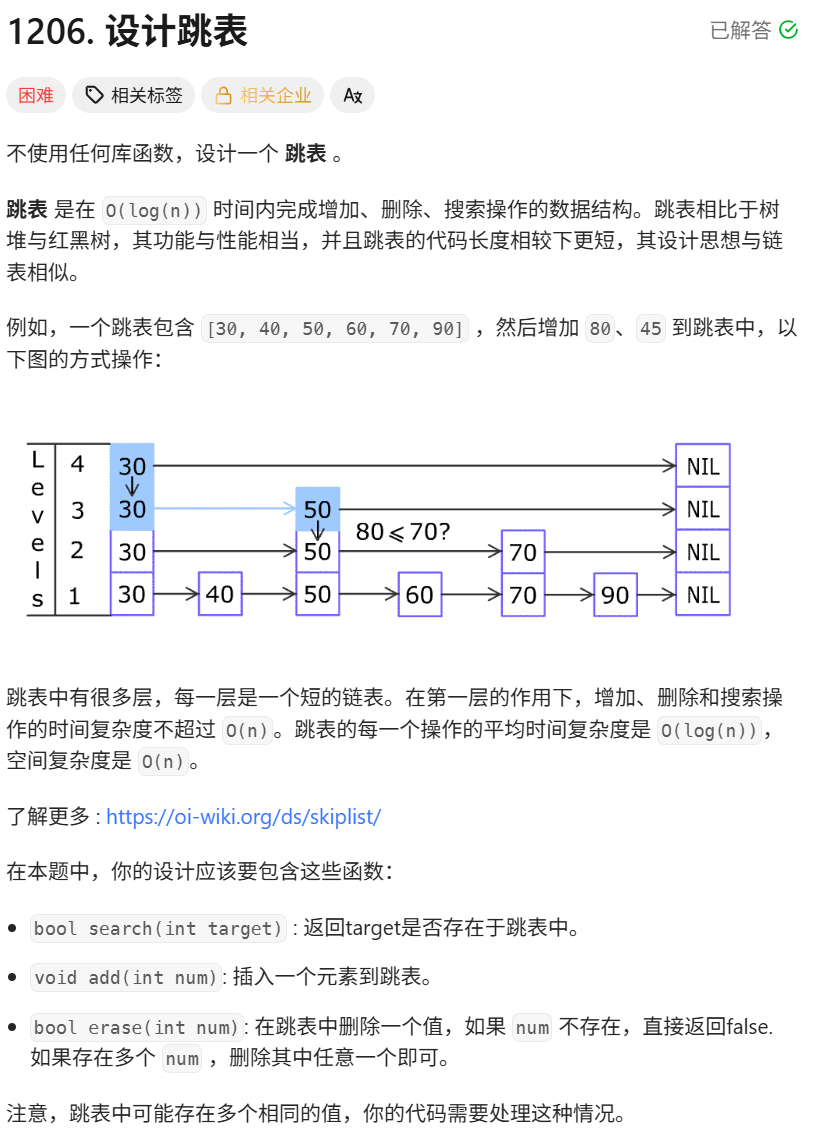
1206. 設計跳表 - 力扣(LeetCode)
3.1節點和成員設計
跳表因為每個節點是層數是隨機的,所以我們使用vector容器存儲對應指針。
對于一開始的同節點,我們這里設計成一層高,減少后續不必要遍歷消耗。
struct SkiplistNode
{int _val;vector<SkiplistNode*> _nextV;SkiplistNode(int val, int level):_val(val), _nextV(level, nullptr){}
};class Skiplist {typedef SkiplistNode Node;
public:Skiplist() {//為了后續層數隨機,這里提供種子srand(time(0));// 頭節點,層數是1_head = new SkiplistNode(-1, 1);}private:Node* _head; // 頭節點size_t _maxLevel = 32;//層數的最大高度double _p = 0.25;/多增加一層的概率p
};3.2查找實現
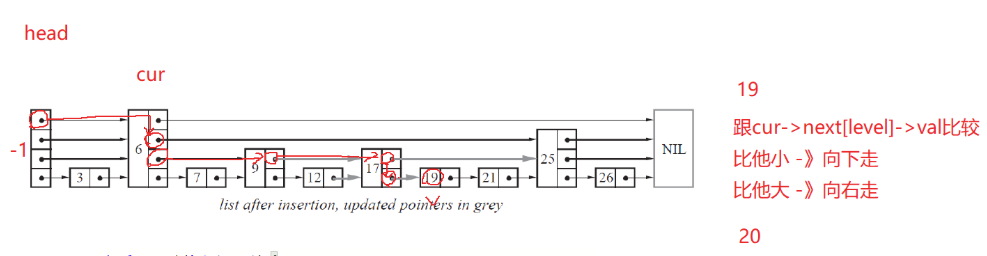
依照跳表的設計,當我們查找一個數時,如果當前層的指針指向的數比要查找的數大,那我們就需要向下走,因為鏈表是有序的,比較小的數一定在前面,而且層高一定沒有當前層指向節點高(如果搞就指向這個更小的數了。)所以我們要找比當前層指向節點小的數,需要向下層走。
反之,如果比當前層指向節點值比要查找的數小,說明要查找的數在后面,我們直接沿當前層指針往后跳轉。
bool search(int target) {Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){// 目標值比下一個節點值要大,向右走// 下一個節點是空(尾),目標值比下一個節點值要小,向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < target){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]-> _val > target){// 向下走--level;}else{return true;}}return false;}3.3前置節點查找
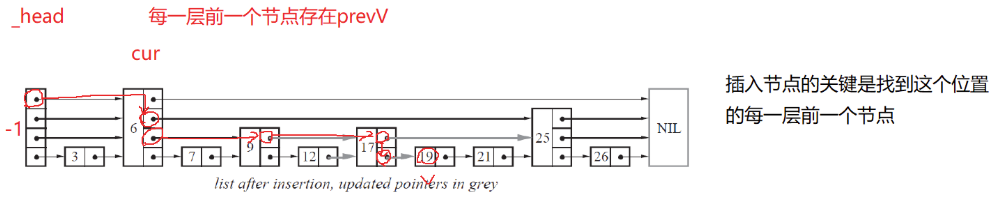
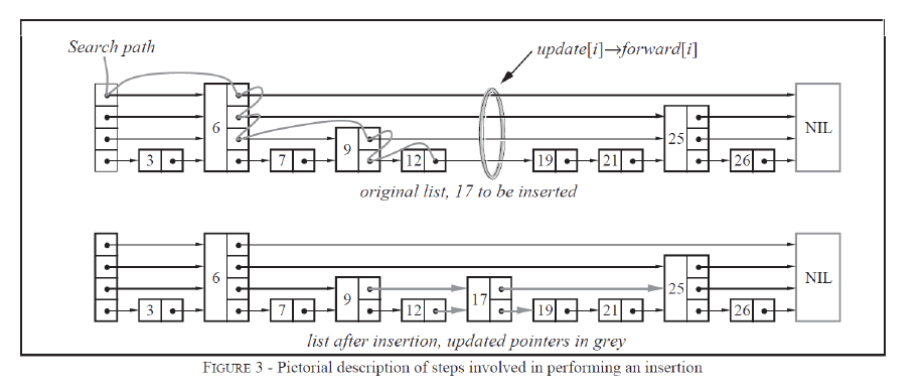
因為跳表中節點的層高沒有嚴格的比例關系,因此一個節點可能由于層高較高,與前后多個節點有關系,如上圖中6有4層,0層上,3指向它,6指向7;1層上頭結點指向6,6指向9;2層上,頭結點指向6,6指向25;3層上頭結點指向6,6指向nullptr。
因此當我們刪除或者增加一個節點,我們就需要建立它每一層上指針與其他節點間關系,同時也需要修改其他其他節點。
這就意味著當前要插入/刪除節點,就需要從整個跳表中找到每一層指針對應的上一個節點,更新指針指向。
解決的思想是利用查找節點過程,因為當一層指針指向空或者比要查找的值大的值時,我們向下走,這同時也意味著此時這層節點就是當前要插入節點的當前層的上一層節點,同時這屆指針指向的下層節點也就是插入節點指針要指向的下一個節點。我們通過查找節點不斷向下走的過程,就能找到插入節點每一層的上一個節點和要指向的下一層節點。
需要注意的是當查找節點比當前節點大,直接跳轉的過程,我們不能更新上一層節點的記錄,因為這是只是同層節點間的跳轉,我們不能確定插入節點當前層的上一個節點。
vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;// 插入位置每一層前一個節點指針vector<Node*> prevV(level + 1, _head);while (level >= 0){// 目標值比下一個節點值要大,向右走// 下一個節點是空(尾),目標值比下一個節點值要小,向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < num){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr|| cur->_nextV[level]->_val >= num){// 更新level層前一個prevV[level] = cur;// 向下走--level;}}return prevV;}3.4插入實現
當我們能找到插入節點的每一層對應上一個節點,我們插入節點只需要更新對應的指向,上一個指針指向它,插入節點指向下一個節點。
這里需要注意的是,插入節點的層數我們封裝一個函數來給在最大范圍內的隨機值,跳表的頭結點需要確保是跳表中最高的節點,這樣才不會出現無法跳轉更高層的問題,所以如果當前的隨機值如果比頭節點高,我們就需要更新下頭結點高度。
void add(int num) {vector<Node*> prevV = FindPrevNode(num);int n = RandomLevel();//隨機層數Node* newnode = new Node(num, n);// 如果n超過當前最大的層數,那就升高一下_head的層數if (n > _head->_nextV.size()){_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}// 鏈接前后節點for (size_t i = 0; i < n; ++i){newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}// Print();}3.5刪除實現
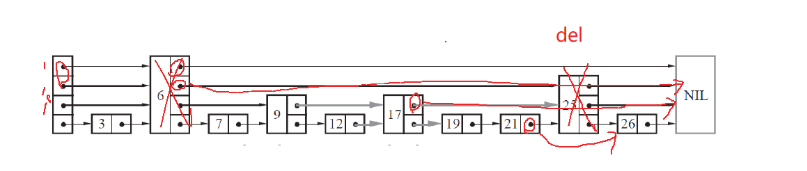
刪除節點后,我們需要根據找到的每一層的上一個節點,更新一下對應指針將刪除節點上一個節點和指向下一個節點相連。
這里加入刪除的節點是最高點,我們更新一下頭結點的高度,避免每次從很高的位置向下遍歷(不過就幾層,相對來說影響不大)。
bool erase(int num) {vector<Node*> prevV = FindPrevNode(num);// 第一層下一個不是val,val不在表中if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val !=num){return false;}else{Node* del = prevV[0]->_nextV[0];// del節點每一層的前后指針鏈接起來for (size_t i = 0; i < del->_nextV.size(); i++){prevV[i]->_nextV[i] = del->_nextV[i];}delete del;// 如果刪除最高層節點,把頭節點的層數也降一下int i = _head->_nextV.size() - 1;while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;}}3.6隨機層數
//產生隨機層數int RandomLevel(){size_t level = 1;//每一個節點最少一層。// 因為rand() ->[0, RAND_MAX]之間,所以RAND_MAX * _p的數出現概率就是p// 可以視作rand()/RAND_MAX <= pwhile (rand() <= RAND_MAX * _p && level < _maxLevel){++level;}return level;}//C++中的隨機函數庫,使用比較麻煩/*int RandomLevel(){static std::default_random_enginegenerator(std::chrono::system_clock::now().time_since_epoch().count());static std::uniform_real_distribution<double> distribution(0.0,1.0);size_t level = 1;while (distribution(generator) <= _p && level < _maxLevel){++level;}return level;}*/3.7完整代碼
struct SkiplistNode
{int _val;vector<SkiplistNode*> _nextV;SkiplistNode(int val, int level):_val(val), _nextV(level, nullptr){}
};
class Skiplist {typedef SkiplistNode Node;
public:Skiplist() {srand(time(0));// 頭節點,層數是1_head = new SkiplistNode(-1, 1);}bool search(int target) {Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){// 目標值比下一個節點值要大,向右走// 下一個節點是空(尾),目標值比下一個節點值要小,向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < target){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr || cur->_nextV[level] -> _val > target){// 向下走--level;}else{return true;}}return false;}vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;// 插入位置每一層前一個節點指針vector<Node*> prevV(level + 1, _head);while (level >= 0){// 目標值比下一個節點值要大,向右走// 下一個節點是空(尾),目標值比下一個節點值要小,向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < num){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr|| cur->_nextV[level]->_val >= num){// 更新level層前一個prevV[level] = cur;// 向下走--level;}}return prevV;}void add(int num) {vector<Node*> prevV = FindPrevNode(num);int n = RandomLevel();Node* newnode = new Node(num, n);// 如果n超過當前最大的層數,那就升高一下_head的層數if (n > _head->_nextV.size()){_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}// 鏈接前后節點for (size_t i = 0; i < n; ++i){newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}// Print();}bool erase(int num) {vector<Node*> prevV = FindPrevNode(num);// 第一層下一個不是val,val不在表中if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val !=num){return false;}else{Node* del = prevV[0]->_nextV[0];// del節點每一層的前后指針鏈接起來for (size_t i = 0; i < del->_nextV.size(); i++){prevV[i]->_nextV[i] = del->_nextV[i];}delete del;// 如果刪除最高層節點,把頭節點的層數也降一下int i = _head->_nextV.size() - 1;while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;}}int RandomLevel(){size_t level = 1;// rand() ->[0, RAND_MAX]之間while (rand() <= RAND_MAX * _p && level < _maxLevel){++level;}return level;}/*int RandomLevel(){static std::default_random_enginegenerator(std::chrono::system_clock::now().time_since_epoch().count());static std::uniform_real_distribution<double> distribution(0.0,1.0);size_t level = 1;while (distribution(generator) <= _p && level < _maxLevel){++level;}return level;}*/private:Node* _head; // 頭節點size_t _maxLevel = 32;double _p = 0.25;
};4.skiplist跟平衡搜索樹和哈希表的對比
1. skiplist相比平衡搜索樹(AVL樹和紅黑樹)對比,都可以做到遍歷數據有序,時間復雜度也差
不多。skiplist的優勢是:a、skiplist實現簡單,容易控制。平衡樹增刪查改遍歷都更復雜。
b、skiplist的額外空間消耗更低。平衡樹節點存儲每個值有三叉鏈,平衡因子/顏色等消耗。
skiplist中p=1/2時,每個節點所包含的平均指針數目為2;skiplist中p=1/4時,每個節點所包
含的平均指針數目為1.33;
2. skiplist相比哈希表而言,就沒有那么大的優勢了。相比而言a、哈希表平均時間復雜度是
O(1),比skiplist快。b、哈希表空間消耗略多一點。skiplist優勢如下:a、遍歷數據有序
b、skiplist空間消耗略小一點,哈希表存在鏈接指針和表空間消耗。c、哈希表擴容有性能損
耗。d、哈希表再極端場景下哈希沖突高,效率下降厲害,需要紅黑樹補足接力。

 霍爾有感運行)



)


![[計算機畢業設計]基于深度學習的噪聲過濾音頻優化系統研究](http://pic.xiahunao.cn/[計算機畢業設計]基于深度學習的噪聲過濾音頻優化系統研究)






)


)
