C語言數據結構——詳細講解《二叉樹與堆的基本概念》
- 前言
- 一、樹的基礎概念
- 1.1 為什么需要樹?
- 1.2 樹的定義與結構
- 1.3 樹的核心術語
- 1.3 樹的核心術語
- 1.4 樹的表示方法(孩子兄弟表示法)
- 結構定義
- 為什么用孩子兄弟表示法?
- 1.5 樹的實際應用場景
- 二、二叉樹的概念與特性
- 2.1 為什么重點研究二叉樹?
- 2.2 二叉樹的定義與核心特點
- 2.3 特殊的二叉樹
- 2.3.1 滿二叉樹
- 2.3.2 完全二叉樹
- 2.4 二叉樹的重要性質
- 三、二叉樹的存儲結構
- 3.1 順序存儲(數組存儲)
- 原理
- 示例(完全二叉樹的順序存儲)
- 3.2 鏈式存儲(二叉鏈)
- 原理
- 結構定義(C語言)
- 示例(二叉鏈結構)
- 四、堆的概念與基礎實現
- 4.1 堆是什么?
- 4.2 堆的定義與核心條件
- 4.3 堆的存儲(數組順序存儲)
- 示例1:大根堆的數組存儲
- 示例2:小根堆的數組存儲
前言
- 在上一篇博客中,我們探討了隊列這種線性數據結構,而此前學習的棧也屬于線性結構——它們的元素都遵循“一對一”的線性邏輯關系。但在實際場景中,很多數據需要“一對多”的層級關系描述(比如文件系統、部門組織架構),此時線性結構就顯得力不從心。
- 今天,我們將進入非線性數據結構的世界,從最基礎的“樹”入手,逐步聚焦到應用最廣泛的“二叉樹”,最終講解一種特殊的二叉樹——“堆”。這三者層層遞進,是后續學習高級數據結構(如紅黑樹、B+樹)的核心基礎。
我的個人主頁,歡迎來閱讀我的其他文章
https://blog.csdn.net/2402_83322742?spm=1011.2415.3001.5343
我的C語言數據結構專欄
歡迎來閱讀指出不足
https://blog.csdn.net/2402_83322742/category_12830540.html?spm=1001.2014.3001.5482
一、樹的基礎概念
在學習二叉樹前,我們必須先理解“樹”的本質——它是所有層級結構數據的“通用模型”,而二叉樹是樹的“簡化版”。
1.1 為什么需要樹?
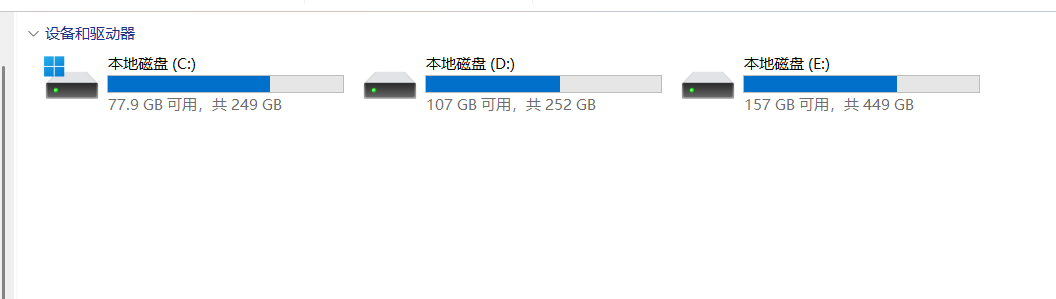
假設我們要存儲“電腦文件系統”的結構:C盤下有用戶和系統兩個文件夾,用戶下又有文檔和圖片……

- 如果用數組或鏈表(線性結構)存儲,只能按“C盤→用戶→文檔→圖片→系統”的順序排列,無法體現“父子文件夾”的層級關系。而樹的“一對多”結構,恰好能完美描述這種層級邏輯。
| 樹的核心價值:解決“層級數據”的存儲與訪問問題,彌補線性結構在“一對多”關系中的不足。 |
1.2 樹的定義與結構
樹是由n(n≥0)個有限結點組成的具有層次關系的集合,滿足以下規則:
- 有且僅有一個根結點(如文件系統的“C盤”),根結點沒有前驅結點;
- 除根結點外,其余結點被分成
m(m>0)個互不相交的子集(如“用戶”“系統”文件夾),每個子集都是一棵獨立的“子樹”; - 子樹之間不能相交(否則就變成了“圖”,而非樹);
- 一棵有
N個結點的樹,必有N-1條邊(每個結點除根外,都只通過一條邊連接父結點)。

1.3 樹的核心術語
樹的術語較多,下面我們詳細講解一下
1.3 樹的核心術語
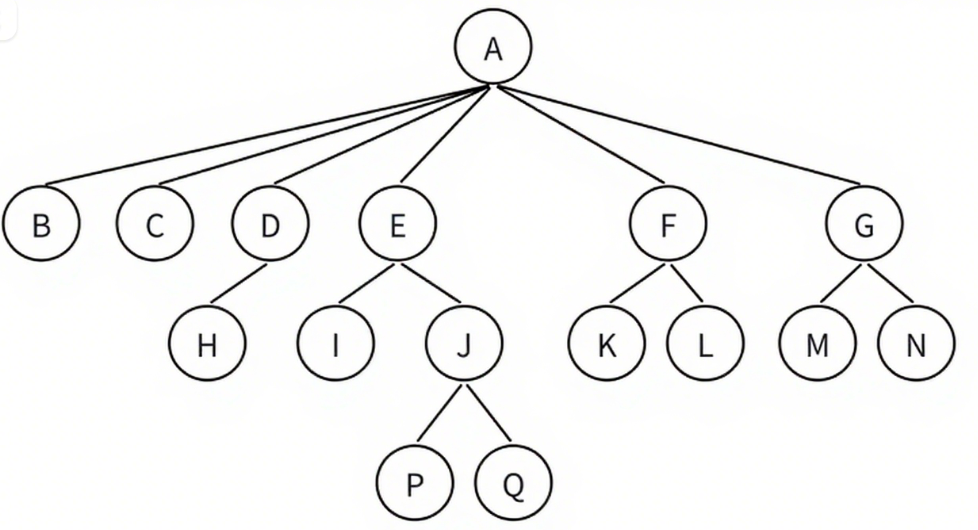
樹的術語較多,且需結合具體結構理解,我們以圖示的樹(根為A,子節點包含B、C、D、E、F、G等)為例,詳細講解:
| 術語 | 定義 | 示例(基于圖示樹) |
|---|---|---|
| 父結點/雙親 | 含有直接子結點的結點,是子結點的直接上層結點 | A是B、C、D、E、F、G的父結點(A直接包含這6個子結點) |
| 子結點/孩子 | 被父結點直接包含的結點,是父結點的直接下層結點 | B、C、D、E、F、G是A的子結點 |
| 結點的度 | 結點擁有的直接子結點數量(僅統計 immediate child) | A的度為6(有B、C、D、E、F、G共6個直接子結點) |
| 樹的度 | 樹中所有結點的度的最大值 | 樹的度為6(A的度最大,為6) |
| 葉子結點 | 度為0的結點(無任何直接子結點,是樹的“最底層終端結點”) | B、C、H、K、L、M、N、P、Q(這些結點沒有子結點) |
| 分支結點 | 度不為0的結點(非葉子結點,可繼續延伸子樹) | A、D、E、F、G、J(這些結點有直接子結點) |
| 兄弟結點 | 擁有相同父結點的結點 | B、C、D、E、F、G互為兄弟結點(它們的父結點都是A) |
| 結點的層次 | 從根開始計數,根為第1層,子結點為第2層,依此類推 | A在第1層;B、C在第2層;H、I在第3層;P、Q在第4層 |
| 樹的高度/深度 | 樹中結點的最大層次(從根到最底層葉子的最長路徑的層數) | 樹的高度為4(最底層結點P、Q在第4層) |
| 祖先 | 從根結點到該結點的路徑上的所有結點 | P的祖先是A、E、J(路徑:A→E→J→P) |
| 子孫 | 以該結點為根的子樹中的所有結點(包括間接子結點) | E的子孫是I、J、P、Q(E的子樹包含這些結點) |
| 森林 | m(m>0)棵互不相交的樹的集合(多棵獨立樹的組合) | 若“以B為根的樹”和“以C為根的樹”相互獨立,則它們組成森林 |
1.4 樹的表示方法(孩子兄弟表示法)
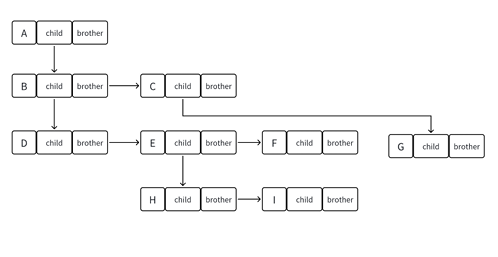
樹的存儲需要同時保存“結點值”和“結點間的層次關系”,常用的是孩子兄弟表示法
結構定義
// 樹的孩子兄弟表示法結點結構
typedef struct TreeNode {int data; // 結點存儲的數據struct TreeNode* firstChild; // 指向該結點的“第一個子結點”(左起第一個)struct TreeNode* nextBrother; // 指向該結點的“下一個兄弟結點”(同一父結點的右側兄弟)
} TreeNode;
為什么用孩子兄弟表示法?
- 優點:只需兩個指針(
firstChild和nextBrother),就能表示任意結構的樹;且能將樹“轉化為二叉樹”(把“兄弟關系”當作二叉樹的“右子樹”),后續可復用二叉樹的操作邏輯。 - 示例:若結點B有子結點E、F,且B的兄弟是C,則
B->firstChild = E,E->nextBrother = F,B->nextBrother = C。
1.5 樹的實際應用場景
- 文件系統:根目錄(根結點)→ 文件夾(分支結點)→ 文件(葉子結點);
- 組織架構:CEO(根結點)→ 部門總監(分支結點)→ 員工(葉子結點);
- 數據庫索引:B樹、B+樹(基于樹結構實現高效查詢)。
二、二叉樹的概念與特性
樹的結構靈活但復雜,而二叉樹是樹中最簡單、最常用的類型——它限制了結點的度不超過2,大大降低了操作難度,且任意樹都能轉換為二叉樹。
2.1 為什么重點研究二叉樹?
既然樹能表示任意層級關系,為什么還要專門學二叉樹?答案是**“trade-off(權衡)”**:
- 樹的結點度可以是任意值(如一個結點有100個子結點),導致操作邏輯(如遍歷、插入)非常復雜;
- 二叉樹限制“結點度≤2”,且子樹有“左、右之分”(有序),操作邏輯統一,易于實現;
- 關鍵:任意樹都能通過“孩子兄弟表示法”轉換為二叉樹,學會二叉樹就相當于掌握了所有樹的核心操作。
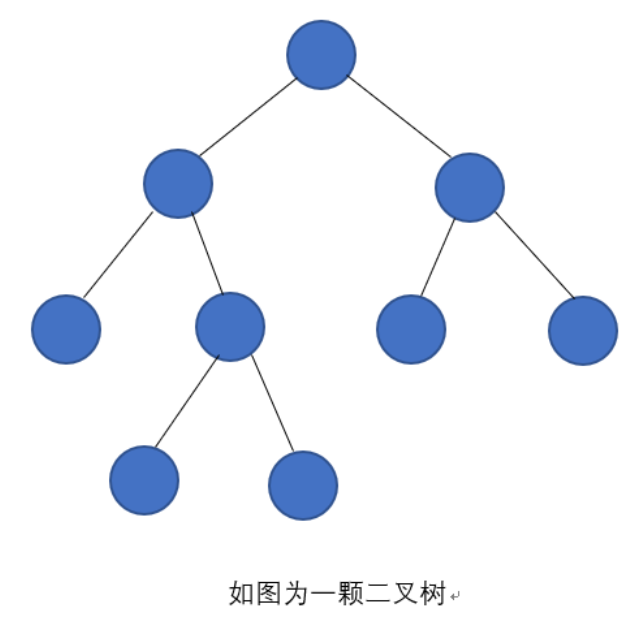
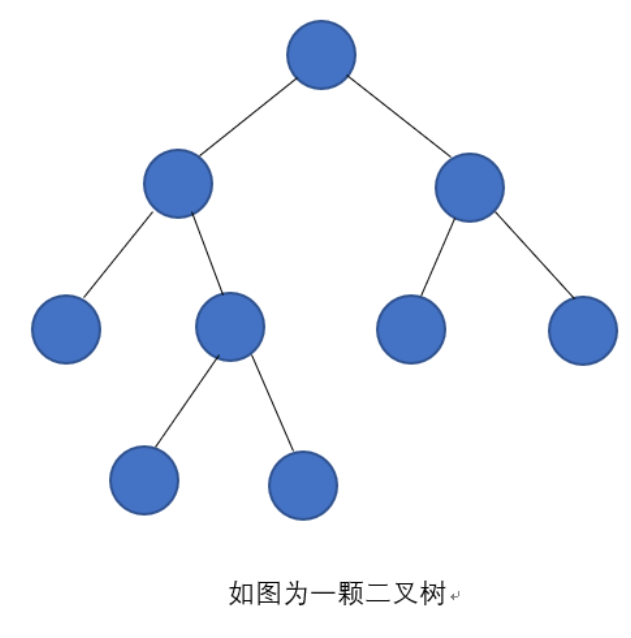
2.2 二叉樹的定義與核心特點
二叉樹是結點的有限集合,滿足:
- 集合為空(空二叉樹);
- 由一個根結點 + 一棵“左子樹” + 一棵“右子樹”組成,且左、右子樹均為二叉樹;
- 核心約束:
- 結點的度≤2(最多有2個孩子:左孩子、右孩子);
- 子樹有“左右次序”(左子樹和右子樹顛倒后,是不同的二叉樹)。
2.3 特殊的二叉樹
二叉樹中最常用的兩種特殊類型是“滿二叉樹”和“完全二叉樹”,后者是堆的基礎。
2.3.1 滿二叉樹
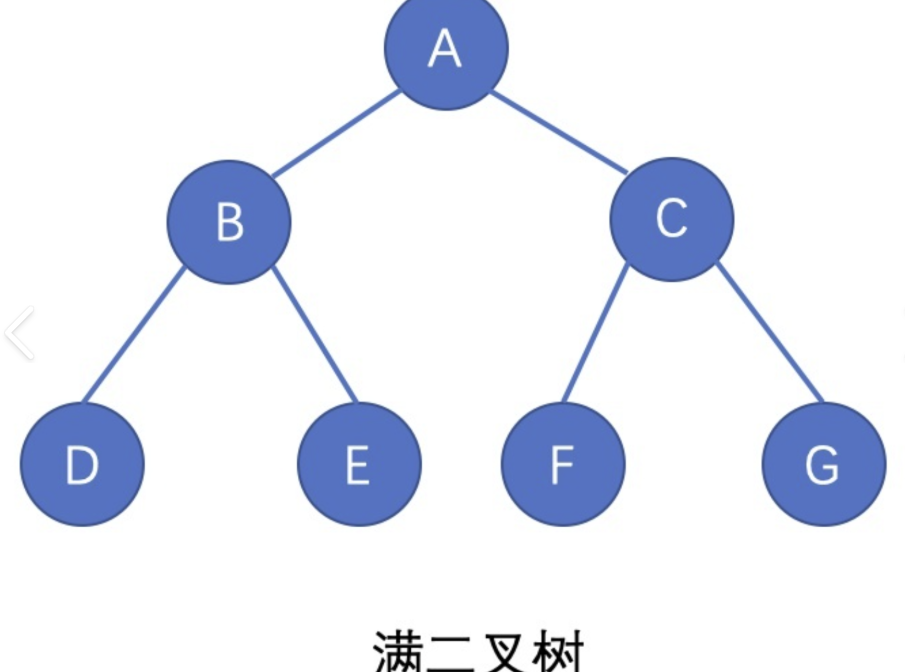
- 定義:每一層的結點數都達到最大值的二叉樹(即第k層有2^(k-1)個結點)。
- 公式:若滿二叉樹的層數為h,則總結點數為
2^h - 1(等比數列求和:1+2+4+…+2^(h-1) = 2^h -1)。 - 示例:h=3的滿二叉樹,總結點數=2^3 -1=7(第1層1個,第2層2個,第3層4個)。
2.3.2 完全二叉樹
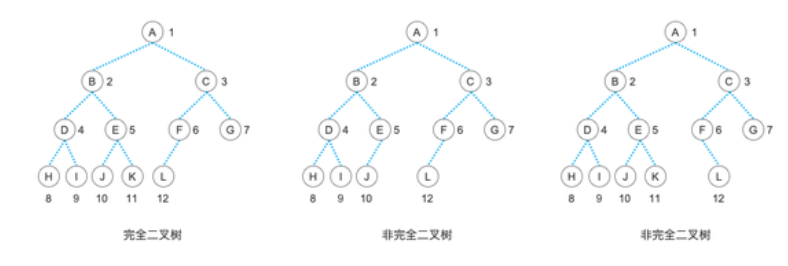
- 定義:深度為h、有n個結點的二叉樹,若其結點與“深度為h的滿二叉樹”中編號1~n的結點一一對應(編號從根開始,從上到下、從左到右),則為完全二叉樹。
- 核心特點:
- 葉子結點只能出現在最后兩層;
- 最后一層的葉子結點必須從左到右連續排列(不能有“左邊空、右邊有”的情況);
- 滿二叉樹是“特殊的完全二叉樹”(n=2^h -1時,完全二叉樹就是滿二叉樹)。
| 關鍵區別:滿二叉樹要求“每一層都滿”,完全二叉樹只要求“最后一層左連續”——完全二叉樹更靈活,且適合用數組存儲(無空間浪費)。 |
2.4 二叉樹的重要性質
以下性質基于“根結點層數為1”的規則,是后續堆操作的數學基礎:
- 第i層最多結點數:若根為第1層,則第i層最多有
2^(i-1)個結點(如第1層1=2^0 ,第2層2=2^1, 第3層4=2^2); - 深度h的最大結點數:深度為h的二叉樹,最多有
2^h -1個結點(即滿二叉樹的結點數公式); - 葉子結點與分支結點關系:對任意非空二叉樹,若葉子結點數為n0,度為2的結點數為n2,則必有
n0 = n2 + 1(推導:總邊數=總結點數-1,且邊數= n11 + n22,總結點數= n0 + n1 + n2,聯立得n0 = n2 +1); - 完全二叉樹的父/子索引關系:若完全二叉樹用數組存儲(索引從0開始),則序號為i的結點:
- 父結點序號:
(i-1)/2(整數除法,如i=1的父結點是0,i=2的父結點是0); - 左孩子序號:
2*i + 1(若2*i+1 < 總結點數,則存在左孩子); - 右孩子序號:
2*i + 2(若2*i+2 < 總結點數,則存在右孩子)。
- 父結點序號:
三、二叉樹的存儲結構
二叉樹有兩種存儲方式,分別對應不同的應用場景:
3.1 順序存儲(數組存儲)
原理
用數組存儲二叉樹的結點,結點的位置(索引)由其在完全二叉樹中的編號決定(參考“完全二叉樹的父/子索引關系”)。
- 適合場景:完全二叉樹(無空間浪費);
- 不適合場景:非完全二叉樹(空結點需占用數組位置,空間利用率低)。
示例(完全二叉樹的順序存儲)
若完全二叉樹結點為[A, B, C, D, E, F](根為A,左子樹B、D、E,右子樹C、F),數組存儲如下:
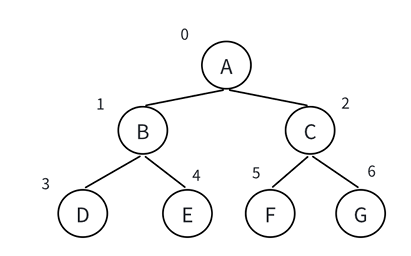
| 數組索引 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 結點值 | A | B | C | D | E | F |
- A(0)的左孩子是B(1=20+1),右孩子是C(2=20+2);
- B(1)的左孩子是D(3=21+1),右孩子是E(4=21+2);
- C(2)的左孩子是F(5=22+1),右孩子不存在(22+2=6 ≥ 總結點數6)。
3.2 鏈式存儲(二叉鏈)
原理
用鏈表存儲二叉樹,每個結點包含“數據域”和兩個“指針域”(分別指向左孩子和右孩子),稱為“二叉鏈”。
- 適合場景:所有二叉樹(尤其是非完全二叉樹,無空間浪費,靈活);
- 缺點:無法像數組那樣隨機訪問,需通過指針遍歷。
結構定義(C語言)
// 二叉樹的鏈式存儲(二叉鏈)
typedef struct BinaryTreeNode {int data; // 結點數據struct BinaryTreeNode* leftChild; // 指向左孩子的指針struct BinaryTreeNode* rightChild; // 指向右孩子的指針
} BTNode;
示例(二叉鏈結構)
對于結點[A, B, C, D](A的左是B,右是C;B的左是D),二叉鏈的結構為:
A
├─ leftChild → B
│ ├─ leftChild → D
│ └─ rightChild → NULL
└─ rightChild → C├─ leftChild → NULL└─ rightChild → NULL
四、堆的概念與基礎實現
堆是特殊的完全二叉樹,也是二叉樹順序存儲的典型應用(如優先隊列、堆排序)
4.1 堆是什么?
我們已經有了完全二叉樹,為什么還要定義“堆”?因為堆在“快速獲取最大值/最小值”場景中效率極高——堆的根結點永遠是“最大值(大堆)”或“最小值(小堆)”,無需遍歷整個樹就能獲取極值。
4.2 堆的定義與核心條件
堆是滿足以下兩個條件的完全二叉樹:
- 結構條件:堆必須是一棵完全二叉樹(保證可以用數組順序存儲,無空間浪費);
- 值條件(堆序性):
- 大堆:每個父結點的值 ≥ 其左右子結點的值(根是最大值);
- 小堆:每個父結點的值 ≤ 其左右子結點的值(根是最小值)。
4.3 堆的存儲(數組順序存儲)
堆是完全二叉樹,因此用數組存儲最高效(無需額外指針,僅通過索引即可推導父子關系)。存儲規則與完全二叉樹一致,核心依賴“父、左孩子、右孩子的索引推導”:
- 數組索引從
0開始; - 對于序號為
i的結點,可通過公式快速找到其親屬結點:- 父結點索引:
(i - 1) / 2(整數除法,向下取整); - 左孩子索引:
2 * i + 1(若計算結果< 堆的元素個數,則左孩子存在); - 右孩子索引:
2 * i + 2(若計算結果< 堆的元素個數,則右孩子存在)。
- 父結點索引:
示例1:大根堆的數組存儲
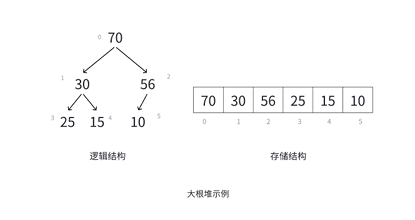
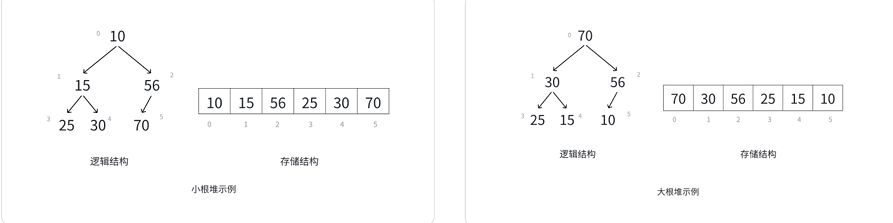
大根堆的邏輯結構:根結點為70,左子結點30,右子結點56;30的左子結點25、右子結點15;56的右子結點10。
其數組存儲結構為 [70, 30, 56, 25, 15, 10](數組索引0~5對應元素),各結點的親屬關系推導如下:
| 數組索引 | 結點值 | 父結點(索引/值) | 左孩子(索引/值) | 右孩子(索引/值) |
|---|---|---|---|---|
| 0 | 70 | 無(根結點) | 2*0+1=1 / 30 | 2*0+2=2 / 56 |
| 1 | 30 | (1-1)/2=0 / 70 | 2*1+1=3 / 25 | 2*1+2=4 / 15 |
| 2 | 56 | (2-1)/2=0 / 70 | 2*2+1=5 / 10 | 無(2*2+2=6 ≥ 元素個數6) |
| 3 | 25 | (3-1)/2=1 / 30 | 無(2*3+1=7 ≥ 6) | 無(2*3+2=8 ≥ 6) |
| 4 | 15 | (4-1)/2=1 / 30 | 無(2*4+1=9 ≥ 6) | 無(2*4+2=10 ≥ 6) |
| 5 | 10 | (5-1)/2=2 / 56 | 無(2*5+1=11 ≥ 6) | 無(2*5+2=12 ≥ 6) |
示例2:小根堆的數組存儲
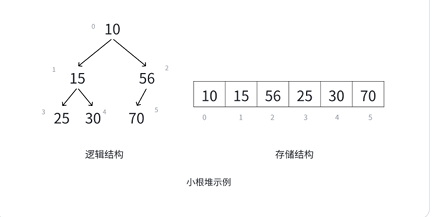
小根堆的邏輯結構:根結點為10,左子結點15,右子結點56;15的左子結點25、右子結點30;56的右子結點70。
其數組存儲結構為 [10, 15, 56, 25, 30, 70](數組索引0~5對應元素),親屬關系推導更能體現“小根堆父結點≤子結點”的特性:
| 數組索引 | 結點值 | 父結點(索引/值) | 左孩子(索引/值) | 右孩子(索引/值) |
|---|---|---|---|---|
| 0 | 10 | 無(根結點) | 2*0+1=1 / 15 | 2*0+2=2 / 56 |
| 1 | 15 | (1-1)/2=0 / 10 | 2*1+1=3 / 25 | 2*1+2=4 / 30 |
| 2 | 56 | (2-1)/2=0 / 10 | 2*2+1=5 / 70 | 無(2*2+2=6 ≥ 6) |
| 3 | 25 | (3-1)/2=1 / 15 | 無(2*3+1=7 ≥ 6) | 無(2*3+2=8 ≥ 6) |
| 4 | 30 | (4-1)/2=1 / 15 | 無(2*4+1=9 ≥ 6) | 無(2*4+2=10 ≥ 6) |
| 5 | 70 | (5-1)/2=2 / 56 | 無(2*5+1=11 ≥ 6) | 無(2*5+2=12 ≥ 6) |
我的個人主頁,歡迎來閱讀我的其他文章
https://blog.csdn.net/2402_83322742?spm=1011.2415.3001.5343
我的C語言數據結構專欄
歡迎來閱讀指出不足
https://blog.csdn.net/2402_83322742/category_12830540.html?spm=1001.2014.3001.5482
| 非常感謝您的閱讀,喜歡的話記得三連哦 |





)
)




![[光學原理與應用-417]:非線性光學 - 線性光學(不引發頻率的變化)與非線性光學(引發頻率變化)的異同](http://pic.xiahunao.cn/[光學原理與應用-417]:非線性光學 - 線性光學(不引發頻率的變化)與非線性光學(引發頻率變化)的異同)

![[linux倉庫]性能加速的隱形引擎:深度解析Linux文件IO中的緩沖區奧秘](http://pic.xiahunao.cn/[linux倉庫]性能加速的隱形引擎:深度解析Linux文件IO中的緩沖區奧秘)




)

