目錄

一：題目鏈接

二：題目思路

三：代碼實現

---

一：題目鏈接

? ? ? ? 題目的要求是找出當前數組能組成三角形三元組的個數。

二：題目思路

? ? ? ? 有一種暴力枚舉解法，利用三層 for 循環來一一枚舉三元組的情況，如圖：

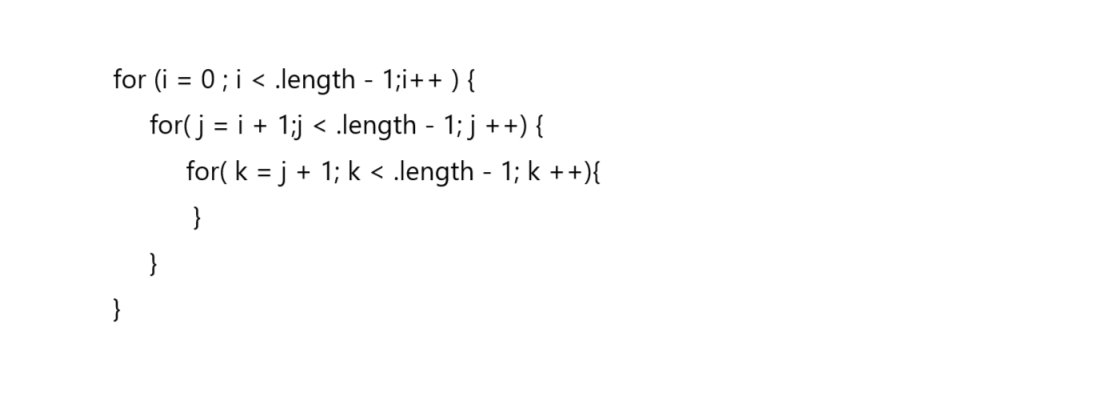
這種解法的時間復雜度已經達到 o(n^3) ，會超時，這不是最優的解法。

? ? ? ? 有另一種解法，利用數組的單調性配合雙指針的算法思想。

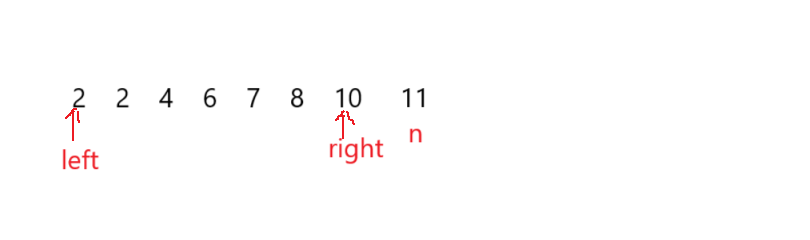
? ? ? ? 首先，先把數組從小到大排個序，然后，先固定該數組中最大的元素（如上圖中的 n ），定義兩個指針，一個指向數組起始下標，另一個指向該數組中最大的元素上一位的下標，現在有兩種情況。

????????如果當前的 left 和 right 的元素加起來比 n 大，證明該組合的三元組是可以構建三角形的，并且也側向說明 如果 left 往右邊遍歷數組再和 right（不動）下標元素加起來也肯定 比 n 大，所以，期間的這種情況有 right - left 種，就不需要一次次遍歷判斷了，再 right--，進入下一次判斷。

????????如果?當前的 left 和 right 的元素加起來比 n 小，證明該組合的三元組不能構建三角形，并且也側向說明 如果 right 往左邊遍歷數組再和 left（不動）下標元素加起來也肯定 比 n 小，就不需要一次次遍歷判斷了，直接 left++，進入下一次判斷。

? ? ? ? 以上這樣，我們就完成了一個當前數組最大的數的判斷，以此不斷往上循環這個過程。

三：代碼實現

     //排序數組Arrays.sort(nums);//計數器int sum = 0;//先固定最大的數for(int i = nums.length - 1;i > 1;i--) {int left = 0;int right = i - 1;while(left < right) {if(nums[left] + nums[right] > nums[i]) {sum += right - left;right--;}else {left++;}}}return sum;