一、概念理解

“機器學習對于高值的預測保守”，這是建模里很常見的現象，尤其在生態、氣候、遙感這類數據分布高度偏斜的場景。

通常可以從以下幾個角度理解：

1. 數據分布與樣本稀缺

在訓練集里，高值樣本往往非常少，遠低于中低值的占比。機器學習模型在最小化總體誤差時，會更傾向于“貼合”多數樣本的中低區間，從而導致對高值的預測趨向于低估。

2. 損失函數的作用

常見的損失函數（如 MSE、MAE）本質上是對“平均誤差”的優化，高值樣本雖然誤差可能很大，但數量太少，整體在損失中的權重有限，模型就會“犧牲”這些極端點以換取整體精度。

3. 模型的正則化與泛化傾向

像 CatBoost、XGBoost 或 Random Forest 這類集成模型，會通過葉子數、深度限制、學習率衰減等方式防止過擬合。這種“保守”的機制在高值預測上會顯得更明顯：因為高值點往往是噪聲或異常值的來源，模型寧可收縮預測值，也不愿意強行拉到很高。

4. 特征空間覆蓋不足

高值樣本可能對應特殊的環境條件或特征組合，但訓練數據里這類情況出現很少。模型在這類區域缺乏學習支撐，只能在已有趨勢上外推，結果就是“回歸到均值”式的保守預測。

常見的解決思路包括：
（1）樣本再平衡（過采樣高值、欠采樣中低值）；
（2）改變損失函數（如加權MSE、Quantile Loss、Huber Loss）；
（3）特征工程增強（加入更能解釋高值的變量）；
（4）后處理（如殘差建模、分段建模）。

---

二、殘差建模嵌入

1. 基本思路

第一次模型（主模型）已經捕捉了數據的主要趨勢，但在高值區間往往出現系統性低估。此時我們可以：

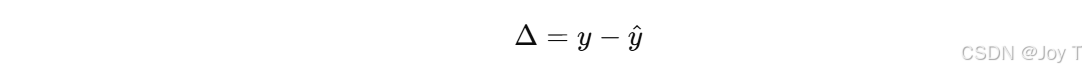
把殘差 Δ當作新的目標變量，用原始特征 X 或者新構造的特征 X′ 去訓練一個“殘差模型”。

最終預測時，把主模型和殘差模型的輸出疊加：

---

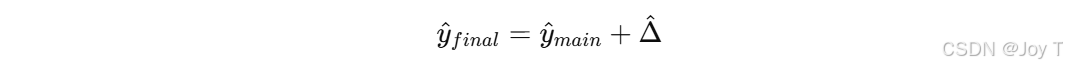
2. 為什么對高值有效

（1）殘差在高值區間往往帶有系統性偏差（總是負的，表示低估），殘差建模能單獨學習這種規律。
（2）主模型負責整體趨勢，殘差模型負責修正極端值，分工明確，能提高高值段的擬合能力。
（3）相比直接讓主模型去“硬擬合”高值，殘差建模更穩定，因為它把任務拆解成“趨勢 + 偏差”兩部分。

---

3. 與“Δ變化”分析的關系

你提到的“對 Δ 的變化進行擬合分析”正是殘差建模的核心。更進一步，可以：
（1）畫殘差 vs 特征的散點，看看在哪些特征區間高估/低估明顯；
（2）如果殘差和某些變量（比如林分密度、降雨量、溫度）高度相關，就說明主模型在這類變量的高值/極端情況下表現不足；
（3）殘差模型就可以重點利用這些變量來修正。【發現問題，修正問題】

---

4. 延伸做法

（1）Boosting 系列模型（XGBoost、CatBoost）其實就是多輪殘差建模的堆疊，只不過是每棵樹擬合殘差的增量。
（2）在碳儲量、碳通量建模里，可以嘗試“主模型 + 生態學啟發殘差模型”，例如先用 CatBoost 做趨勢，再用一個小型回歸模型專門擬合高值殘差。
（3）如果想要“保守預測高值但同時捕捉區間”，還可以考慮 分位數回歸（Quantile Regression），結合殘差建模一起使用。

---

三、損失函數更新

常見的 MSE/MAE 損失函數確實會讓模型趨向于“均值回歸”，從而在高值區間預測偏保守。要解決這個問題，可以考慮以下幾類與“極端值/不對稱誤差”相關的損失函數，它們能夠讓模型更關注高值樣本：

---

1. 分位數損失（Quantile Loss）

機制：不是擬合均值，而是擬合某個分位數（比如 0.9 分位），這樣輸出會有意識地“抬高”，適合不想低估高值的情況。

---

2. 加權損失（Weighted Loss）

機制：對高值樣本加權，使其在損失函數里比低值樣本更重要。

---

3. Huber Loss / Smooth L1 Loss

• 機制：在誤差小的時候近似 MAE，在誤差大時近似 MSE，能緩解極端值對整體的沖擊，但它更多是穩健化，而不是專門提高高值的預測。

• 適用場景：如果你擔心高值既可能是“真值”也可能是“噪聲”，Huber 比較穩妥。

---

4. 極端值敏感損失（Tail-sensitive Loss）

• 機制：在金融、氣象等領域，有些研究會引入對尾部殘差特別敏感的損失函數，比如 GEV（廣義極值分布）似然、或基于 log(1+error2) 的函數。

• 作用：能讓模型顯式地在高值區間花更多注意力。

---

簡單來說，如果你的目標是讓模型敢于預測更高的值：
（1）首選分位數損失（Quantile Loss） —— 控制預測落在分布高端；
（2）其次是加權損失（Weighted MSE/MAE） —— 強調高值樣本的重要性；
（3）再配合殘差建模 —— 對高值區間的系統性低估進行二次修正。