一、題目

介紹：漢諾塔（Tower of Hanoi），又稱河內塔，是一個源于印度古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。
游戲要求：
1、每次只能移動一個圓盤。
2、圓盤只能放置在比它大的圓盤上。
3、圓盤在新的柱子上也是從上到下、從小到大排列。

二、分析

假設n表示個圓盤個數，三根柱子分別用A，B，C進行表示，n個圓盤最初均放在A柱上，我們要將圓盤全部移到C柱上。

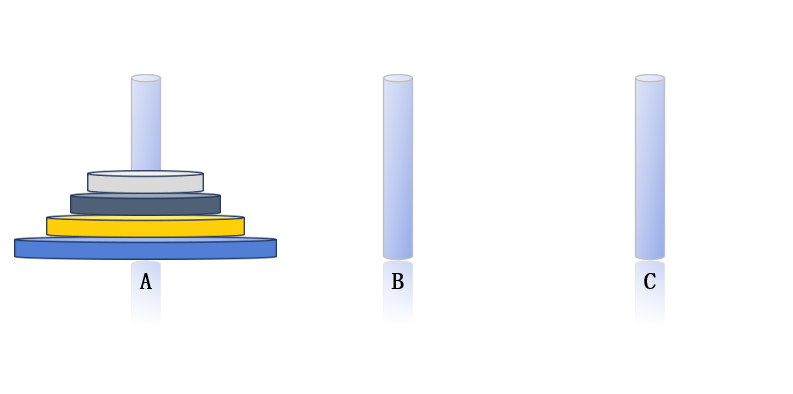
n = 1時，我們只需要1步就能將圓盤移動到C柱：A —> C

n = 2時，需要3步才能將圓盤移動到C柱：A —> B、A —> C、B —> C

n = 3時，需要7步才能將圓盤移動到C柱：A —> C、A —> B、C —> B、A —> C、B —> A、B —> C、A —> C

對于n個圓盤，我們可以參照3個盤子移動的情況，先將A柱上面的n - 1個圓盤通過C柱移動到B柱，剩下最大的那個圓盤直接移動到C柱，B柱上的圓盤通過A柱再移動到C柱上。其需要移動的次數為2^n-1次或者是n - 1個圓盤移動次數乘以2減1。（遞歸）



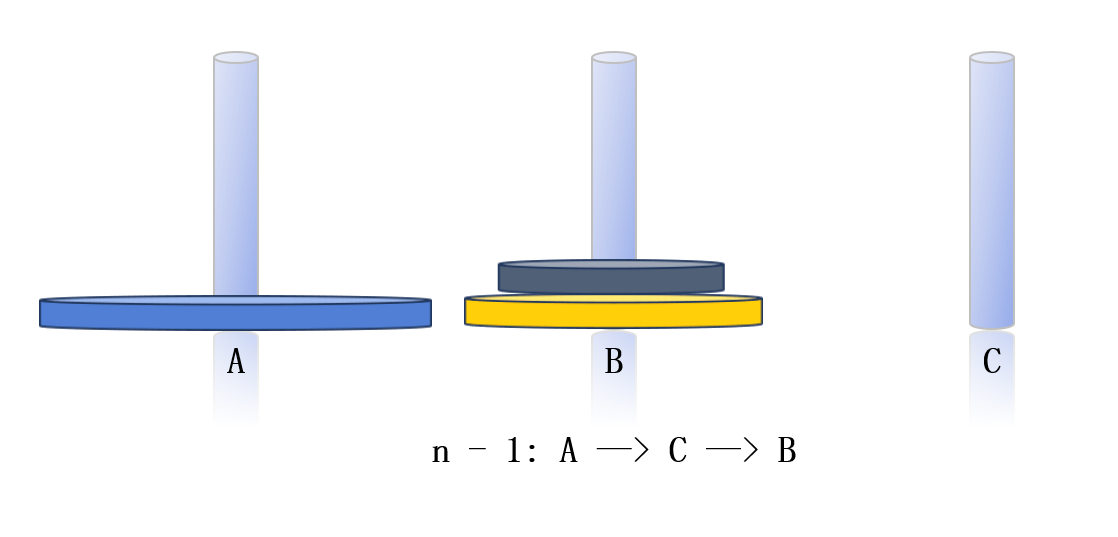
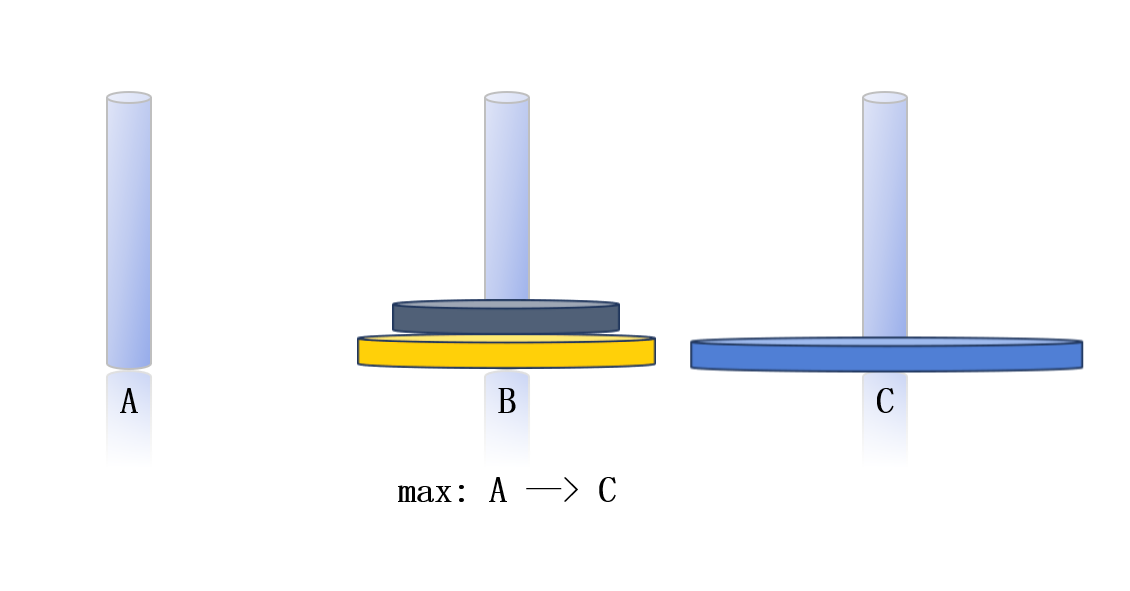
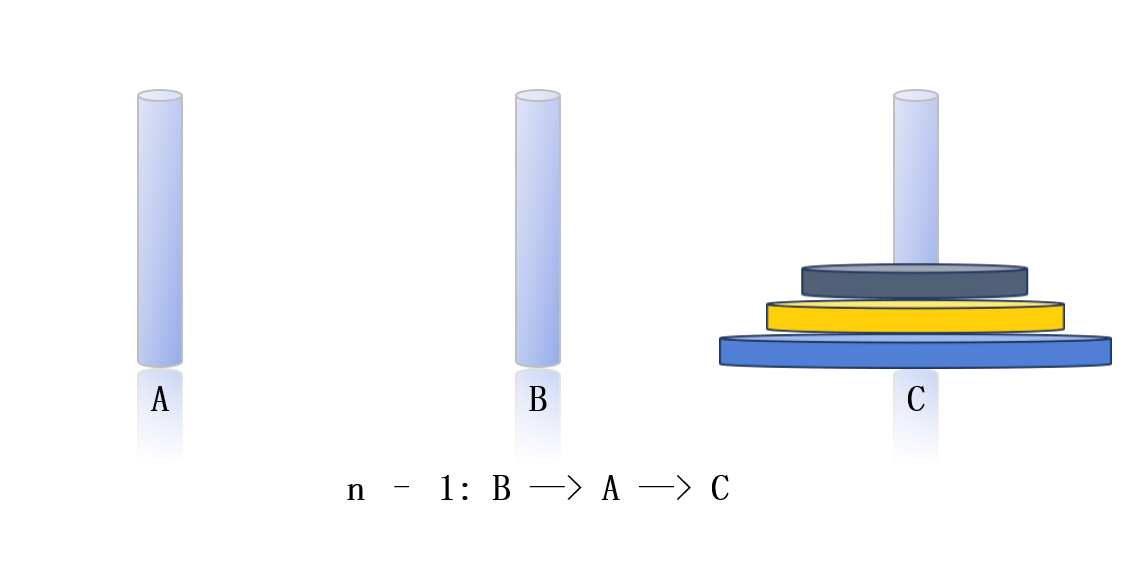
可以把問題看成是把大象塞進冰箱：①打開冰箱門；②把大象關進冰箱；③關上冰箱門

三、代碼實現

移動軌跡：

#include <stdio.h>void Move(char x, char y)
{printf("%c ——> %c ", x, y);//移動軌跡
}void Hanoi(int n, char A, char B, char C)
{	if(n ==1)Move(A, C);else{	Hanoi(n - 1, A, C, B);//上面n - 1個通過C柱移動到B柱Move(A, C);//底部最大圓盤直接移動到C柱Hanoi(n - 1, B, A, C);//n - 1個圓盤通過A柱移動到C柱}
}int main()
{int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');//n個圓盤從A柱挪到C柱return 0;
}

運行結果：

移動次數：

#include <stdio.h>int Hanoi(int n)
{if(n == 1)return 1;elsereturn 2 * Hanoi(n - 1) + 1;//移動次數是n - 1個圓盤移動次數乘2減1
}int main()
{int n = 0;scanf("%d", &n);int ret = Hanoi(n);printf("%d", ret);return 0;
}

運行結果：