hello大家好，今天是2025年8月23日，我要來給大家分享的是一個高階數據結構---ST表。

一：引入

1.RMQ問題：

對于一個長度為 n 的序列，有 m 次查詢操作，每次查詢為一個區間 [l，r] 的最大值（最小值）。

上述問題可以用線段樹來解決。但是殺雞焉用宰牛刀，對于這種靜態問題，我們可以使用代碼量更少的方式來解決------ST表。

2.ST表：

ST表（Sparse Table，稀疏表）是一種基于動態規劃和倍增思想實現的數據結構，形式上是一張二維表格。ST表通過預處理一些信息，從而快速處理區間查詢。（類似前綴和數組~）其中，預處理的時間復雜度為 O（n * log n），查詢操作為 O（1）。由于在查詢前需要預處理出一些信息，因此ST表基本上只能解決靜態問題。

ST表

將信息預處理完畢之后，對于查詢操作只需要在這張二維表格中拿值就可以了。

這里解釋一個名詞：靜態問題---以數組操作為例：

有靜態問題就會有動態問題，靜態問題就是只有查詢操作沒有修改操作，或者查詢操作是在所有修改操作全部結束之后進行。相比之下，動態問題就是修改操作和查詢操作交叉進行。

ST表能夠解決的問題（靜態問題）線段樹絕大多數都可以解決，線段樹能解決的問題（靜態問題 & 動態問題）ST表就不一定可以解決。

3.ST表維護的信息：

ST表維護的信息需要滿足結合律和可重復貢獻。（例如區間最值以及區間gcd）

這里借助一張圖解釋一下什么是結合律和可重復貢獻。

如果不滿足結合率和可重復貢獻，ST表就不能解決。例如區間和以及區間乘積。

二：ST表的實現

計算機中的 log 默認是下取整的，在這里提前說一下，下面就不過多贅述了。

1.ST表維護信息的方式：

對于一個長度為 n 的序列，有 m 次查詢操作，每次查詢為一個區間 [l，r] 的最大值。

由于區間最值不滿足可差性，因此不能像前綴和數組一樣搞一張一維表格來預處理某些區間的信息。由于二維表格可以直接用來表示區間，那么可以嘗試用二維的表格來預處理，一種直接的方式就是：f[i][j] 表示區間 [i, j] 的最值。

這種方式肯定是可以解決問題的。但是，RMQ 問題的數組一般都是 1e5~1e6 級別的長度，這張二維表格根本無法創建出來（空間溢出）。

我們嘗試使用倍增的思想??優化一下狀態表示:

f[i][j] 表示：從 i 位置開始，長度為??的區間中，所有元素的最值。

以數組 a = 【5，2，4，6，1，7，5，0，9，3】為例，我們會用下述方式維護區間最大值信息。

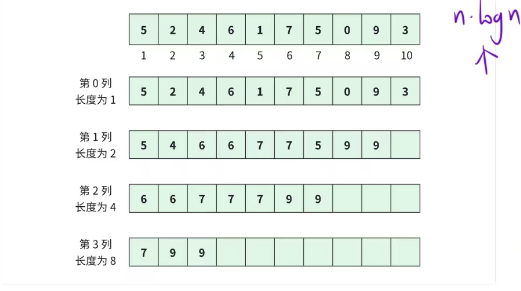
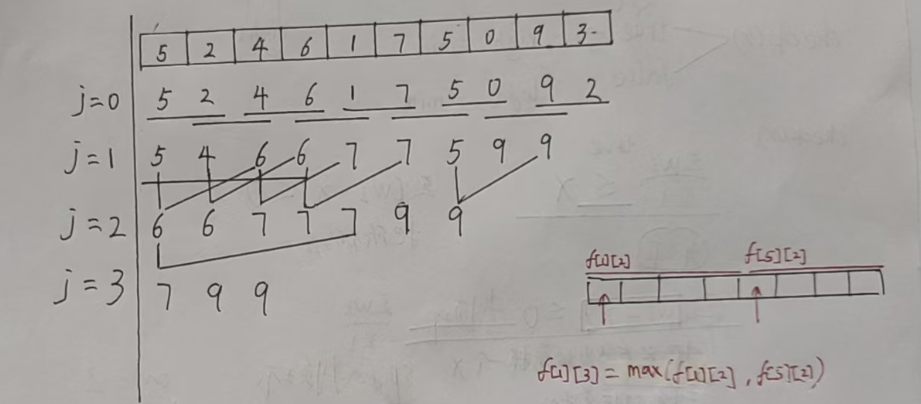
這就是稀疏表的由來，并不是把所有的區間信息存下來，只存長度為 2^j 的區間信息。

優化之后，第二維空間大小 n 只需保證 2^n >= N 就行。25~30就足夠了。可見，這個優化是非常有效的。

2.ST表的查詢

預處理工作結束之后，我們能否使用預處理出的信息快速查詢區間最值呢？

比如，我們要查詢區間【l，r】的最大值：

根據狀態表示，我們只需要先求出 k = log(2)(r - l + 1)（下取整），然后再從 f[l][k] 和

f[r - (1 << k) + 1][k] 兩個格子中取最大值即可。

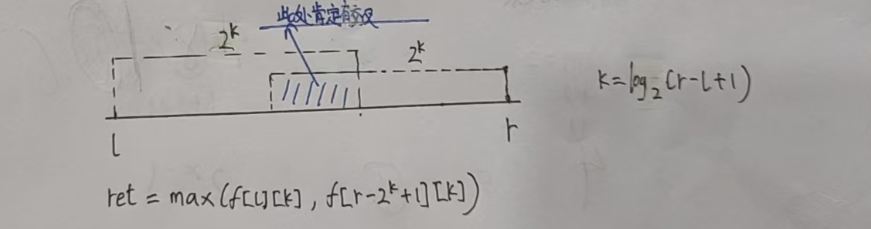
3.記憶區間起點和區間終點的技巧

• 起點 + 區間長度 = 下一個區間的起點。
• 終點?-? 區間長度 = 上一個區間的終點。

4.ST表的實現

初始化

#include <iostream>
#include <cmath>using namespace std;
const int N = 1e5 + 10;int n;
int a[N], f[N][25]; // j ^ 25 >= N 就行  void init()
{for(int i = 1; i <= n; i++) f[i][0] = a[i];for(int j = 1; j <= log2(n); j++)for(int i = 1; i + (1 << j) - 1 <= n; i++)f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}

查詢

int query(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k]);
}

5.優化log（看題目情況）

如果查詢次數過多，是會有一個 log 的開銷的。如果把 log1~logn 全部預處理出來，那么查詢操作的 k 就可以在 O（1）的時間得到。

對于對數運算，有如下公式：

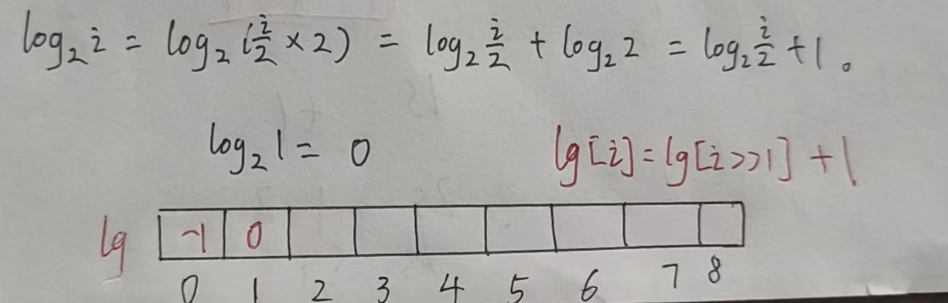
因此可以通過遞推，預處理出來所有的 log1 ~ logn。

加了優化的ST表：

#include <iostream>
#include <cmath>using namespace std;
const int N = 1e5 + 10;int n;
int a[N], f[N][25]; // j ^ 25 >= N 就行  
int lg[N];void init()
{lg[0] = -1; // 為了方便遞推 lg[1] = lg[0] + 1 == 0 for(int i = 1; i <= n; i++){lg[i] = lg[i >> 1] + 1;f[i][0] = a[i];} for(int j = 1; j <= lg[n]; j++)for(int i = 1; i + (1 << j) - 1 <= n; i++)f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}int query(int l, int r)
{int k = lg[r - l + 1];return max(f[l][k], f[r - (1 << k) + 1][k]);
}

三：ST表模板題

題目一：【模板】ST表 && RMQ 問題

題目鏈接：【模板】ST表 && RMQ 問題

#include <iostream>
#include <cmath>using namespace std;const int N = 1e5 + 10;int n, m;
int f[N][25];int RMQ(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) scanf("%d", &f[i][0]);//初始化for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; scanf("%d%d", &l, &r);printf("%d\n", RMQ(l, r));}return 0;
}

題目二：gcd 區間

題目鏈接：gcd 區間

#include <iostream>
#include <cmath>using namespace std;const int N = 1e3 + 10;int n, m;
int f[N][25];int gcd(int a, int b)
{return b == 0 ? a : gcd(b, a % b);
}int query(int l, int r)
{int k = log2(r - l + 1);return gcd(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++) cin >> f[i][0];for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = gcd(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; cin >> l >> r;cout << query(l, r) << endl;}return 0;
} 

四：ST表練習題

題目一：質量檢測

題目鏈接：質量檢測

這道題目的最優解是單調隊列 O（n），但是我們這個專題是 ST 表，因此給出ST表的解法，下去之后也要嘗試一下使用單調隊列解決這道問題。

#include <iostream>
#include <cmath>
#include <cstring>using namespace std;const int N = 1e5 + 10;int n, m;
int f[N][25];int query(int l, int r)
{int k = log2(r - l + 1);return min(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{memset(f, 0x3f, sizeof f);cin >> n >> m;for (int i = 1; i <= n; i++) cin >> f[i][0];for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}for (int i = 1; i + m - 1 <= n; i++){cout << query(i, i + m - 1) << endl;}return 0;
} 

題目二：Balanced Lineup G

題目鏈接：Balanced Lineup G

#include <iostream>
#include <cstring>
#include <cmath>using namespace std;const int N = 5e4 + 10;int n, m;
int f[N][28];
int g[N][28];int query(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k])- min(g[l][k], g[r - (1 << k) + 1][k]);
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);for (int i = 1; i <= n; i++){cin >> f[i][0];g[i][0] = f[i][0];}for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);g[i][j] = min(g[i][j - 1], g[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; cin >> l >> r;cout << query(l, r) << endl;}return 0;
}

今天的分享就到這里了~~，如果大家有疑問的話，歡迎下來之后和我溝通~~