前面我們學過了控制二叉搜索樹平衡的AVL樹，今天我們就來學習控制二叉搜索樹平衡的另一種—紅黑樹

1. 認識紅黑樹

• 紅黑樹（Red-Black Tree）是一種自平衡的二叉查找樹（BST），通過特定的規則和旋轉操作維持樹的平衡，從而保證高效的查找、插入和刪除操作。它的核心用途是在動態數據集中提供對數時間復雜度（O(logN)）的搜索、插入和刪除性能，尤其適用于需要頻繁修改且要求高效查詢的場景
• 紅黑樹是?棵二叉搜索樹，他的每個結點增加一個存儲位來表示結點的顏色，可以是紅色或者黑色。通過對任何一條從根到葉子的路徑上各個結點的顏色進行約束，紅黑樹確保沒有一條路徑會比其他路徑長出2倍，因而是接近平衡的

1.1 紅黑樹的規則

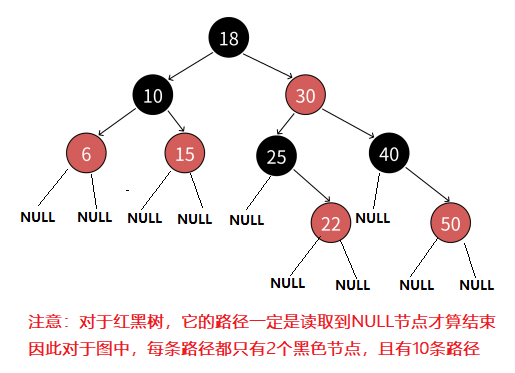
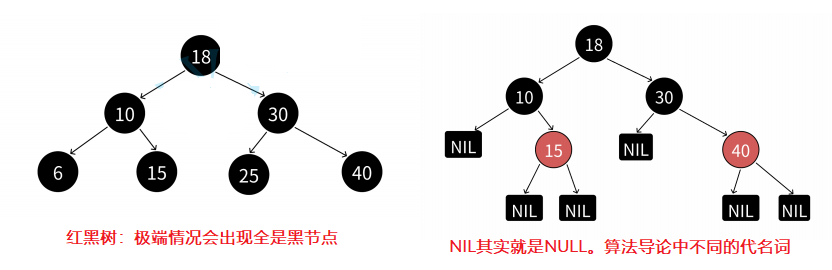
1. 每個節點不是紅色就是黑色
2. 根節點是黑色的
3. 如果一個節點是紅色的，那么它的兩個孩子節點必須是黑色的，也就是說任意一條路徑不會有連續的紅色節點
4. 對于任意一條路徑，從該節點到其所有NULL節點的簡單路徑上，均包含相同數量的黑色節點
   

---

---

1.2 紅黑樹如何確保最長路徑不超過最短路徑的2倍呢?

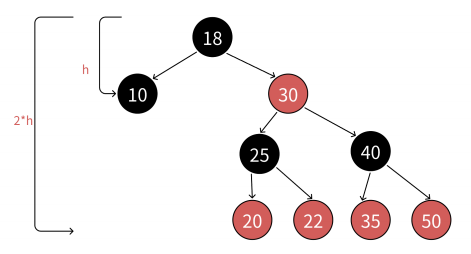
• 由規則4可知，從根到NULL結點的每條路徑都有相同數量的黑色結點，所以極端場景下，最短路徑就就是全是黑色結點的路徑，假設最短路徑長度為bh(black height)
• 由規則2和規則3可知，任意一條路徑不會有連續的紅色結點，所以極端場景下，最長的路徑就是一黑一紅間隔組成，那么最長路徑的長度為2*bh
• 綜合紅黑樹的4點規則而言，理論上的全黑最短路徑和一黑一紅的最長路徑并不是在每棵紅黑樹都存在的。假設任意一條從根到NULL結點路徑的長度為x，那么bh <= x <= 2*bh

1.3 紅黑樹的效率

---

• 假設N是紅黑樹樹中結點數量，h最短路徑的長度，那么 , 由此推出h ≈ logN，也就是意味著紅黑樹增刪查改最壞也就是走最長路徑 ，那么時間復雜度還是O(logN)
• 紅黑樹的表達相對AVL樹要抽象?些，AVL樹通過高度差直觀的控制了平衡。紅黑樹通過4條規則的顏色約束，間接的實現了近似平衡，他們效率都是同?檔次，但是相對而言，插入相同數量的節點，紅黑樹的旋轉次數是更少的，因為他對平衡的控制沒那么嚴格

• 最差全黑

---

2. 實現紅黑樹

2.1 紅黑樹的結構

---

2.2 紅黑樹的插入

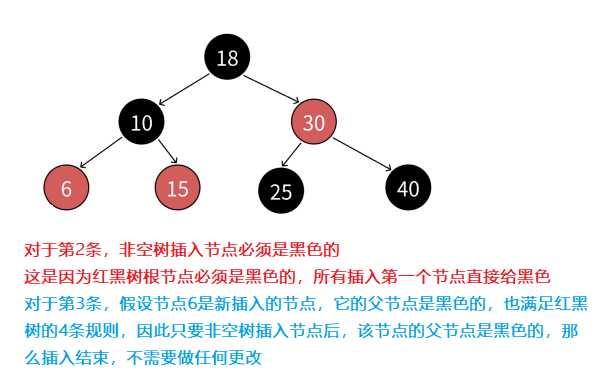
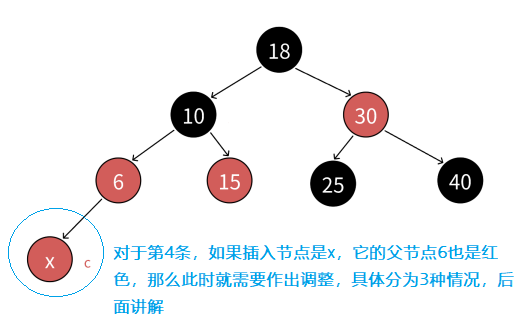
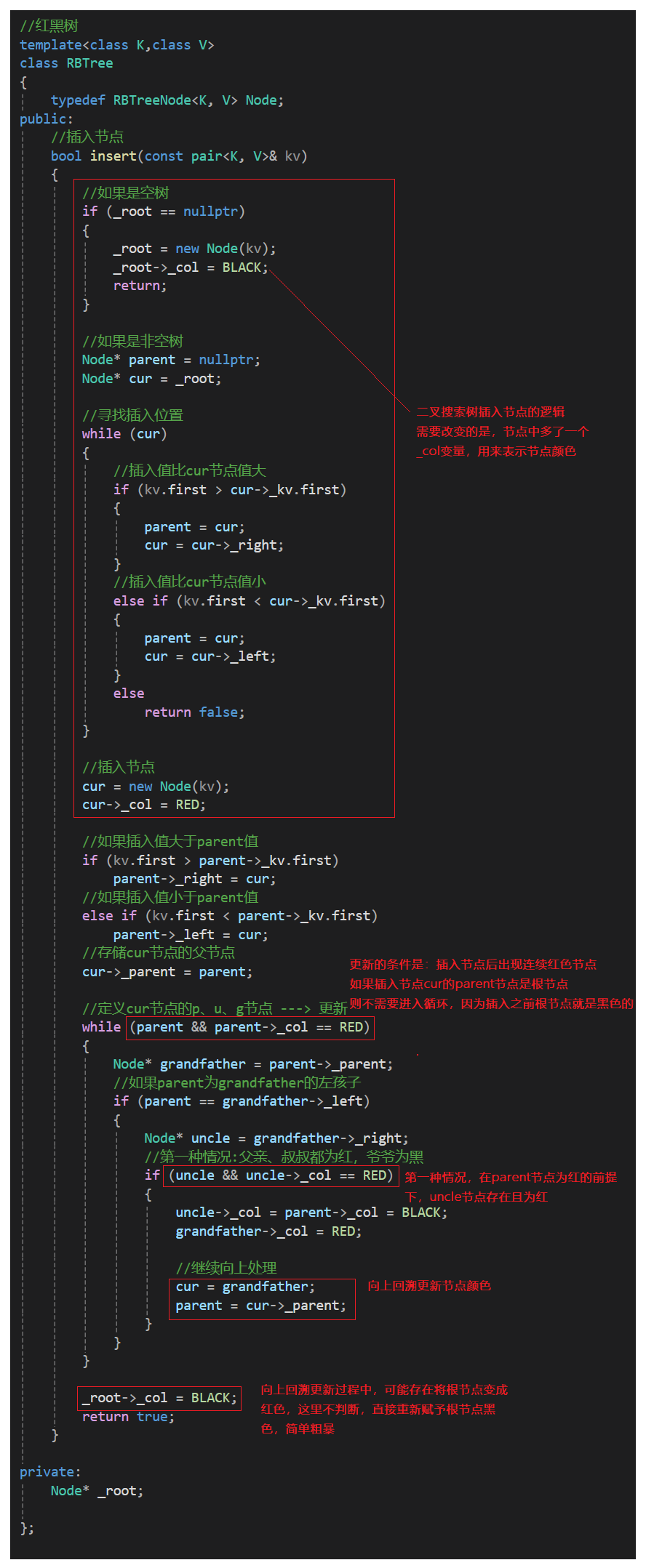
• 1. 紅黑樹插入一個值按照二叉搜索樹的方式插入，插入后只需要觀察是否滿足紅黑樹的4條規則
• 2. 如果是空樹插入，那么新插入的節點要給黑色。但如果是非空樹插入，那么新插入的節點則必須是紅色，因為如果是黑色，就破壞了紅黑樹任意路徑黑色節點相同的規則
• 3.非空樹插入紅色節點后，如果它的父節點是黑色的，那么滿足4條規則，插入結束
• 4.如果非空樹插入紅色節點后，其父節點是紅色的，則違反了紅黑樹任意一條路徑中不能出現連續紅色節點的規則，得進一步分析

---

---

2.2.1 第一種情況:插入節點的父節點和其uncle節點都為紅色，且uncle節點存在

---

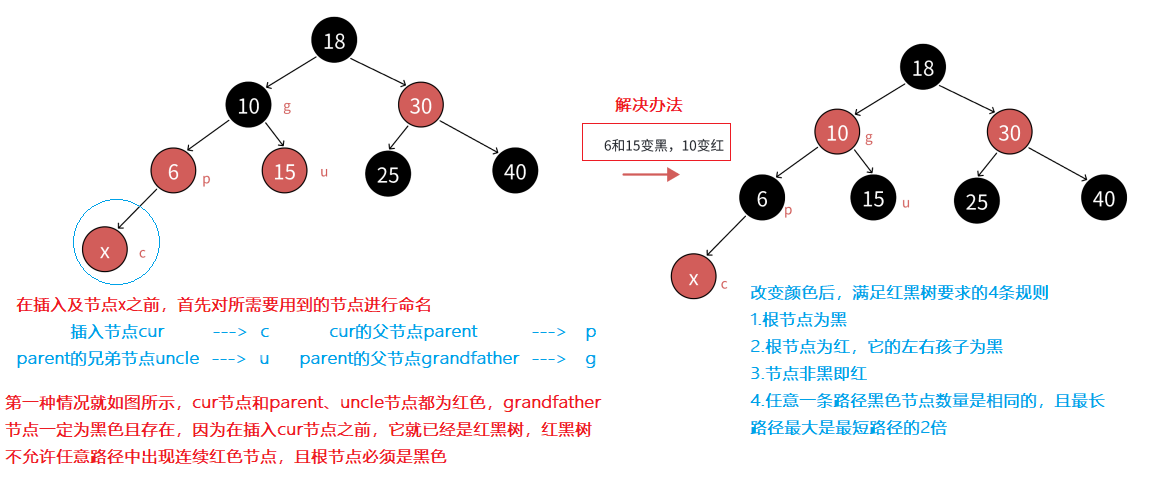
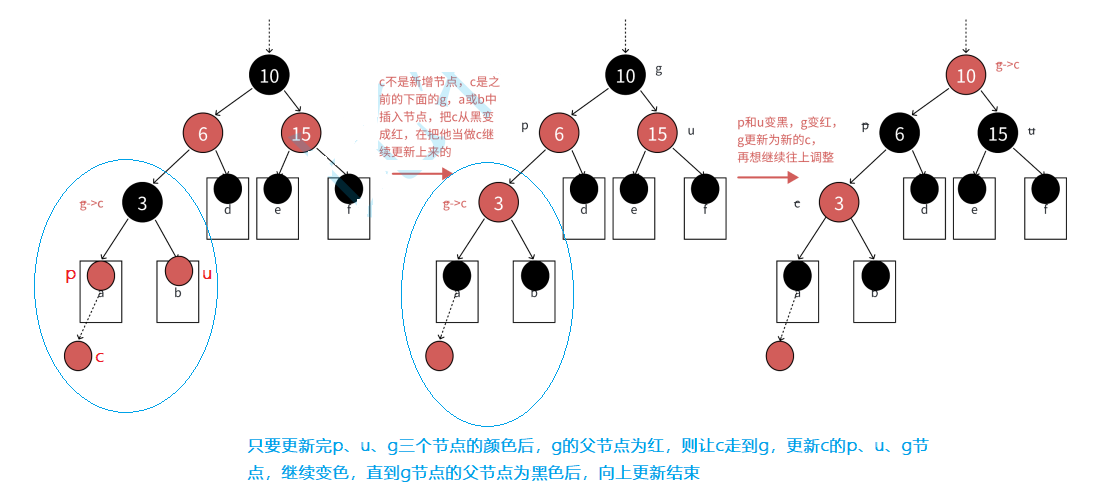
• 注意：上述圖中只是最簡單的一種，無非就是將cur的父節點parent和uncle節點變色(紅→黑)，再將grandfather節點變色(黑→紅)
• 另外cur節點無論插在parent的左邊還是右邊，都滿足上述的變色邏輯
• 當然上圖中這顆樹可能也只是棵子樹，需要繼續向上更新，那什么時候向上更新呢？
• 向上更新的條件: g節點的父節點是紅色時，p、u、g節點變色后需繼續向上更新
• 為什么說g節點的父節點是紅色就得繼續更新呢？因為g節點變完色后是紅色，紅黑樹不允許出現連續的紅色節點

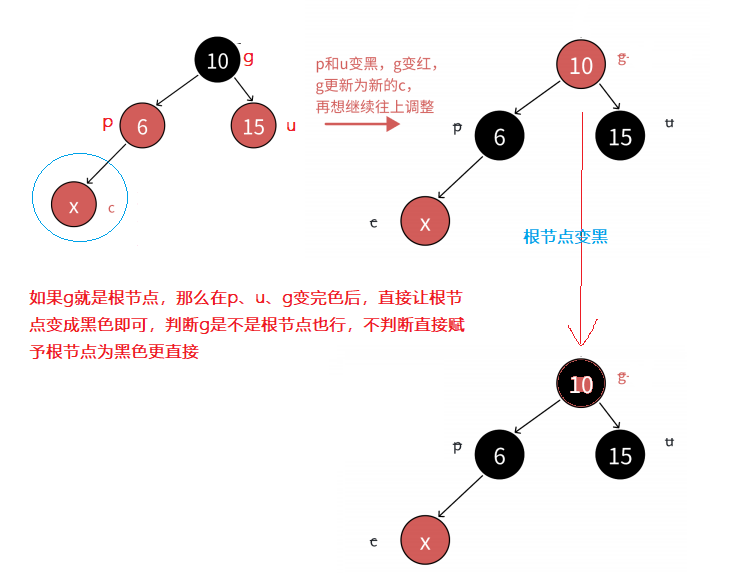
• 向上更新步驟：p、u、g節點變完色后，直接讓cur等于g節點，然后p、u、g節點隨著cur節點更新而更新，直到g節點的父節點為黑，插入結束
• 當然，如果grandfather就是根節點，那么p、u、g節點變完色后，直接讓g節點重新變為黑色，插入結束

---

---

• 代碼實現

---

2.2.2 第2種情況:插入節點cur和其父節點為紅，其uncle節點不存在或者為黑色

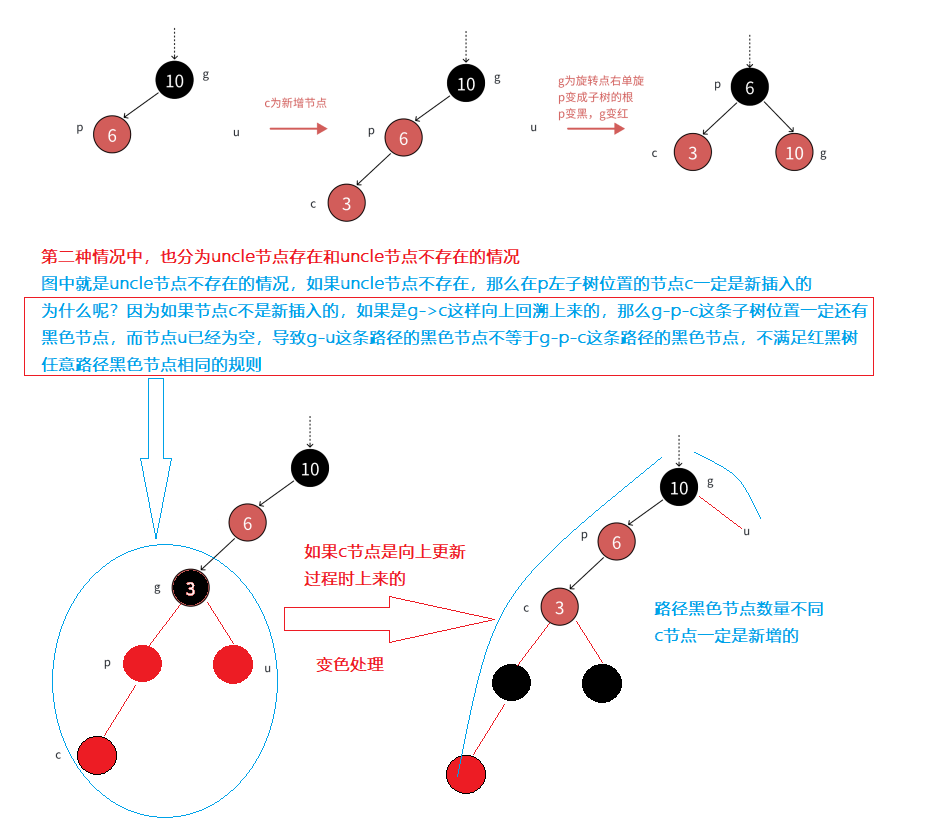
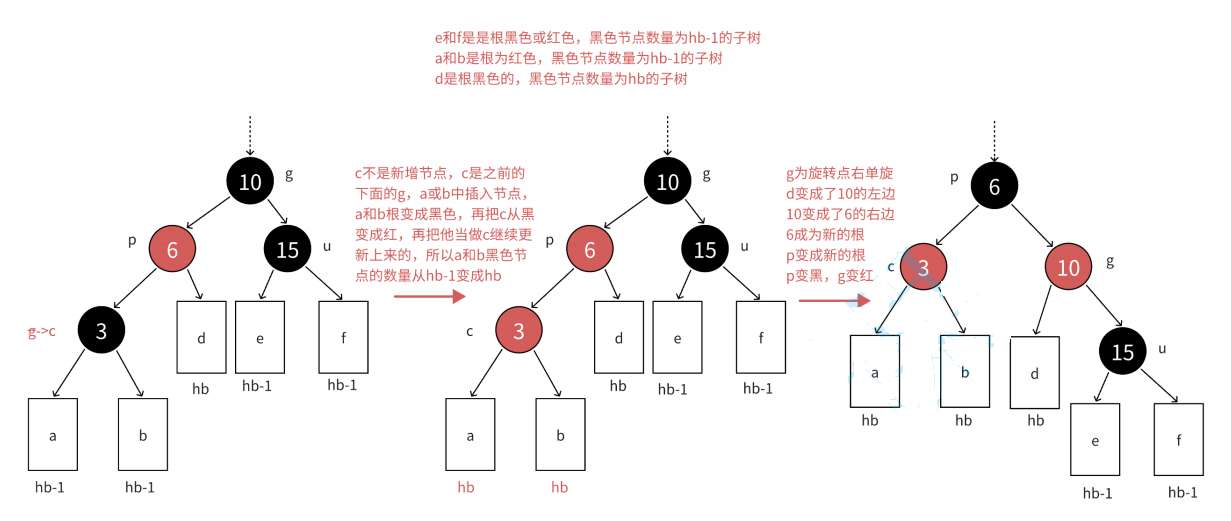
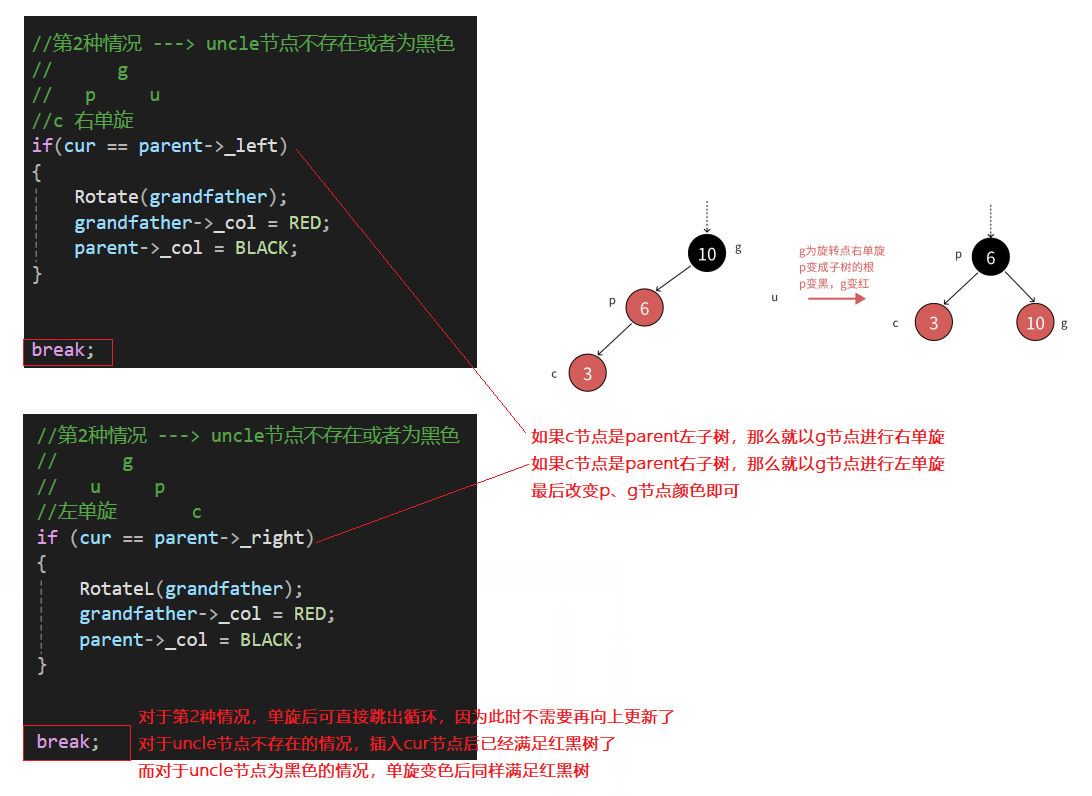
• 這種情況一般是：如果parent是grandfather左子樹節點，cur節點也是p左孩子的情況；或者parent是grandfather右子樹節點，cur節點也是p右孩子的情況
• 因此第2種情況就是：cur節點和parent節點是它們的父節點的左孩子/右孩子方向是保持一致的
• 對于uncle節點不存在的情況，則是直接以節點g為旋轉點進行右單旋，然后分別讓p節點變紅，g節點變黑

---

• 對于uncle節點存在且為黑色的情況，處理情況相同，同樣是以g節點為旋轉點進行右單旋，然后p節點為紅，g節點為黑

---

• 代碼實現

---

2.2.3 第3種情況:uncle節點不存在或者為黑色，且cur節點和parent節點為紅

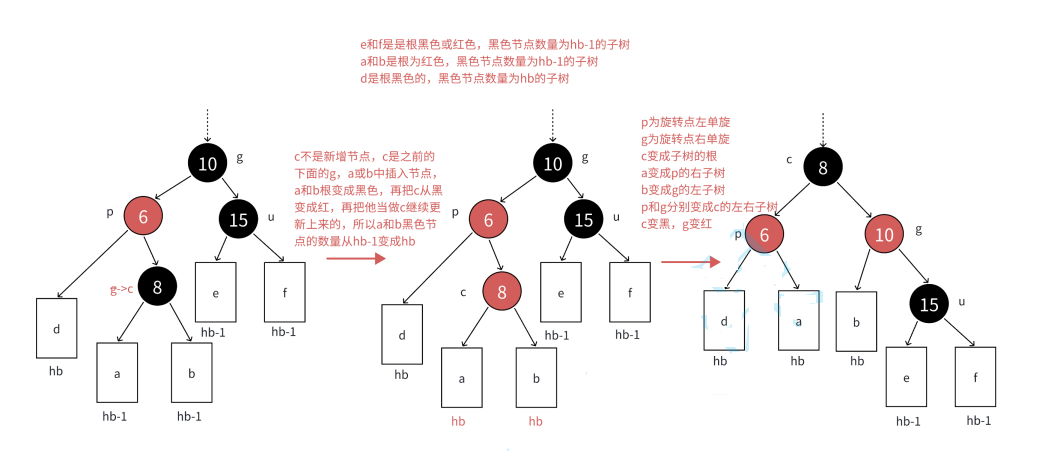
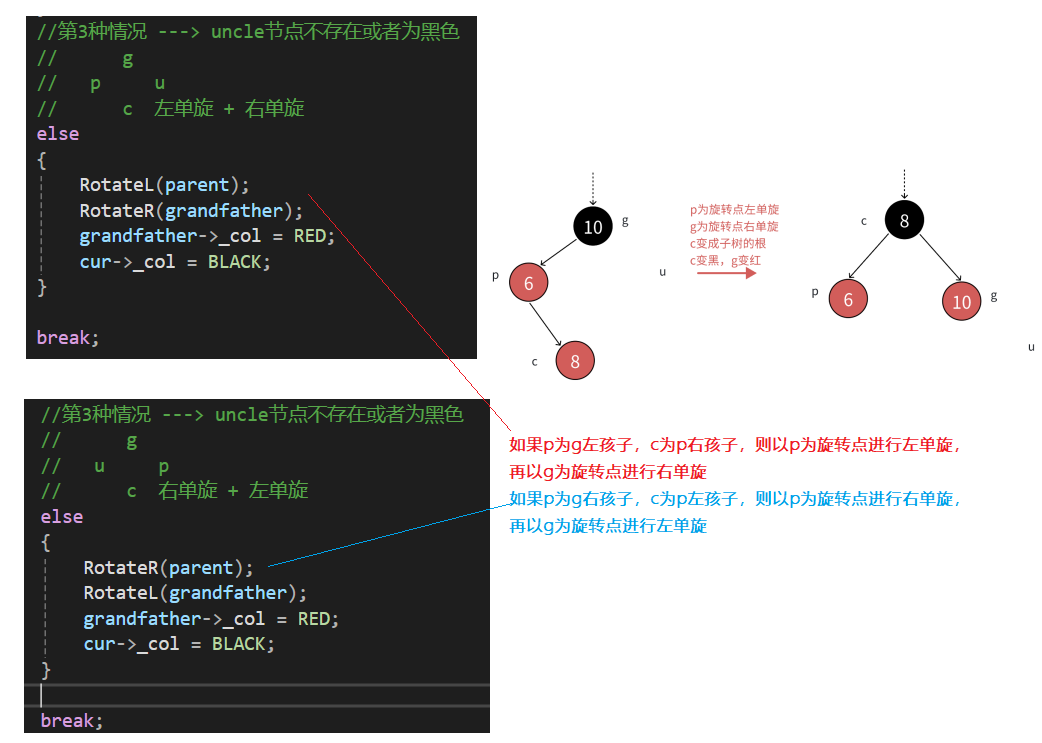
• 這種情況一般是：如果parent是grandfather左子樹節點，cur節點是p右孩子的情況；或者parent是grandfather右子樹節點，cur節點是p左孩子的情況
• 因此第2種情況就是：cur節點和parent節點是它們的父節點的左孩子/右孩子方向不保持一致

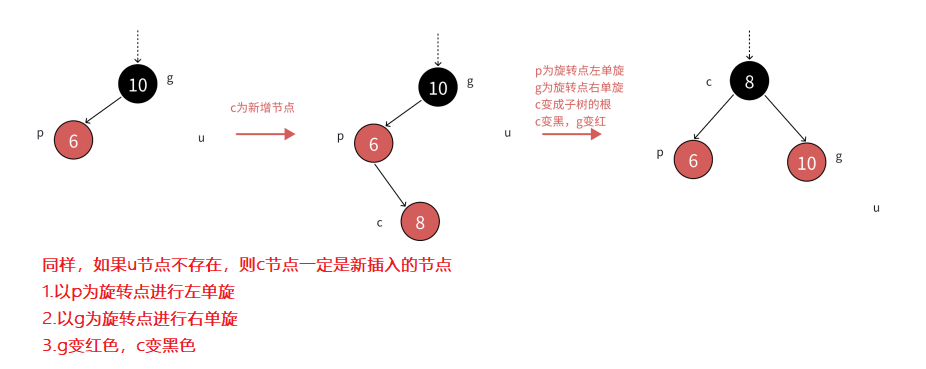
• 第3種情況和第2種情況類似，只是單純一次單旋滿足不了紅黑樹的要求，需要雙旋+變色

---

---

• 同樣和第2種情況類似，情景1：uncle節點不存在

---

• 情景2：uncle節點存在且為黑色

---

• 代碼實現

---

• 當然，對于左右單旋的代碼在上一節AVL樹有詳細講解，這里不過多贅述

2.3 紅黑樹的查找

• 紅黑樹的查找按照二叉搜索樹的方式查找就行，效率O(logN)

//查找
Node* Find(const K& key)
{Node* cur = _root;if (key > cur->_kv.first)cur = cur->_right;else if (key < cur->_kv.first)cur = cur->_left;elsereturn cur;return nullptr;
}

2.4 紅黑樹的驗證

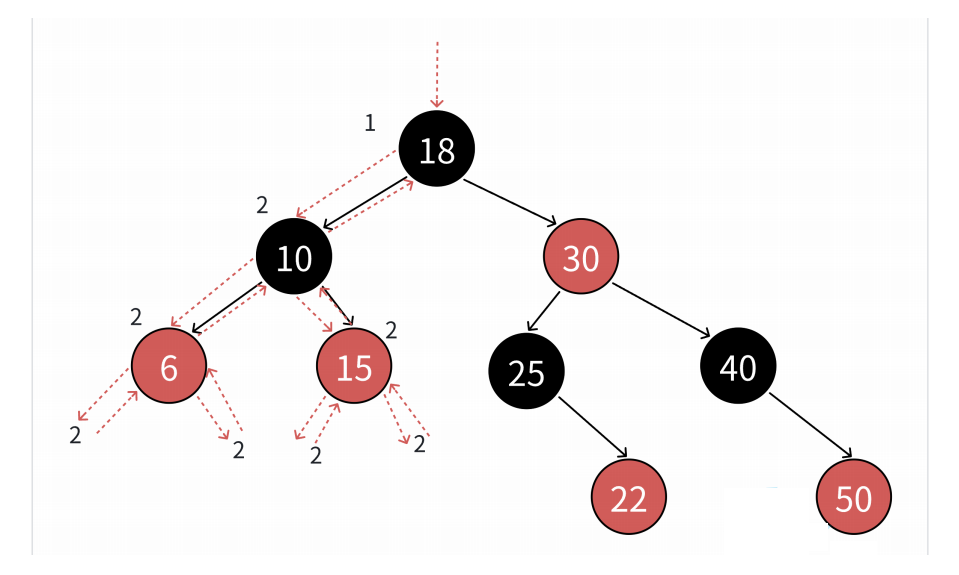
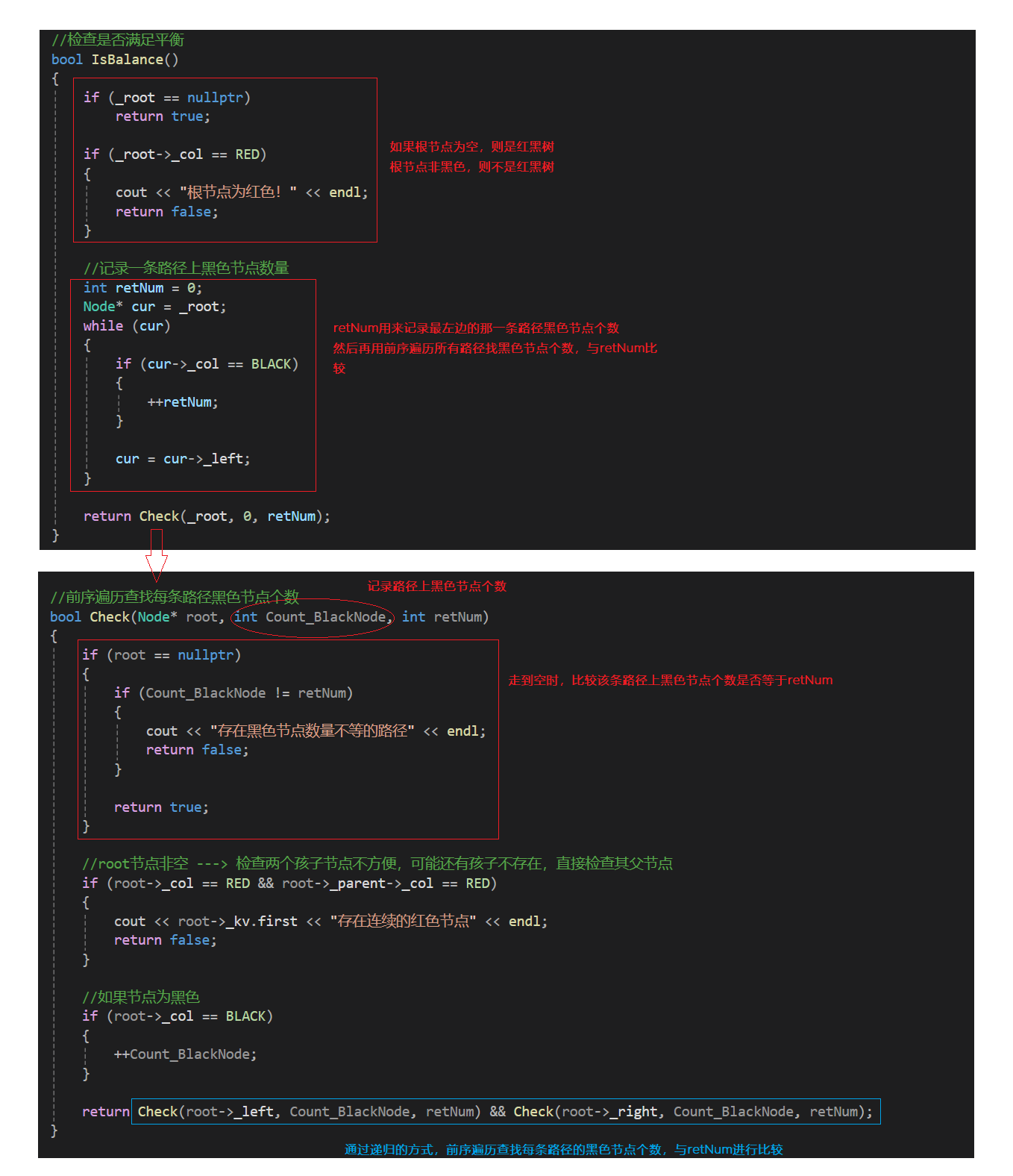
• 這里獲取最長路徑和最短路徑，檢查最長路徑不超過最短路徑的2倍是不可行的，因為就算滿足這個條件，紅黑樹也可能顏色不滿足規則，當前暫時沒出問題，后續繼續插入還是會出問題的。所以我們還是去檢查4點規則，滿足這4點規則，一定能保證最長路徑不超過最短路徑的2倍
• 1. 規則1枚舉顏色類型，天然實現保證了顏色不是黑色就是紅色
• 2. 規則2直接檢查根即可
• 3. 規則3前序遍歷檢查，遇到紅色結點查孩子不太方便，因為孩子有兩個，且不一定存在，反過來檢查父親的顏色就方便多了
• 4. 規則4前序遍歷，遍歷過程中用形參記錄跟到當前結點的blackNum(黑色結點數量)，前序遍歷遇到黑色結點就++blackNum，走到空就計算出了一條路徑的黑色結點數量。再任意一條路徑黑色結點數量作為參考值，依次比較即可

---

• 代碼實現

---

3. 代碼

• RBTree.h代碼

#pragma once
#include <iostream>
using namespace std;//枚舉常量
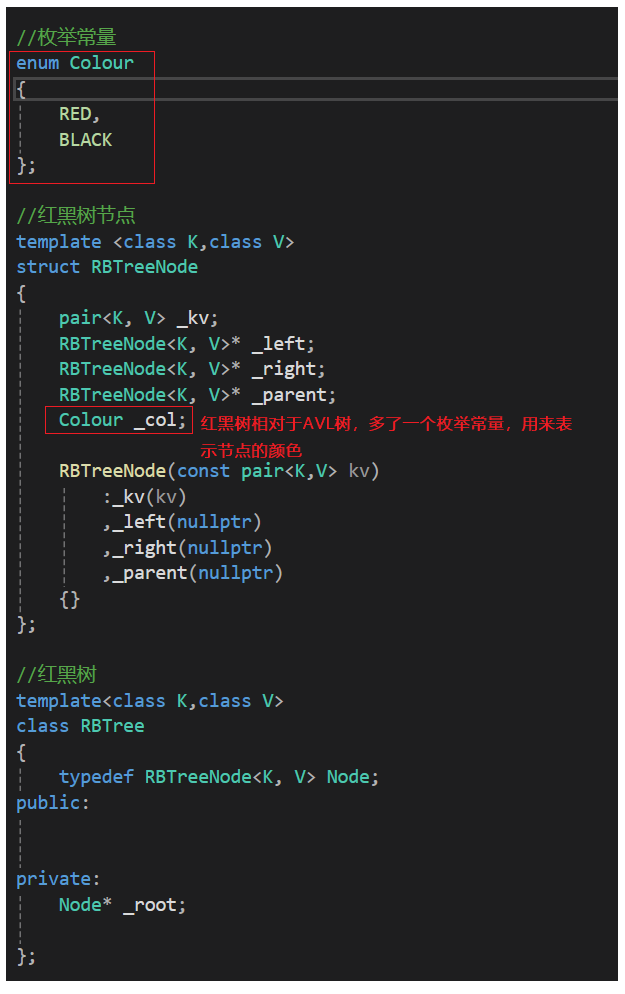
enum Colour
{RED,BLACK
};//紅黑樹節點
template <class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K,V> kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};//紅黑樹
template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://插入節點bool insert(const pair<K, V>& kv){//如果是空樹if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//如果是非空樹 Node* parent = nullptr;Node* cur = _root;//尋找插入位置while (cur){//插入值比cur節點值大if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}//插入值比cur節點值小else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}elsereturn false;}//插入節點cur = new Node(kv);cur->_col = RED;//如果插入值大于parent值if (kv.first > parent->_kv.first)parent->_right = cur;//如果插入值小于parent值else if (kv.first < parent->_kv.first)parent->_left = cur;//存儲cur節點的父節點cur->_parent = parent;//定義cur節點的p、u、g節點 ---> 更新while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//如果parent為grandfather的左孩子if (parent == grandfather->_left){Node* uncle = grandfather->_right;//第一種情況:父親、叔叔都為紅，爺爺為黑if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;}//第2、3種情況else{//第2種情況 ---> uncle節點不存在或者為黑色//      g//   p     u//c 右單旋if(cur == parent->_left){RotateR(grandfather);grandfather->_col = RED;parent->_col = BLACK;}//第3種情況 ---> uncle節點不存在或者為黑色//      g//   p     u//      c  左單旋 + 右單旋else{RotateL(parent);RotateR(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}//如果parent為grandfather的右孩子else{Node* uncle = grandfather->_left;//第一種情況:父親、叔叔都為紅，爺爺為黑if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//繼續向上處理cur = grandfather;parent = cur->_parent;}//第2、3種情況else{//第2種情況 ---> uncle節點不存在或者為黑色//      g//   u     p//左單旋       cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}//第3種情況 ---> uncle節點不存在或者為黑色//      g//   u     p//      c  右單旋 + 左單旋else{RotateR(parent);RotateL(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}}//直接賦予根節點黑色_root->_col = BLACK;return true;}//左單旋void RotateL(Node* parent){//定義兩個節點指針Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;if (subRL)subRL->_parent = parent;Node* parent_Parent = parent->_parent;parent->_parent = subR;//如果parent為根節點if (parent_Parent == nullptr){_root = subR;subR->_parent = nullptr;}//如果parent不是根節點else{//如果旋轉之前parent所在的整個子樹為根節點的左子樹if (parent_Parent->_left == parent)parent_Parent->_left = subR;elseparent_Parent->_right = subR;subR->_parent = parent_Parent;}}//右單旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;if (subLR)subLR->_parent = parent;Node* parent_Parent = parent->_parent;parent->_parent = subL;//如果parent為根節點if (parent == _root){_root = subL;subL->_parent = nullptr;}//如果parent不是根節點else{if (parent_Parent->_left == parent)parent_Parent->_left = subL;elseparent_Parent->_right = subL;subL->_parent = parent_Parent;}}//中序遍歷輸出AVL樹數據void Inorder(){_Inorder(_root);cout << endl;}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << "-" << root->_kv.second << " ";_Inorder(root->_right);}//紅黑樹節點個數size_t Size(){return _Size(_root);}size_t _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}//查找Node* Find(const K& key){Node* cur = _root;while(cur){if (key > cur->_kv.first)cur = cur->_right;else if (key < cur->_kv.first)cur = cur->_left;elsereturn cur;}return nullptr;}//前序遍歷查找每條路徑黑色節點個數bool Check(Node* root, int Count_BlackNode, int retNum){if (root == nullptr){if (Count_BlackNode != retNum){cout << "存在黑色節點數量不等的路徑" << endl;return false;}return true;}//root節點非空 ---> 檢查兩個孩子節點不方便，可能還有孩子不存在，直接檢查其父節點if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在連續的紅色節點" << endl;return false;}//如果節點為黑色if (root->_col == BLACK){++Count_BlackNode;}return Check(root->_left, Count_BlackNode, retNum) && Check(root->_right, Count_BlackNode, retNum);}//檢查是否滿足平衡bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED){cout << "根節點為紅色！" << endl;return false;}//記錄一條路徑上黑色節點數量int retNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++retNum;}cur = cur->_left;}return Check(_root, 0, retNum);}private:Node* _root = nullptr;
};

• 測試代碼test.cpp

#include"RBTree.h"
#include<vector>
//AVL樹的平衡測試
void RBTreetest1()
{RBTree<int, int> rb1;//常規測試//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//for (auto& e : a)//{//	rb1.insert({ e,e });//}//帶有雙旋的測試用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto& e : a){rb1.insert({ e,e });}rb1.Inorder();cout << "Size:" << rb1.Size() << endl;
}void RBTreetest2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(i + rand());}size_t begin2 = clock();RBTree<int, int> t;for (size_t i = 0; i < v.size(); ++i){t.insert(make_pair(v[i], v[i]));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << "Size:" << t.Size() << endl;t.insert({ 20,20 });cout << t.Find(20) << endl;if (t.IsBalance())cout << "該二叉樹是紅黑樹!" << endl;elsecout << "該二叉樹不是紅黑樹!" << endl;}int main()
{//RBTreetest1();RBTreetest2();return 0;
}