leetcode - 雙指針問題

文章目錄

前言

題1 移動零：

思路：

參考代碼：

題2 復寫零：

思考：

參考代碼：

題3 快樂數：

思考：

參考代碼：

題4 盛最多水的容器：

思考：

參考代碼：

題5 有效三角形的個數：

思考：

參考代碼：

題6 查找總價格為目標值的兩個商品：

思考：

參考代碼：

題7 三數之和：

思考：

參考代碼：

題8 四數之和：

總結

前言

路漫漫其修遠兮，吾將上下而求索；

題1 移動零：

283. 移動零 - 力扣（LeetCode）

提取題干意思：

思路：

數組劃分類題型（數組分塊）：給了我們一個數組，并且制定了一個規則，讓我們在這個規則下將該數值劃分為若干個區間

本題：

利用雙指針，指針cur 從左往右遍歷掃描數組，指針dest指向已處理區域非零元素最后一個位置，圖解如下：

相當于指針cur、dest 將數據劃分為了三段：[0,dest] 為非0的數據區域、[dest+1 , cur-1] 為0的數據區域，[cur,n-1] 為待掃描的數據區域（其中n表示數據個數）；

流程：eg. nums = [0,1,0,3,12]

思路總結：

注：雙指針思想是快排中最核心的思想；雖可以解決快排問題，但是當數據量特別大的時候（例如相同的數據很多時），該方法的時間復雜度就接近N^2，因此快排不能解決比較惡心的數據（重復的數據多）；

參考代碼：

    void moveZeroes(vector<int>& nums) {int n = nums.size();int cur = 0, dest = -1;while(cur<n){if(nums[cur]){++dest;swap(nums[dest] , nums[cur]);}cur++;}}

優化 - cur 的遍歷可以使用范圍for，代碼如下：

    void moveZeroes(vector<int>& nums) {int cur = 0;for(auto& e:nums){if(e) {swap(e , nums[cur]);cur++;}}}

題2 復寫零：

??????1089. 復寫零 - 力扣（LeetCode）

提取題干意思：

思考：

我們先思考一下，異地操作（借助于其他空間）如何實現：

需要一個指針cur在舊數組上遍歷，一個指針dest在新數組上遍歷，當cur 遇到了0 就讓dest 寫兩個0，cur 遇到非0，就讓dest 寫這個數據；圖解如下：

Q1：是否可以從左往右直接使用雙指針？

本題不行，因為遇見0要在原數組上寫兩個0，會覆蓋掉后面的數據；但是如果是刪除值為val 的題，就可以這么做；

Q2：既然從左往右不可行，那么從右往左是否可行呢？

從右往左的話，就需要找到cur 最后一個所要“復寫”的位置，如何找？

這與整個數組中0的個數有關系，可以先利用雙指針（cur,dest）從左往右遍歷（cur遇到0,dest走兩步，非0dest走一步;當cur 走到最后一個數據或者dest 走到最后一個的時候，cur 指向的位置就是最后一個所要“復寫”的位置），找到最后一個所要復寫的位置，然后此時cur 、dest 的位置就是從右往左復寫數據時的位置，思路圖如下：

注：dest 指向有效數據的結尾，初始化為-1；cur 初始化為0；

但是，如果當cur 指向0，而dest 往后走兩步可能就會越界，如果dest 越界了；而此時cur 、dest 的位置會作為從右往左復寫數據時的位置，但是dest 已經越界了，故而這是有問題的；

解決方法：在找位置結束后判斷dest 是否合法（dest小于等于n-1就是合法的范圍?，但是dest 如果越界是一定等于n）;如果合法什么都不做，如果不合法，dest = n-1 ，cur--;arr[n-1] = 0，如下圖：

即，在找最后一個所要復寫的位置的時候，有三種情況回導致循環結束：

參考代碼：

    void duplicateZeros(vector<int>& arr){int n = arr.size();int cur = 0, dest = -1;//先從左往右遍歷，找到cur 指向的最后一個數據while(cur<n){if(arr[cur]==0) dest+=2;else ++dest;//在此過程中dest 可能會越界//在cur 自增前判斷dest 是否越界if(dest >= n-1) break;//因為n-1 是最后一個有效位置 cur++;}//邊界情況處理，dest 越界了一定是為nif(dest==n){arr[n-1] = 0;dest-=2;--cur;}//從先有的cur dest 的位置進行復寫操作while(cur>=0){if(arr[cur]==0){arr[dest--] = 0;arr[dest--] = 0;}else{arr[dest--] = arr[cur];}cur--;}}

題3 快樂數：

202. 快樂數 - 力扣（LeetCode）

提取題干意思：

思考：

根據例子，畫圖思考：eg. 19 、2

對于19，最后得到是1在循環，故而返回的是true;對于2，最后得到的不是1的循環，所以返回false;

要么最后是1，陷入1的循環；要么不是1但是最后陷入一個循環之中

圖解是否感覺有點熟悉？是不是有一點像鏈表，如果轉換成鏈表，就是判斷這鏈表環中的值即可（因為一旦有1，就一定是1為一個單獨的循環);而在鏈表 - 判斷鏈表是否有環，是用快慢雙指針來解決；

可以將本題抽象成鏈表，一個數變化成一個數可以抽象成這些數串聯了起來；并且在本題中不用判斷是否有環，只需要判斷環中的值便可；

需要注意的是，slow 初始化為第一個數據的位置，fast 初始化為slow 的下一個位置；

只需要判斷這兩個值相遇的值是不是1即可，是1就返回true ,不是1則返回false;

在這個過程中是一定成環的；

注：

1、在帶環的鏈表中，快慢雙指針一定會相遇，并且一定會在環中相遇；

2、本題中雖然不像鏈表中是一個一個結點，只是一個一個的數，我們也可以讓數來充當“指針”；不要被指針這個詞限制了思維，此處所講的指針并不是真正的指針，而是在數組中使用雙指針的時候可以用數組下標來充當指針，因此“雙指針”只是一種思想；

本題題干中：，所以就一定回成環，但是如果題干如果沒有給這個提示呢？

那么分析地時候，就會分析出第三種情況：變下去不會成環；存在不成環的情況嗎？如果題干沒有這個提示，我們又該如何解決？

證明：為什么在變化的過程中一定會有環？

我們先來了解一個原理：鴿巢原理（抽屜原理）

注：我們的證明會用到鴿巢原理

取?9999999999 是因為它是 2.1*10^9 同樣位數中的最大的數，可以靠它看一下范圍；

對于 9999999999 來說，經過“操作”它每一位的和為 9^2*10 = 810，也就是9999999999經過“操作”之后所能變成的最大的數，即對于 9999999999 來說有810 個巢，而 2.1*10^9 小于9999999999，那么? 2.1*10^9 經過操作之后的結果一定小于等于9999999999 經過“操作”之后的結果810，即2.1*10^9 的巢得個數一定小于等于810并且大于等于1；

2.1*10^9 的巢得個數：[1，810]

那么一個數如果進行了“操作”大于810 次（操作次數是無限的），必定就會循環，即該數一定成環；（即將大于810 的鴿子放到810 個巢里面，必定有一個巢中的鴿子數量大于1）就可以證明沒有第三種情況：變下去不會成環；

經過上述證明，數據在變化的過程中一定會成環；

參考代碼：

    //獲取一個數的每一個位置上的平方和int getbit(int n){int tmp = n, sum  = 0;while(tmp){int t  = tmp%10;//每一位sum += t*t;//平方和tmp/=10;//迭代}return sum;}bool isHappy(int n) {//通過鴿巢原理可以證明一定成環，所以可以利用快慢雙指針來解決這個問題//注意slow 與 fast 的初始化！int slow = n , fast = getbit(n);//當slow 與 fast 相遇的時候，一定在環中相遇，此時只需要判斷相遇的值便可while(slow!=fast){//slow 一次走一步//fast 一次走兩部slow = getbit(slow);fast = getbit(fast);fast = getbit(fast);}if(slow == 1) return true;else return false;}

可以優化一下上面的參考代碼，優化代碼如下：

    //獲取一個數的每一個位置上的平方和int getbit(int n){int tmp = n, sum  = 0;while(tmp){int t  = tmp%10;//每一位sum += t*t;//平方和tmp/=10;//迭代}return sum;}bool isHappy(int n) {//通過鴿巢原理可以證明一定成環，所以可以利用快慢雙指針來解決這個問題//注意slow 與 fast 的初始化！int slow = n , fast = getbit(n);//當slow 與 fast 相遇的時候，一定在環中相遇，此時只需要判斷相遇的值便可while(slow!=fast){//slow 一次走一步//fast 一次走兩部slow = getbit(slow);fast = getbit(getbit(fast));}return slow==1;}

題4 盛最多水的容器：

11. 盛最多水的容器 - 力扣（LeetCode）

數據范圍：

例子：

思考：

解法一：暴力解法

將所有兩兩組合的情況均列舉出來，找到其中的最大值即可；此處的數據量約有 10萬，使用暴力解法的時間復雜度為 O(N^2) ,一定會超時的，不過此處我們還是嘗試一下用暴力解法是否能過：

測試用例能通過，但是提交之后：

解法二：利用單調性使用雙指針

為什么會想到用單調性？

如果想要找到兩數相乘再乘以其底面積的最大值，一定是從左邊區域中找一個最大的乘以右邊區域中最大的數；使用雙指針一個從左邊開始，一個從右邊開始，誰小誰就往自己所在的方向移動；而如果有一個木桶，它的板高度不一樣，它所能所能存多少水是由最短的板決定的，所以我們該用短板才會有效果，而桶底也是變化的，所以還需要一個變量來記錄體積；

例子：

思路總結：定義兩個指針left right ,根據這兩個指針指向的數據，記錄計算出來的體積，誰小誰移動，循環下去更新得到的最大值；循環條件：left<right;

參考代碼：
?

    int maxArea(vector<int>& height) {//體積由短板決定int left = 0 , right = height.size()-1 ,ret = INT_MIN;while(left<right){//體積 = 短板長度*底面積int v = (height[left]<height[right]?height[left] : height[right]) * (right-left);ret = max(ret , v);//誰小誰移動if(height[left]>height[right]) right--;else left++;}return ret;}

題5 有效三角形的個數：

611. 有效三角形的個數 - 力扣（LeetCode）

題干：

數據范圍：

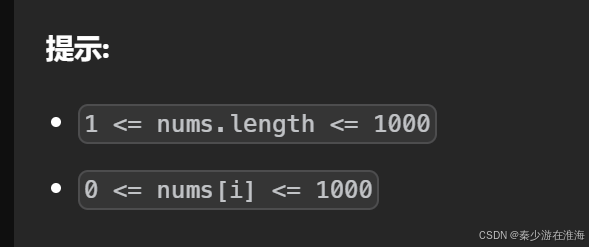
例子：

思考：

本題無非就是枚舉出所有的三個數，然后判斷這三個數能否組成三角形；

Q：如何判斷三個數能否構成三角形？

首先會想到的是“兩邊之和大于第三邊”，讓三個數兩兩組合然后與第三個數比較，看是否符合就行，但是這種判斷方式需要判斷三次，效率上有點低，有沒有高效點的判斷方法？

第二種判斷方法：讓較小兩邊相加與最長邊比較，如果是大于則就可以構成三角形；

因為最長邊一定是大于較小邊的（另外兩個情況），所以只要保證讓較小兩邊相加大于最長邊便可，圖解如下：

而對于枚舉，首先我們一定會想到的是暴力解法，利用循環枚舉出所有的情況，然后判斷，這種方法的時間復雜度為O(N^3)，先試一下暴力解法能否通過：

使用暴力解法，測試用例可以通過，但是提交：

不能使用暴力解法解決，還能怎么做？

我們前面曾說，判斷兩個數能夠構成三角形，如果得到了這三個數的大小關系，可以拿較小的兩個數與最大的那一個數進行比較，不可能每次拿到三個數就先比較大小吧？暴力枚舉依然是個痛處，既然在比較的時候就要知道數據的大小關系，那么我們可以先對數據進行排序，利用數據的單調性以及三指針；

當 b + c > a 時（即 b 和 c 指向的數據之和大于 a 指向的數據），這三個數必定可以構成三角形。此時，區間 [b+1, c-1] 內的數據均大于 b，且與 c 相加后仍滿足大于 a 的條件，那么就有（c-1-b+1）個數符合要求，利用變量記錄；然后?c 減 1，繼續在下一個區間進行判斷
當 b + c < a 時（即 b 和 c 指向的數據之和小于 a 指向的數據），這三個數無法構成三角形。此時，區間 [b+1, c-1] 內的數據均小于 c 指向的數據，不符合要求，無需記錄，直接讓?b 加 1，繼續在下一個區間中尋找符合條件的組合。

最大的數a?從右往左遍歷，b初始化為0，c初始化為a-1;

這就是解法二：利用單調性，使用雙指針方法來解決問題，稍微總結一下：

1、先固定最大的數
2、在最大的數的左區間中，使用雙指針算法，快速統計出符合要求的三元組的個數；

舉個例子：

參考代碼：

    int triangleNumber(vector<int>& nums) {//先對數據進行排序處理sort(nums.begin() , nums.end());int n = nums.size();int a = n-1 , ret = 0;//指向最大的指針for( ; a>=2;a--){int b = 0, c = a-1;//讓較小的兩個while(b<c){if(nums[b]+nums[c]>nums[a]) //b->[b,c-1] 區間中的數據均合理 {ret+=(c-1-b+1);c--;//去下一個區間}else //不符合要求，那么c->[b+1,c] 中的均不符合{b++;}}}return ret;}

題6 查找總價格為目標值的兩個商品：

LCR 179. 查找總價格為目標值的兩個商品 - 力扣（LeetCode）

題目：

數據范圍：

例子：

思考：

方法一：暴力解法

將所有的兩個數的組合列舉出來然后進行比較

偽代碼：

可以試一下用暴力解法能否通過算法：

提交：

暴力解法不行；

方法二：題干中說過price 數組中的數據為升序，我們可以利用好單調性；最先想到的可能是二分算法，但是此處不推薦使用二分，我們可以利用單調性+雙指針來解決；

設置兩個指針：left 與right , 讓left 指向最左的數據，讓right 指向最大的數據，如果left + right 的結果大于 target ，那么right--;如果left + right 的結果小于target 那么left++;圖解如下：

總結算法邏輯：

參考代碼：

    vector<int> twoSum(vector<int>& price, int target){//利用數據的單調性+雙指針int n = price.size();int left = 0, right = n-1;while(left < right){if(price[left]+price[right] > target) right--;else if(price[left]+price[right] < target) left++;else return {price[left] , price[right]};}//沒有找到，返回空return{};}

題7 三數之和：

15. 三數之和 - 力扣（LeetCode）

題干如下：

數據范圍：

例子：

思考：

即在數組中找到三個不重復的數據讓其相加為0；

根據前面做過的題的經驗，我們可以先將數據進行排序處理；

Q：如何讓找到的三個數據不重復呢？

可以首先將nums 中的數據進行去重處理，利用set就可以了;

解法一：暴力解法：排序 + 暴力枚舉 + 利用set 進行去重

此處就不驗證暴力解法是否能通過了，數據量有10萬，時間復雜度為O(N^3) 的算法一定會超時；

解法二：排序 +? 固定一個數a ，利用雙指針找到何為-a 的兩個值

這樣的話，”利用雙指針找到何為-a 的兩個值“ 的思路就與題6中的思路非常像；

Q：那么去重呢？

筆試中可以利用容器set進行去重，但是在面試中不推薦這么做；本題，我們開始就對數據進行了排序處理，那么相同的數據就已經放在了一起；當我們找到了一個結果的時候left 和 right 該如何移動？left 和 right 要跳過與當前所指數相同的重復的數據，繼續縮小空間繼續查找，同樣的，我們固定的數a 也需要進行去重處理，當使用完一輪雙指針算法之后，a 也需要跳過重復的數據；

要做到不重不漏；

參考代碼：

    vector<vector<int>> threeSum(vector<int>& nums) {//首先先對數組進行排序sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> ret;for(int i = 0 ;i< n; ){int left = i+1, right = n-1;while(left < right){int target = -nums[i];int sum = nums[left] + nums[right];if(sum > target) right--;else if(sum < target) left++;else{ret.push_back({nums[i], nums[left] , nums[right]});left ++ ,right--;//去重while( left < right && nums[left] == nums[left-1]) left++;while( left < right && nums[right] == nums[right+1]) right--;}}//一輪雙指針結束之后，還要對固定的數進行去重處理++i;while(i<n && nums[i] == nums[i-1]) ++i;}return ret;}

題8 四數之和：

18. 四數之和 - 力扣（LeetCode）

題干：

數據范圍：

例子：

思考：

本題的解題思路非常淺顯：找到4個數 + 判斷是否相加為target

找數就有講究了，要么暴力枚舉，要么使用比較巧妙的方法，同樣的，本題要求不包含重復的數據，我們可以考慮使用set 去重；

通過數據范圍就知道，我們要使用long long ；

解法一：排序 + 暴力解法 + 利用set去重

本題的數據量很大，并且要暴力枚舉出4個數，實踐復雜度非常高，一定會超時，此處就不演示了；

解法二：排序 + 雙指針

可以參考上題三數之和的思路；

首先是將數據進行排序，利用數據有序的特點可以提高效率；然后是固定一個數，再固定一個數，剩下兩個數利用雙指針；可以理解為，我們先固定一個數a，那么題目就變成在除了固定的的這個數中找和為（target-a）的三個數：

最后需要做到“不重不漏”，本題會設置三個循環，兩個循環用來固定兩個數，一個循環適用于雙指針，這三個循環都需要關注去重處理（如果不用set 去重的話）；而關于不漏，在雙指針查找的過程中，我們要在left 和 right 中找到和為目標值時，不能直接結束當前的雙指針查找循環，而是要left++,right-- 且left<right ，繼續查找下去；

初次嘗試：；

計算目標值的時候，記得用long long!

參考代碼：

    vector<vector<int>> fourSum(vector<int>& nums, int target) {//首先對數據進行排序sort(nums.begin() , nums.end());int n = nums.size();vector<vector<int>> ret;//固定數afor(int i = 0; i<n; ){//固定數bfor(int j = i+1;j<n; ){long long t = ( long long)target - nums[i] -nums[j];//雙指針查找int left = j+1,right = n-1;while(left < right){int sum = nums[left] + nums[right];if(sum > t) right--;else if(sum < t) left++;else{//將數據放入數組中ret.push_back({nums[i] , nums[j] , nums[left] , nums[right]});//去重left++,right--;while(left < right && nums[left] == nums[left-1]) left++;while(left < right && nums[right] == nums[right+1]) right--;}}//固定的第二個數的去重++j;while(j<n && nums[j] == nums[j-1])j++;}//固定的第一個數的去重++i;while(i<n && nums[i] == nums[i-1])i++;}return ret;}