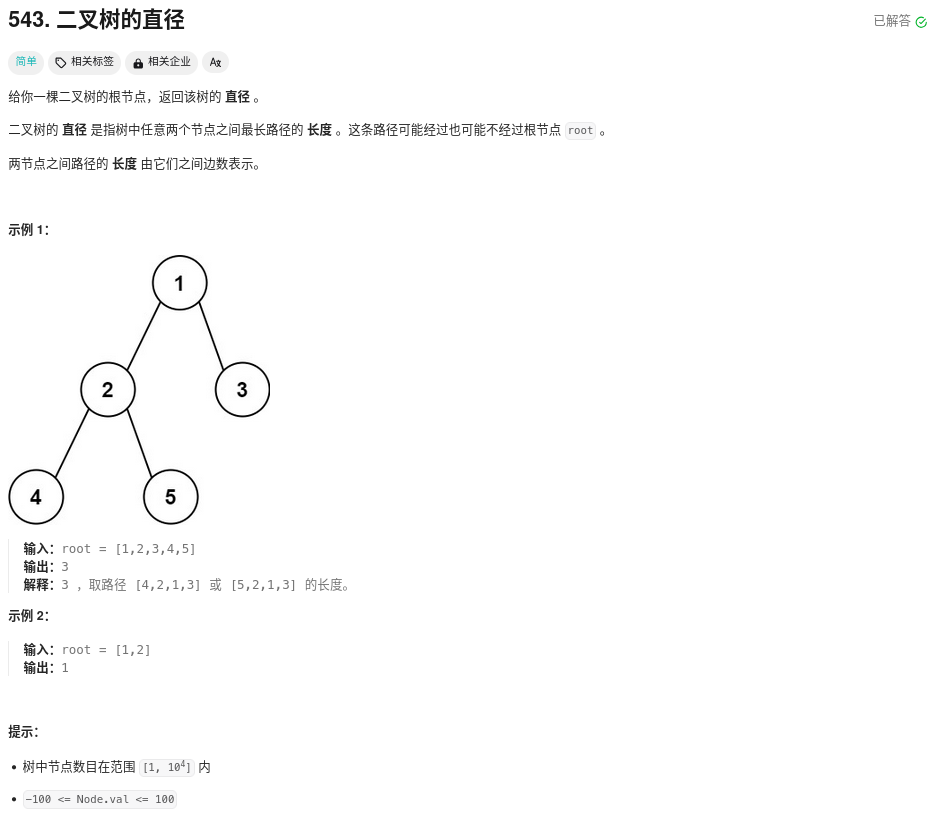
這道題本來想到可以用遞歸做，但是還是沒想明白，最后還是去看靈神題解了，感覺這道題最大的收獲就是鞏固了我對lambda表達式的掌握。
按照靈神的思路，直徑可以理解為從一個葉子出發向上，在某個節點處拐彎，然后向下到達另一個葉子，從而我們可以得到由兩條鏈拼接起來的直徑（也可能只有一條鏈）。既然直徑一定會在某個節點拐彎，那我們可以枚舉每個點，假設在這個節點拐彎，然后分別計算該節點的左右子樹最長鏈（最大深度）然后+2，就得到了以當前節點為根節點的直徑，我們使用一個全局變量來維護二叉樹的最大直徑，每當計算一個節點為根節點的最大直徑時，就進行比較和更新。這里我們遞歸的作用并不是計算每個節點的直徑，而是計算每個節點的左右子樹中的最大鏈長，計算完之后二者相加，再順帶計算出當前節點的直徑。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int diameterOfBinaryTree(TreeNode* root) {int result = 0;//定義一個可以遞歸調用的lambda表達式//[可以訪問的外部變量] (參數列表) -> 函數返回值類型 {函數體}auto dfs = [&] (this auto&& dfs, TreeNode* root) -> int {if(!root) return -1;   //遇到空節點則返回-1//注意，這里的鏈長不是直徑，鏈長是不會拐彎的int left_len = dfs(root -> left) + 1;  //左子樹最大鏈長 + 1int right_len = dfs(root -> right) + 1;   //右子樹最大鏈長 + 1result = max(result, left_len + right_len);   //在當前節點處拐彎能否取得更大值return max(left_len, right_len);};//這里不要用result接收，因為dfs不是用來計算二叉樹直徑的//而是用來計算左右子樹中的最大鏈長的dfs(root);  return result;}
};