目錄

題目描述

解法1：動態規劃

代碼實現

---

題目鏈接

題目描述

給定兩個字符串 text1 和 text2，返回這兩個字符串的最長公共子序列的長度。

一個字符串的 子序列 是指這樣一個新的字符串：它是由原字符串在不改變字符的相對順序的情況下刪除某些字符（也可以不刪除任何字符）后組成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。兩個字符串的「公共子序列」是這兩個字符串所共同擁有的子序列。

若這兩個字符串沒有公共子序列，則返回 0。

示例 1:

• 輸入：text1 = "abcde", text2 = "ace"

• 輸出：3

• 解釋：最長公共子序列是 "ace"，它的長度為 3。

示例 2:

• 輸入：text1 = "abc", text2 = "abc"

• 輸出：3

• 解釋：最長公共子序列是 "abc"，它的長度為 3。

示例 3:

• 輸入：text1 = "abc", text2 = "def"

• 輸出：0

• 解釋：兩個字符串沒有公共子序列，返回 0。

提示:

• 1 <= text1.length <= 1000

• 1 <= text2.length <= 1000 輸入的字符串只含有小寫英文字符。

解法1：動態規劃

本題和動態規劃：718. 最長重復子數組區別在于這里不要求是連續的了，但要有相對順序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

繼續動規分析如下：

1. 確定dp數組（dp table）以及下標的含義

dpi：長度為[0, i - 1]的字符串text1與長度為[0, j - 1]的字符串text2的最長公共子序列為dpi

1. 確定遞推公式

主要就是兩大情況： text1[i - 1] 與 text2[j - 1]相同，text1[i - 1] 與 text2[j - 1]不相同如果text1[i - 1] 與 text2[j - 1]相同，那么找到了一個公共元素，所以dpi = dpi - 1 + 1;如果text1[i - 1] 與 text2[j - 1]不相同，那就看看text1[0, i - 2]與text2[0, j - 1]的最長公共子序列 和 text1[0, i - 1]與text2[0, j - 2]的最長公共子序列，取最大的。即：dpi = max(dpi - 1, dpi);

代碼如下：

if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

1. dp數組如何初始化

先看看dpi應該是多少呢？test1[0, i-1]和空串的最長公共子序列自然是0，所以dpi = 0;

同理dp0也是0。其他下標都是隨著遞推公式逐步覆蓋，初始為多少都可以，那么就統一初始為0。

代碼：

vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

1. 確定遍歷順序

從遞推公式，可以看出，有三個方向可以推出dpi，如圖：

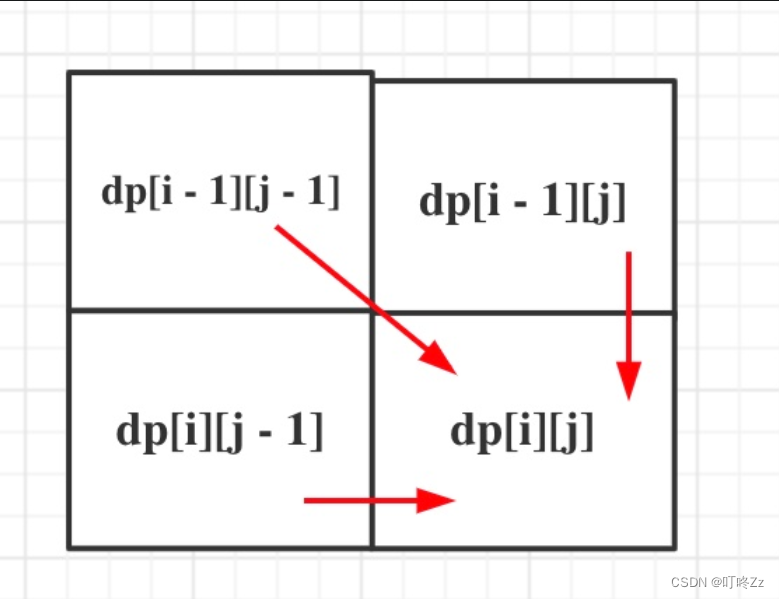
那么為了在遞推的過程中，這三個方向都是經過計算的數值，所以要從前向后，從上到下來遍歷這個矩陣。

代碼實現

class Solution {public int longestCommonSubsequence(String text1, String text2) {int len1 = text1.length();int len2 = text2.length();
?int[] dp = new int[len2+1];
?for (int i = 0; i < len1; i++) {int pre = dp[0];for (int j = 1; j <= len2; j++) {int cur = dp[j];if (text1.charAt(i) == text2.charAt(j-1)) {dp[j] = pre + 1;} else {dp[j] = Math.max(dp[j-1], dp[j]);}pre = cur;}}
?return dp[len2];
?}
}