題解一：

? ? ? ? 按列求：分別考慮每一列的雨水高度，某列的雨水高度只與其左側最高墻和右側最高墻有關，一種情況是該列比左右側的墻都低，則根據木桶效應該列雨水高度為min(左側墻高，右側墻高)-列高，而其余情況該列均無法接住雨水。找左右側最高墻時可以用動態規劃進行優化，對于第n列，左側最高墻為max(第n-1列的左側最高墻，第n-1列高度)，右側最高墻為max(第n+1列的右側最高墻，第n+1列高度)，最后將每列的雨水高度相加即可。

class Solution {public int trap(int[] height) {int len = height.length;int water = 0;int[] left = new int[len];int[] right = new int[len];left[0] = 0;right[len - 1] = 0;for (int i = 1; i < len; i++) {left[i] = Math.max(left[i - 1], height[i - 1]);}for (int i = len - 2; i >= 0; i--) {right[i] = Math.max(right[i + 1], height[i + 1]);}for (int i = 1; i < len - 1; i++) {if (height[i] < left[i] && height[i] < right[i]) water += Math.min(left[i], right[i]) - height[i];}return water;}
}

題解二：

? ? ? ? 單調棧：由于只有凹型結構可以接住雨水，因此我們可以找出高度圖中的所有凹型結構，計算接住雨水的量總和。我們利用單調棧來求解，要滿足凹型結構則需要至少三根柱子，并且高度呈先遞減后遞增的趨勢。遍歷數組依次入棧，如果是遞減結構則繼續入棧，如果出現遞增，則判斷是否滿足凹型結構（棧中至少有兩個元素），如果不滿足則說明只能形成兩根遞增結構的柱子，此時將左柱子出棧，如果滿足則根據水桶效應計算三個柱子能接住的雨水量，并將中部柱子出棧。以下是官方給出的動畫演示（來源. - 力扣（LeetCode））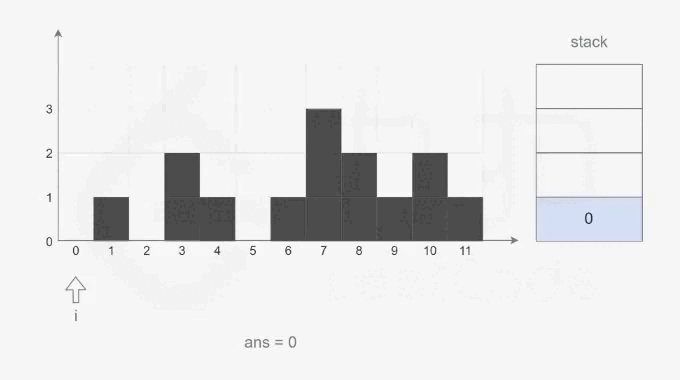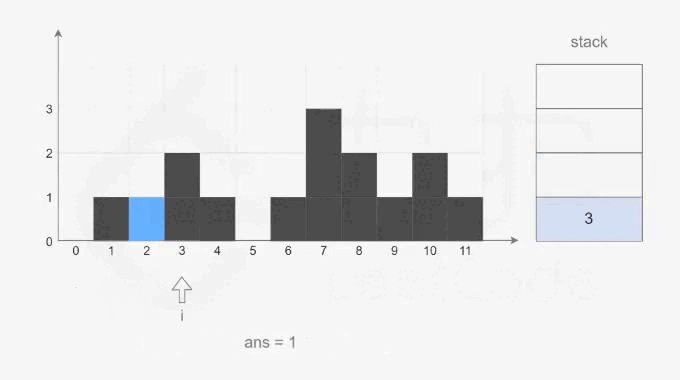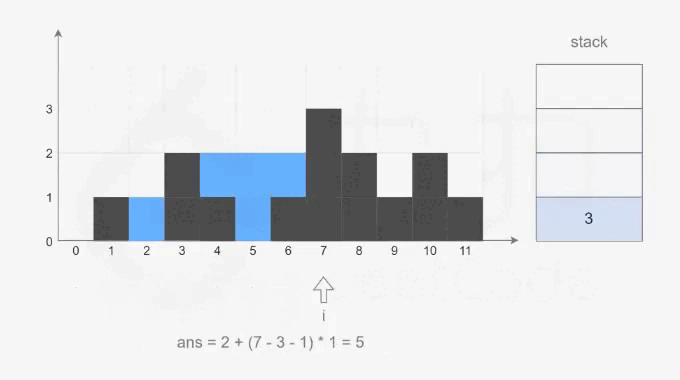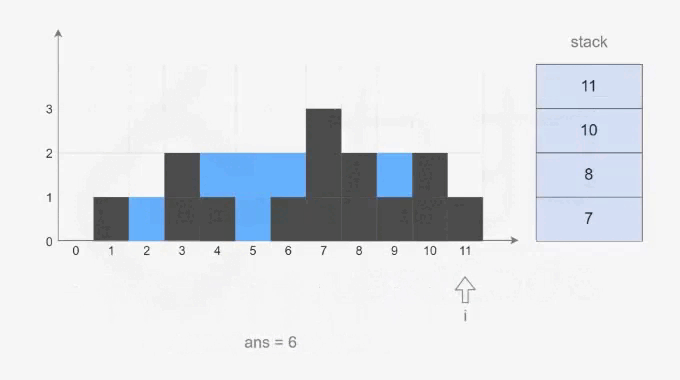

import java.util.Stack;class Solution {public int trap(int[] height) {int len = height.length;Stack<Integer> stack = new Stack<>();int water = 0;for (int i = 0; i < len; i++) {while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int temp = stack.pop();if (stack.isEmpty()) break;else {int left = stack.peek();water += (i - left - 1) * (Math.min(height[i], height[left]) - height[temp]);}}stack.push(i);}return water;}
}