---

一.什么是環形鏈表？

環形鏈表是一種特殊類型的鏈表數據結構，其最后一個節點的"下一個"指針指向鏈表中的某個節點，形成一個閉環。 換句話說，鏈表的最后一個節點連接到了鏈表中的某個中間節點，而不是通常情況下連接到空指針 (null)

二.環形鏈表的例題（力扣）

給你一個鏈表的頭節點?head?，判斷鏈表中是否有環。

如果鏈表中有某個節點，可以通過連續跟蹤?next?指針再次到達，則鏈表中存在環。 為了表示給定鏈表中的環，評測系統內部使用整數?pos?來表示鏈表尾連接到鏈表中的位置（索引從 0 開始）。注意：pos?不作為參數進行傳遞?。僅僅是為了標識鏈表的實際情況。

如果鏈表中存在環?，則返回?true?。 否則，返回?false?。

輸入：head = [3,2,0,-4], pos = 1
輸出：true
解釋：鏈表中有一個環，其尾部連接到第二個節點。

這個題目，我們的做法是快慢指針思想，先設置fast和slow兩個指針指向鏈表的開始，慢的一次走一步，快的一次走兩步，如果不帶環，fast的就為空，如果帶環，fast就會在環里追上slow。我們來畫圖來看他的情況。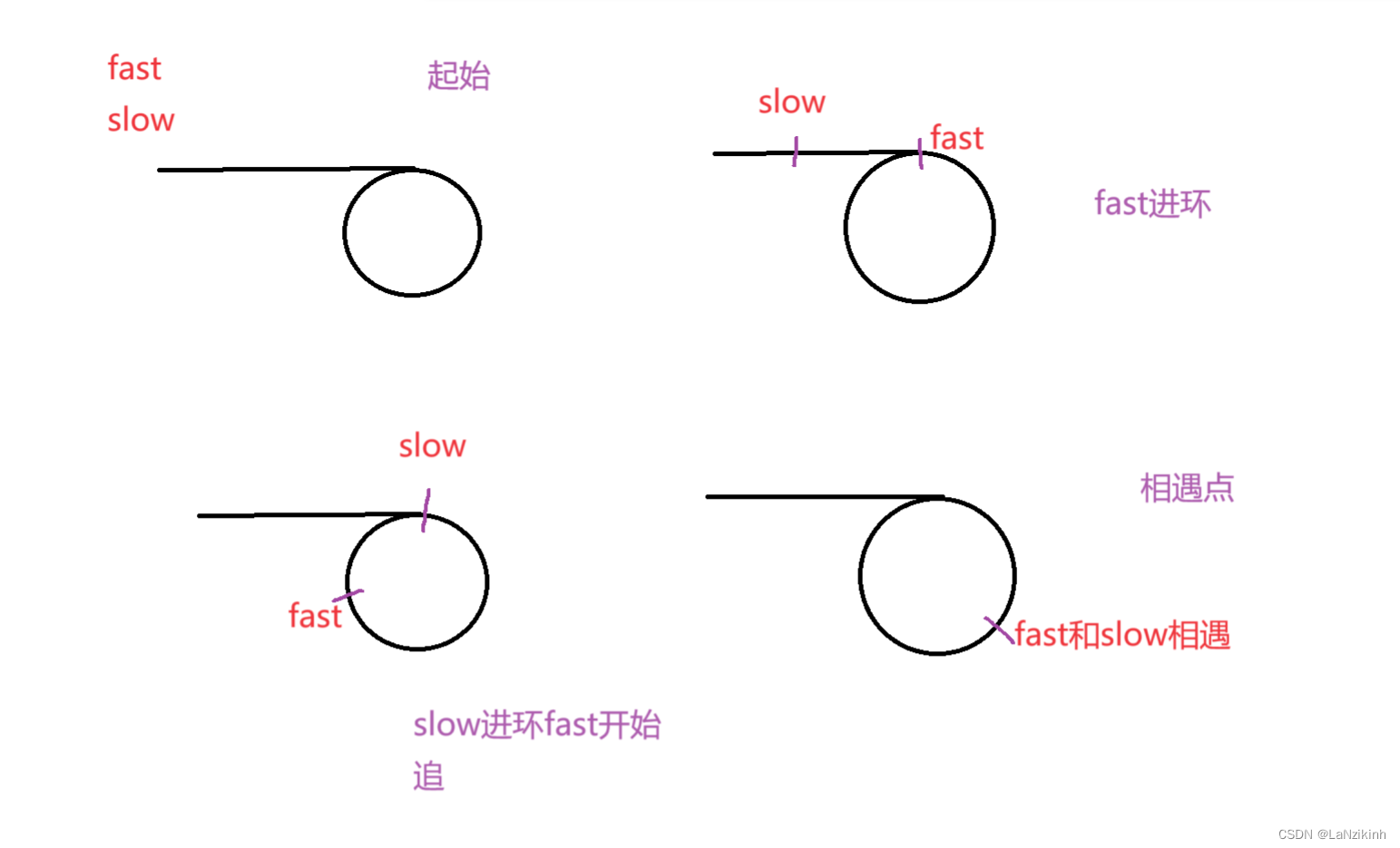

就是這4種情況，然后寫代碼就可以了，這個并不難 。

bool hasCycle(struct ListNode* head) 
{struct ListNode* slow = head, * fast = head;while (fast && fast->next)//存在奇偶{slow = slow->next;fast = fast->next->next;if (slow == fast)//相交就是環{return true;}}return false;
}

三.環形鏈表的延伸問題

1.為什么fast和slow一定會在環里相遇會不會在還里面錯過或者永遠追不上？

2.為什么一定是slow走一步fast走兩步？難道不能slow一步fast走其他步數？

3.如何去求入環口的節點呢？

3.1.為什么fast和slow一定會在環里相遇會不會在還里面錯過或者永遠追不上？

slow和fast一定是fast先入環，這時候slow走了入環前距離的一半，隨著slow進環，fast已經在環里走了一段距離了，走的多少和環的大小是有關系的，我們假設slow進環的時候離fast距離為N快的開始追慢的，慢的，每次走一步快的每次走兩步就相當于追y一步，所以說他的距離變化是N，N-1，N-2。。。1，0，他們之間的距離為零時就是相遇點，所以說一定追得上。

3.2為什么一定是slow走一步fast走兩步？難道不能slow一步fast走其他步數？

假設slow一步，fast3步，slow近環之后，他們的距離為N，則他們的距離變化為當N為偶數是N，N-2，N-4…..0，2。可以追得上，但是N為奇數的時候N的變化為N，N-2，N-4..1，-1。如果因為奇數距離為-1意味著他們之間的距離變成了c-1（c是環的長度），那么就要重新追，但是你重新追的話你就需要判斷c-1他是不是二的倍數，如果它是的話就可以追上不是的話就追不上。

在假設slow一步，fast4步，追3步，其實也是一樣的，如果N是3的倍數就可以追上，但是N不是3的倍數的話，就要看，有兩種情況，一種是N，N-3，N-6..2，-1。一種為N，N-3，N-6..1，-2。根據之前的結論，如c-1和c-2是3的倍數的話就可以追上

3.3如何去求入環口的節點呢？

先說結論:一個指針從相遇點開始走一個指針，從鏈表頭開始走，他們會在環的入口點相遇。

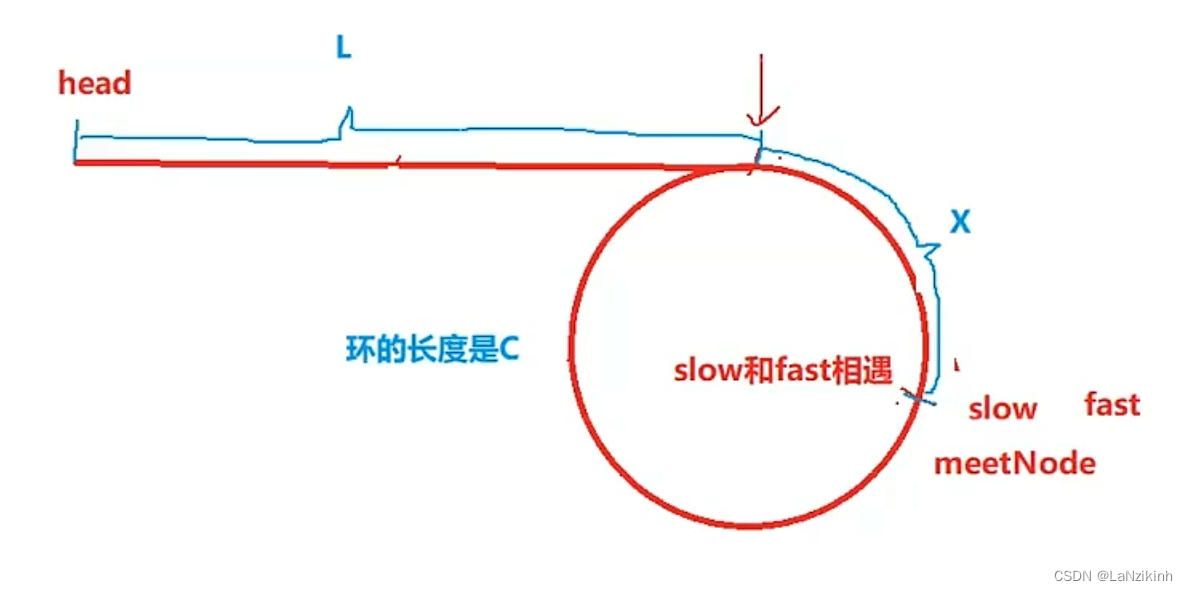
追上的相遇的過程中，慢指針的距離：L+X，快指針的距離：L+NC+X,因為你不知道fast在環里多跑了幾圈，所以設了一個N，但是N肯定>=1,又因為fast是slow的兩倍，所以2(L+X)=L+NC+X。整理可得L=(N-1)X+C-X，(N-1)X就是從meetNode開始又走到meetNode的距離，C-X就是從相遇點到入口點的距離，結論得證。

struct ListNode* deCycle(struct ListNode* head)
{struct ListNode* slow = head, * fast = head;while (fast && fast->next){slow = slow->next;fast = fast->next->next;//相遇了if (slow == fast){struct ListNode* meet = slow;//由公式得證while (meet != head){meet = meet->next;head = head->next;}return meet;}}return NULL;}

---

補充

其實求入口點還有一種方法就是在入口點處，直接指向空指針，把它看作一個相交鏈表來做，由頭節點和相遇點之前的那個節點，然后兩個節點找相交點就可以了。