CSGraph代表 壓縮稀疏圖 ，它著重于基于稀疏矩陣表示的快速圖算法。

圖表表示

首先，讓我們了解一個稀疏圖是什么以及它在圖表示中的作用。

什么是稀疏圖？

圖形只是節點的集合，它們之間有鏈接。圖表幾乎可以代表任何事物 - 社交網絡連接，每個節點都是一個人，并且與熟人相連;

圖像，其中每個節點是像素并連接到相鄰像素; 指向高維分布，其中每個節點都連接到最近的鄰居，并且幾乎可以想象其他任何事物。

表示圖形數據的一種非常有效的方式是在一個稀疏矩陣中：讓我們稱之為G.矩陣G的大小為N×N，并且G

[i，j]給出節點'i'和節點之間的連接的值'J'。稀疏圖形包含大部分零 - 也就是說，大多數節點只有幾個連接。在大多數感興趣的情況下，該屬性都是事實。

在scikit-learn中使用的幾種算法激發了稀疏圖子模塊的創建，其中包括以下內容 -

Isomap - 流形學習算法，需要在圖中找到最短路徑。

分層聚類 - 基于最小生成樹的聚類算法。

譜分解 - 基于稀疏圖拉普拉斯算子的投影算法。

作為一個具體的例子，假設我們想要表示以下無向圖 -

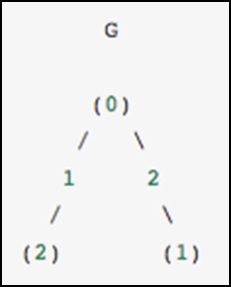
該圖有三個節點，其中節點0和1通過權重2的邊連接，節點0和2通過權重1的邊連接。我們可以構造如下例所示的稠密，蒙板和稀疏表示請記住，無向圖由對稱矩陣表示。

G_dense = np.array([ [0, 2, 1],

[2, 0, 0],

[1, 0, 0] ])

G_masked = np.ma.masked_values(G_dense, 0)

from scipy.sparse import csr_matrix

G_sparse = csr_matrix(G_dense)

print G_sparse.data

上述程序將生成以下輸出。

array([2, 1, 2, 1])

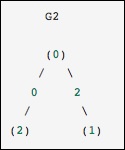
這與前面的圖相同，只是節點0和2通過零權重的邊連接。在這種情況下，上面的密集表示會導致含糊不清 -

如果零是一個有意義的值，那么如何表示非邊緣。在這種情況下，必須使用蒙版或稀疏表示來消除歧義。

讓我們考慮下面的例子。

from scipy.sparse.csgraph import csgraph_from_dense

G2_data = np.array

([

[np.inf, 2, 0 ],

[2, np.inf, np.inf],

[0, np.inf, np.inf]

])

G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)

print G2_sparse.data

上述程序將生成以下輸出。

array([ 2., 0., 2., 0.])