本文為『InfoQ x 蘇寧 2018雙十一』技術特別策劃系列文章之一。

1. 背景

隨著物聯網和人工智能的發展，越來越多的任務漸漸的被機器人取代，機器人逐漸在發展中慢慢進入物流領域，“智能叉車”，AGV（Automated Guided Vehicle，自主導航車）的出現不僅大大降低了人工成本，還在提升效率，面對海量訂單揀選時候有不錯的表現。在實際應用中，一個倉庫內多個AGV協作完成訂單是不可或缺的部分，而且多個AGV共同運輸的過程中同時進行路徑規劃需要一定的算法做支撐，本文在一個倉庫內多個AGV協作進行路徑規劃的方向上進行算法的研究，對其原理和實現進行分析和介紹。

2. 分析

首先，我們的背景設置在物流倉庫，針對倉庫中常見的入庫、揀貨、出庫等具體的任務細節進行分析，來了解我們AGV所面臨的場景。

傳統的方式一般采用靜止的貨架，入庫時將商品運輸到指定貨架前，人工上架入庫，揀貨時人工去到指定的貨架揀選訂單對應的商品打包出庫，引入AGV之后，模式將發生改變，我們會在倉庫規劃指定的入庫區、揀選區，AGV會將包含訂單的貨架動態地運輸到揀選區，排隊等待人工或者機械臂揀選到指定的訂單揀選筐內打包出庫，完成揀選后將貨架運輸至指定位置。

所以，引入AGV之后，我們面臨的問題是為了最大限度的提高效率，多個AGV如何避免擁堵和碰撞，如何對每個AGV規劃出更好的行走路線，怎樣才能讓每個AGV花最小的代價，完成更多的任務，將是此文討論的重點。

3. 問題拆解

要使得多個機器人在道路規劃上最優，無非是在單個小車規劃路徑時考慮其他小車的行駛路線，進而選取最優的一個行駛方案。另外，不同于室外場景，我們在倉庫中規劃小車路徑，整個道路都是可以設計的，所以我們的問題可拆解為：

(1)\t倉庫中道路的設計；
(2)\t獲取到其他小車的路徑行駛狀態；
(3)\t定義可能的道路擁堵；
(4)\t規劃最短路徑；
(5)\t交通管制。

3.1 倉庫中的道路設計

一些常見的道路設計如圖1和圖2，根據實際的應用場景來布局，考慮的因素包括倉庫的結構，商品的種類等，根據實際測試或模擬來選取最優的設計。

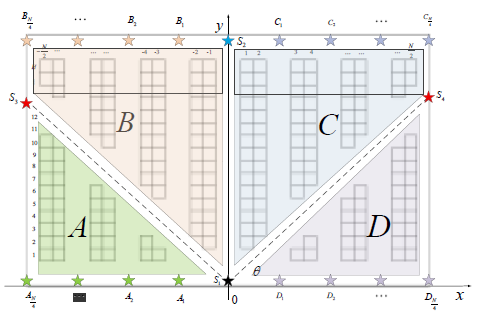
圖1. V字型道路設計

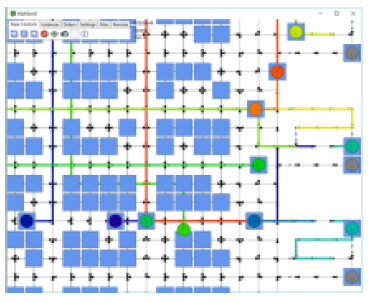
圖2. 井字型道路設計

3.2 獲取到其他小車的路徑行駛狀態

要做到全局路徑規劃，必須得到每一個時刻小車的位置和運行狀態，所以必須和小車建立起穩定的通信系統，一般采用無線局域網的方式，用TCP建立連接，選取合適的WIFI通道來保證小車和全局路徑規劃系統的通信的穩健。

3.3 定義可能的道路擁堵

在倉庫的道路規劃完成之后，首先要考慮的因素是可能的道路擁堵情況，一般小車在倉庫中都是直線行走，需要轉彎時要停在原地，原地旋轉90°或180°之后繼續直線行走，所以每個轉彎都有機會造成當前道路擁堵。另外，同一條道路車流量較大時，也會造成道路擁堵，加上路口會車的情況，主要造成道路擁堵的有轉彎、會車和車流量較大3種常見的可能情況。

3.4 規劃最短路徑

最短路徑規劃是全局路徑規劃的核心，要從地圖上的一個位置到達另一個位置，在中間有障礙物以及考慮到可能的道路擁堵情況，必須使用一個路徑搜索算法來尋找從初始點到目標點的一條最短路徑，常見的搜索路徑的算法有廣度優先算法、深度優先算法、Dijkstra算法、A*算法等，廣度優先算法和深度優先算法適用于樹形結構求解最短路徑或最小權重的場景，環狀結構求解最短路徑一般采用Dijkstra算法，A*算法是靜態路網中求解最短路徑最有效的直接搜索方法。

每一種算法都有其應用場景，對于我們全局路徑規劃的場景，我們的地圖更容易轉換成柵格地圖，而A*算法在柵格地圖上搜索最短路徑有明顯的優勢，而且方便于修改加上我們道路擁堵場景的考量，所以我們以A*算法為首選最短路徑算法，進而分析實現全局路徑規劃。

3.5 交通管制

交通管制主要應用于會車和并流場景，一方面為了避免車輛碰撞，另一方面路口會車比較常見，處理不好會導致車輛死鎖，車輛相互等待，進而導致任務無法完成，也是全局路徑規劃的核心算法，常見的會車場景如圖3。

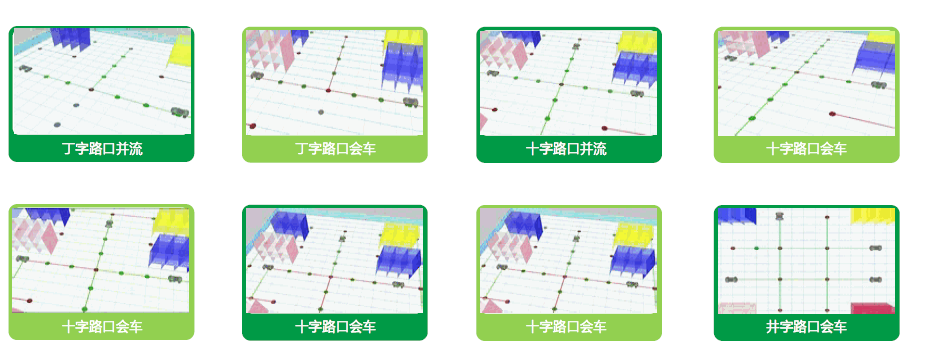
圖3. 路口會車

4. 核心算法實現

路徑規劃算法的核心主要在于最短路徑的規劃和交通管制，這里將對一種最短路徑規劃算法和交通管制算法進行算法剖析，進而設計出一套完整的全局路徑規劃算法。

4.1 A*算法規劃最短路徑

A*算法類似于圖論中尋找最優樹，通常是通盤考慮選擇某一路徑的路徑耗費，在所有可通過的路徑中總有一條路徑相對于其他任何可通行的路徑來說是耗費最少的。在圖論中尋找最佳路徑時每一條的路徑耗費是已知且固定的，但在用A*算法求解最佳路徑時，沿著不同的路徑前進，盡管是同一節點但其耗費可能是不同的，這便是啟發式尋路的精髓。

運用此方式時，首先將實際問題抽象出來，用矩陣的形式表示問題中的各元素，包括起點位置，目標點位置，以及出現的障礙物。我們會逐漸地發現在尋路方面都是將實際問題抽象地用矩陣表示，之后通過對矩陣的操作模擬實現尋路過程。

其基本思想是以起點為中心，其周圍緊鄰的8個點都通過指針指向它，在其周圍點內選擇最佳路徑點并以它為中心點將其還未建立指針聯系的周圍點（可行的，這在后文中解釋）通過指針指向它，并選擇最佳路徑點再以此點為中心尋路直到尋找到點的周圍點中有目標點，這樣尋找的路徑就通過指針一一連接起來了，最后通過輸出這些點就是尋找的路徑了。

下文主要通過以下幾個方面來逐步分析A*算法的尋路過程：

(1)\t將實際問題抽象化為矩陣表示

抽象出的矩陣如圖4，其中綠色區域表示起始點，紅色區域表示目標點，中間藍色區域表示障礙物（如不可通過的高山或是河流），黑色區域表示可產生路徑的區域。

(2)\t以起點為中心尋找到下一節點

如圖5所示，以起點為中心與之緊密相鄰的8個點是其所尋路徑上可到的下一點，且都以指針的形式將中間當前點作為與其緊鄰的周圍點的父節點。對于這8個點，應該選擇哪一點作為尋路的下一個起點呢，A*算法中建立了兩個列表，一個為開啟列表（用于存儲所有當前點的可到點（除去已經在關閉列表中的點、障礙物點）），另一個為關閉列表（里面存儲已經到過的點，已經在關閉列表中的點在下一次尋路的過程中是不會再次檢查的，這也說明尋路的線路不會有相交的可能）。

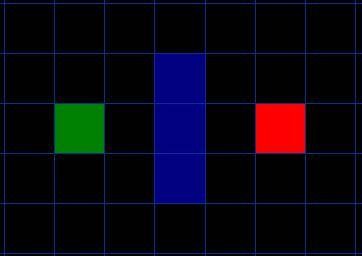
圖4

圖5

(3)\t選擇下一節點

將起點加入關閉列表，在以后的尋路過程中不再對其進行檢查，接下來就是在這8個點中選擇一個作為下一路徑點，選擇的原則是在其中尋找路徑耗費最小的節點，

其權值用F表示，F=G+H

其中G表示從起點開始，沿著產生的路徑，移動到指定方格上的路徑耗費；如圖6所示，以起點為中心其緊鄰周圍點有上下左右、對角線方向上的8個點，以上下左右移動路徑耗費為10，對角線耗費為 $ \\sqrt{2} \\times10$，約為14。

其中H表示從路徑所在的當前點到終點的移動路徑耗費，計算方法為當前點到目的點之間水平和垂直的方格的數量總和，然后把結果乘以10。

從圖7可以看出，起始點右邊點的權值F最小，故將其作為下一路徑點。

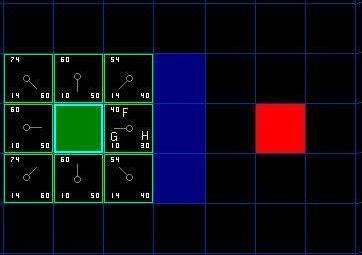
圖6

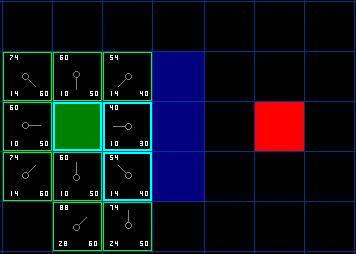
圖7

(4)\t繼續搜索

把路徑點從開啟列表中刪除，并添加到關閉列表中。檢查與此點緊鄰的8個點（忽略在關閉列表中或者不可通過的點），把他們添加進開啟列表，如果存在還有點沒有添加進開啟列表，則將路徑點作為此類點的父節點并添加進開啟列表。

如果所有可行的緊鄰點已經在開啟列表中，對每一緊鄰點檢查目前這條路徑到是否比上一路徑點到這一緊鄰點的路徑耗費要小，如果不是則什么都不用做（如圖8所示）從原始起點到其緊鄰的右下方的點，按照新產生路徑G值：G1=10+10=20，而原始路徑G值G2=14，即新產生路徑的G值比原始路徑的G值大，而它們的H值相同（為同一點）故原始路徑的F值比新產生路徑的F值要小，不做任何處理，繼續下一步尋路。如果是，那就把相鄰方格的父節點改為目前選中的方格，說明新產生的路徑的移動耗費更小。

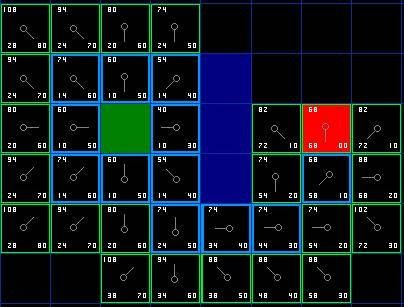
圖8

(5)\t重復上一搜索過程直至結束

搜尋過程結束分為兩種情況：一種是目標點加入關閉列表，搜索正常結束，找到路徑。另一種情況是目標點未找到但開啟列表已經為空，意味著沒有找到從起始點到目標點的路徑，搜索結束。

搜索過程如圖9所示，從中可以看出從起點到目標點之間有指針指向一致的一條路徑，這便A*算法是搜尋到的路徑。在路徑點上添加紅色點突出顯示，此即為從起始點到終點的一條路徑。

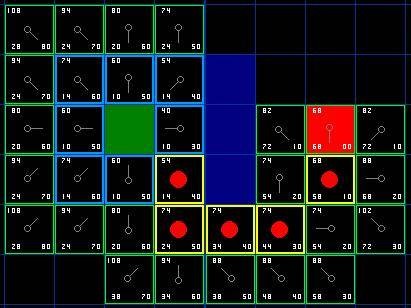
圖9

整個尋路過程整理如下：

1. 起始格加入開啟列表；
2. 重復如下的工作：
   a. 尋找開啟列表中F值最低的點。我們稱它為當前點；
   b. 把它加入關閉列表；
   c. 對緊鄰的8格中的每一點
   • 如果它不可通過或者已經在關閉列表中，略過它。反之如下：
   • 如果它不在開啟列表中，把它添加進去。把當前點作為這一格的父節點。記錄這一點的F、G和H值；
   • 如果它已經在開啟列表中，用G值為參考檢查新的路徑是否更好。更低的G值意味著更好的路徑。如果是這樣，就把這一點的父節 點改成當前點，并且重新計算這一點的G和F值。改變之后需要重新對開啟列表按F值大小排序。如果不是則不需要做后面改變指針指向并重新計算G、F值的工作；
3. 停止搜索，分為兩種情況：
   • 當目標點添加入了關閉列表，這時候路徑被找到，搜索正常結束；
   • 沒有找到目標點，但開啟列表已經空了，此時未找到合適的路徑，搜索結束；
4. 保存路徑。從目標點開始，沿著每一點的指針指向移動，直到回到起始點，輸出路徑。

4.2 基于鎖格機制的交通管制

車輛道路規劃完成后，多個小車同時開始行走，多條道路小車會車的情況不可避免，會車時候車輛主要會出現跟隨，相向而行，十字路口或丁字路口的情況，跟隨的時候車輛前方會有傳感器避免跟隨碰撞，為了避免十字路和丁字路會車碰撞，會車時候采取鎖格的方式，即：

(1)\t每輛小車行走一步，將前面即將行走的兩步的點鎖住；
(2)\t小車鎖格時發現即將鎖的地圖的點已經被鎖住，則兩車協商看哪個優先級高，哪輛車先行，另一輛車停車等待；
(3)\t小車走過之后將解鎖，等待的時候可以重新鎖住即將行駛的點，繼續往前行走；
(4)\t循環一直每一步都進行鎖格操作。

4.3 全局路徑規劃

在規劃當前小車路徑時，要在考慮到道路擁堵的情況下去規劃最短路徑，以滿足整體規劃結果最優，使用A*算法，用G值為參考檢查新的路徑是否更好， 將地圖中其他小車規劃的路徑的點的G值增加，即可盡量避免搜索到相同的路徑，同樣的道理，在車輛需要轉彎的時候，也同樣增加轉彎下一點的G值，從而規劃路徑盡量避免轉彎的情況出現，來達到整體效率最高，全局路徑最優。
此外，由于路徑規劃都是靜態規劃的路徑，車輛在行走過程中同時需要對每輛小車進行鎖格的交通管制，來保證車輛不會相撞。

5. 總結

本文主要對倉庫內多AGV協作的全局路徑規劃進行了研究，并介紹了一種可能的實現算法方案，從倉庫中道路的設計，擁堵的考量等角度簡單全局路徑規劃需要考慮的維度，對最短路徑規劃和交通管制策略進行的詳細的分析和應用設計。

作者：董效成，蘇寧易購IT總部人工智能研發中心技術經理，負責機器人項目任務匹配和路徑規劃算法工作。有多年的機器人算法開發經驗，對輪式機器人的運動控制，路徑規劃等算法有深刻的理解，有豐富的機器人操作系統（ROS）開發實踐經驗。