神經網絡的基本工作原理

神經網絡的基本工作原理

一、總結

一句話總結：先給一個初始值，然后依賴正確值（真實值）進行修復模型（訓練模型），直到模型和真實值的誤差可接受

初始值 真實值 修復模型

?

1、神經網絡由基本的神經元組成，那么神經元的模型是怎樣的？

神經網絡由基本的神經元組成，下圖就是一個神經元的數學/計算模型，便于我們用程序來實現。

輸入

(x1,x2,x3) 是外界輸入信號，一般是一個訓練數據樣本的多個屬性，比如，我們要識別手寫數字0~9，那么在手寫圖片樣本中，x1可能代表了筆畫是直的還是有彎曲，x2可能代表筆畫所占面積的寬度，x3可能代表筆畫上下兩部分的復雜度。

(W1,W2,W3) 是每個輸入信號的權重值，以上面的 (x1,x2,x3) 的例子來說，x1的權重可能是0.5，x2的權重可能是0.2，x3的權重可能是0.3。當然權重值相加之后可以不是1。

還有個b是干嗎的？一般的書或者博客上會告訴你那是因為\(y=wx+b\)，b是偏移值，使得直線能夠沿Y軸上下移動。這是用結果來解釋原因，并非b存在的真實原因。從生物學上解釋，在腦神經細胞中，一定是輸入信號的電平/電流大于某個臨界值時，神經元細胞才會處于興奮狀態，這個b實際就是那個臨界值。亦即當：

\[w1*x1 + w2*x2 + w3*x3 >= t\]

時，該神經元細胞才會興奮。我們把t挪到等式左側來，變成\((-t)\)，然后把它寫成b，變成了：

\[w1*x1 + w2*x2 + w3*x3 + b >= 0\]

于是b誕生了！

?

2、神經元模型中的偏移b到底是什么？

偏移量 興奮 臨界值

一般的書或者博客上會告訴你那是因為\(y=wx+b\)，b是偏移值，使得直線能夠沿Y軸上下移動。這是用結果來解釋原因，并非b存在的真實原因。從生物學上解釋，在腦神經細胞中，一定是輸入信號的電平/電流大于某個臨界值時，神經元細胞才會處于興奮狀態，這個b實際就是那個臨界值。亦即當：

\[w1*x1 + w2*x2 + w3*x3 >= t\]

時，該神經元細胞才會興奮。我們把t挪到等式左側來，變成\((-t)\)，然后把它寫成b，變成了：

\[w1*x1 + w2*x2 + w3*x3 + b >= 0\]

于是b誕生了！

?

3、神經元模型中的輸入代表什么意思？

問題 決定要素

具體要解決問題的決定要素

(x1,x2,x3) 是外界輸入信號，一般是一個訓練數據樣本的多個屬性，比如，我們要識別手寫數字0~9，那么在手寫圖片樣本中，x1可能代表了筆畫是直的還是有彎曲，x2可能代表筆畫所占面積的寬度，x3可能代表筆畫上下兩部分的復雜度。

(W1,W2,W3) 是每個輸入信號的權重值，以上面的 (x1,x2,x3) 的例子來說，x1的權重可能是0.5，x2的權重可能是0.2，x3的權重可能是0.3。當然權重值相加之后可以不是1。

?

4、為什么需要激活函數，為什么神經細胞需要處于激活狀態？

傳遞信號

求和之后，神經細胞已經處于興奮狀態了，已經決定要向下一個神經元傳遞信號了，但是要傳遞多強烈的信號，要由激活函數來確定：

\[A=\sigma{(Z)}\]

如果激活函數是一個階躍信號的話，那受不了啊，你會覺得腦子里總是一跳一跳的，像繼電器開合一樣咔咔亂響，所以一般激活函數都是有一個漸變的過程，也就是說是個曲線。

?

5、為什么激活函數是個曲線（漸變過程）？

漸變

如果激活函數是一個階躍信號的話，那受不了啊，你會覺得腦子里總是一跳一跳的，像繼電器開合一樣咔咔亂響，所以一般激活函數都是有一個漸變的過程，也就是說是個曲線。

?

6、神經網絡訓練流程是怎樣的？

初始值 真實值 修復模型

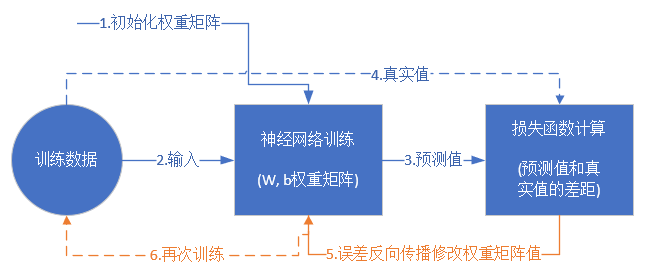
先給一個初始值，然后依賴正確值進行修復模型（訓練模型），直到模型和真實值的誤差可接受

?

7、神經網絡為什么能普遍適用？

單層 直線 兩層 任意函數

單層的神經網絡能夠模擬一條二維平面上的直線，從而可以完成線性分割任務。而理論證明，兩層神經網絡可以無限逼近任意連續函數。

比如下面這張圖，二維平面中有兩類點，紅色的和藍色的，用一條直線肯定不能把兩者分開了。

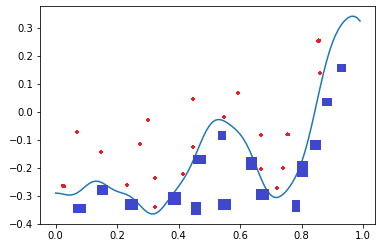
我們使用一個兩層的神經網絡可以得到一個非常近似的結果，使得分類誤差在滿意的范圍之內。而這個真實的連續函數的原型是：

\[y=0.4x^2 + 0.3xsin(15x) + 0.01cos(50x)-0.3\]

哦，my god（我靠）! 這么復雜的函數，一個兩層的神經網絡是如何做到的呢？其實從輸入層到隱藏層的矩陣計算，就是對輸入數據進行了空間變換，使其可以被線性可分，然后輸出層畫出了一個分界線。而訓練的過程，就是確定那個空間變換矩陣的過程。因此，多層神經網絡的本質就是對復雜函數的擬合。我們可以在后面的試驗中來學習如何擬合上述的復雜函數的。

?

8、為什么我們不能在沒有激活輸入信號的情況下完成神經網絡的學習呢？

線性函數 線性回歸模型

復雜功能

如果我們不運用激活函數的話，則輸出信號將僅僅是一個簡單的線性函數。線性函數一個一級多項式。現如今，線性方程是很容易解決的，但是它們的復雜性有限，并且從數據中學習復雜函數映射的能力更小。一個沒有激活函數的神經網絡將只不過是一個線性回歸模型（Linear regression Model）罷了，它功率有限，并且大多數情況下執行得并不好。我們希望我們的神經網絡不僅僅可以學習和計算線性函數，而且還要比這復雜得多。同樣是因為沒有激活函數，我們的神經網絡將無法學習和模擬其他復雜類型的數據，例如圖像、視頻、音頻、語音等。這就是為什么我們要使用人工神經網絡技術，諸如深度學習（Deep learning），來理解一些復雜的事情，一些相互之間具有很多隱藏層的非線性問題，而這也可以幫助我們了解復雜的數據。

?

9、神經網絡中為什么我們需要非線性函數？

需求 任意

非線性函數是那些一級以上的函數，而且當繪制非線性函數時它們具有曲率。現在我們需要一個可以學習和表示幾乎任何東西的神經網絡模型，以及可以將輸入映射到輸出的任意復雜函數。神經網絡被認為是通用函數近似器（Universal Function Approximators）。這意味著他們可以計算和學習任何函數。幾乎我們可以想到的任何過程都可以表示為神經網絡中的函數計算。
而這一切都歸結于這一點，我們需要應用激活函數f（x），以便使網絡更加強大，增加它的能力，使它可以學習復雜的事物，復雜的表單數據，以及表示輸入輸出之間非線性的復雜的任意函數映射。因此，使用非線性激活函數，我們便能夠從輸入輸出之間生成非線性映射。
激活函數的另一個重要特征是：它應該是可以區分的。我們需要這樣做，以便在網絡中向后推進以計算相對于權重的誤差（丟失）梯度時執行反向優化策略，然后相應地使用梯度下降或任何其他優化技術優化權重以減少誤差。

?

10、深度神經網絡與深度學習？

神經元 數量

層 數量

兩層的神經網絡雖然強大，但可能只能完成二維空間上的一些曲線擬合的事情。如果對于圖片、語音、文字序列這些復雜的事情，就需要更復雜的網絡來理解和處理。第一個方式是增加每一層中神經元的數量，但這是線性的，不夠有效。另外一個方式是增加層的數量，每一層都處理不同的事情。

淺神經網絡雖然具備了反向傳播機制，但是仍存在問題：

1. 梯度越來越疏，從后向前，誤差校正信號越來越微弱
2. 隨機初始化會導致訓練過程收斂到局部最小值
3. 需要數據帶標簽(人工label好的數據)，但是大部分數據沒標簽

?

11、Deep Learning的訓練過程簡介？

自下上升 非監督學習

自頂向下 監督學習

使用自下上升非監督學習（就是從底層開始，一層一層的往頂層訓練）

自頂向下的監督學習（就是通過帶標簽的數據去訓練，誤差自頂向下傳輸，對網絡進行微調）

?

?

?

?

二、神經網絡的基本工作原理（轉）

轉自：神經網絡的基本工作原理 - UniversalAIPlatform - 博客園
https://www.cnblogs.com/ms-uap/p/9928254.html

看過很多博客、文章，東一榔頭西一棒子的，總覺得沒有一個系列的文章把問題從頭到尾說清楚，找東西很困難。有的博客、文章的質量還不算很理想，似是而非，或者重點不明確，或者直接把別人的博客抄襲過來......種種不靠譜，讓小白們學習起來很困難，增加了學習曲線的陡峭程度。當然也有很多博主非常非常負責任，文章質量很高，只是連續度不夠，正看得過癮的時候，沒有后續章節了。

從本文開始，我們試圖用一系列博客，講解現代神經網絡的基本知識，使大家能夠從真正的“零”開始，對神經網絡、深度學習有基本的了解，并能動手實踐。這是本系列的第一篇，我們先從神經網絡的基本工作原理開始講解。

神經元細胞的數學計算模型

神經網絡由基本的神經元組成，下圖就是一個神經元的數學/計算模型，便于我們用程序來實現。

輸入

(x1,x2,x3) 是外界輸入信號，一般是一個訓練數據樣本的多個屬性，比如，我們要識別手寫數字0~9，那么在手寫圖片樣本中，x1可能代表了筆畫是直的還是有彎曲，x2可能代表筆畫所占面積的寬度，x3可能代表筆畫上下兩部分的復雜度。

(W1,W2,W3) 是每個輸入信號的權重值，以上面的 (x1,x2,x3) 的例子來說，x1的權重可能是0.5，x2的權重可能是0.2，x3的權重可能是0.3。當然權重值相加之后可以不是1。

還有個b是干嗎的？一般的書或者博客上會告訴你那是因為\(y=wx+b\)，b是偏移值，使得直線能夠沿Y軸上下移動。這是用結果來解釋原因，并非b存在的真實原因。從生物學上解釋，在腦神經細胞中，一定是輸入信號的電平/電流大于某個臨界值時，神經元細胞才會處于興奮狀態，這個b實際就是那個臨界值。亦即當：

\[w1*x1 + w2*x2 + w3*x3 >= t\]

時，該神經元細胞才會興奮。我們把t挪到等式左側來，變成\((-t)\)，然后把它寫成b，變成了：

\[w1*x1 + w2*x2 + w3*x3 + b >= 0\]

于是b誕生了！

求和計算

\[Z = w1*x1 + w2*x2 + w3*x3 + b = \sum_{i=1}^m(w_i*x_i) + b\]

在上面的例子中m=3。我們把\(w_i*x_i\)變成矩陣運算的話，就變成了：

\[Z = W*X + b\]

激活函數

求和之后，神經細胞已經處于興奮狀態了，已經決定要向下一個神經元傳遞信號了，但是要傳遞多強烈的信號，要由激活函數來確定：

\[A=\sigma{(Z)}\]

如果激活函數是一個階躍信號的話，那受不了啊，你會覺得腦子里總是一跳一跳的，像繼電器開合一樣咔咔亂響，所以一般激活函數都是有一個漸變的過程，也就是說是個曲線。

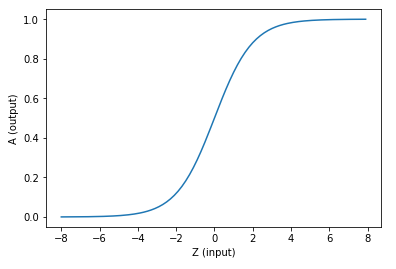
激活函數的更多描述在后續的博客中。

至此，一個神經元的工作過程就在電光火石般的一瞬間結束了。

神經網絡的基本訓練過程

單層神經網絡模型

這是一個單層的神經網絡，有m個輸入 (這里m=3)，有n個輸出 (這里n=2)。在單個神經元里，b是個值。但是在神經網絡中，我們把b的值永遠設置為1，而用b到每個神經元的權值來表示實際的偏移值，亦即(b1,b2)，這樣便于矩陣運算。也有些作者把b寫成x0，其實是同一個意思，只不過x0用于等于1。

• (x1,x2,x3)是一個樣本數據的三個特征值
• (w11,w12,w13)是(x1,x2,x3)到n1的權重
• (w21,w22,w23)是(x1,x2,x3)到n2的權重
• b1是n1的偏移
• b2是n2的偏移

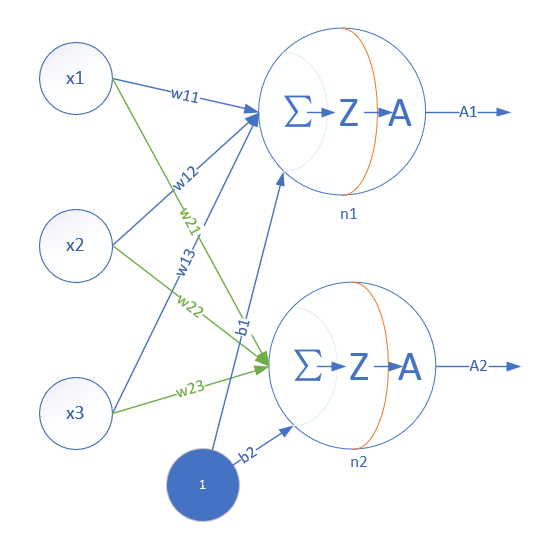
從這里大家可以意識到，同一個特征x1，對于n1、n2來說，權重是不相同的，因為n1、n2是兩個神經元，它們完成不同的任務（特征識別）。這就如同老師講同樣的課，不同的學生有不同的理解。

而對于n1來說，x1，x2，x3輸入的權重也是不相同的，因為它要對不同特征有選擇地接納。這就如同一個學生上三門課，但是側重點不同，第一門課花50%的精力，第二門課30%，第三門課20%。

訓練流程

從真正的“零”開始學習神經網絡時，我沒有看到過一個流程圖來講述訓練過程，大神們寫書或者博客時都忽略了這一點，我在這里給大家畫一個簡單的流程圖：

損失函數和反向傳播的更多內容在后續的博客中。

前提條件

1. 首先是我們已經有了訓練數據，否則連目標都沒有，訓練個啥？
2. 我們已經根據數據的規模、領域，建立了神經網絡的基本結構，比如有幾層，每一層有幾個神經元
3. 定義好損失函數來合理地計算誤差

步驟

假設我們有以下訓練數據樣本：

Id	x1	x2	x3	Y
1	0.5	1.4	2.7	3
2	0.4	1.3	2.5	5
3	0.1	1.5	2.3	9
4	0.5	1.7	2.9	1

其中，x1，x2，x3是每一個樣本數據的三個特征值，Y是樣本的真實結果值，

1. 隨機初始化權重矩陣，可以根據高斯分布或者正態分布等來初始化。這一步可以叫做“蒙”，但不是瞎蒙。
2. 拿一個或一批數據作為輸入，帶入權重矩陣中計算，再通過激活函數傳入下一層，最終得到預測值。在本例中，我們先用Id-1的數據輸入到矩陣中，得到一個A值，假設A=5
3. 拿到Id-1樣本的真實值Y=3
4. 計算損失，假設用均方差函數 \(Loss = (A-Y)^2=(5-3)^2=4\)
5. 根據一些神奇的數學公式（反向微分），把Loss=4這個值用大喇叭喊話，告訴在前面計算的步驟中，影響A=5這個值的每一個權重矩陣，然后對這些權重矩陣中的值做一個微小的修改（當然是向著好的方向修改，這一點可以用數學家的名譽來保證）
6. 用Id-2樣本作為輸入再次訓練（goto 2）
7. 這樣不斷地迭代下去，直到以下一個或幾個條件滿足就停止訓練：損失函數值非常小；迭代了指定的次數；計算機累吐血了......

訓練完成后，我們會把這個神經網絡中的結構和權重矩陣的值導出來，形成一個計算圖（就是矩陣運算加上激活函數）模型，然后嵌入到任何可以識別/調用這個模型的應用程序中，根據輸入的值進行運算，輸出預測值。

神經網絡中的矩陣運算

下面這個圖就是一個兩層的神經網絡，包含隱藏層和輸出層：

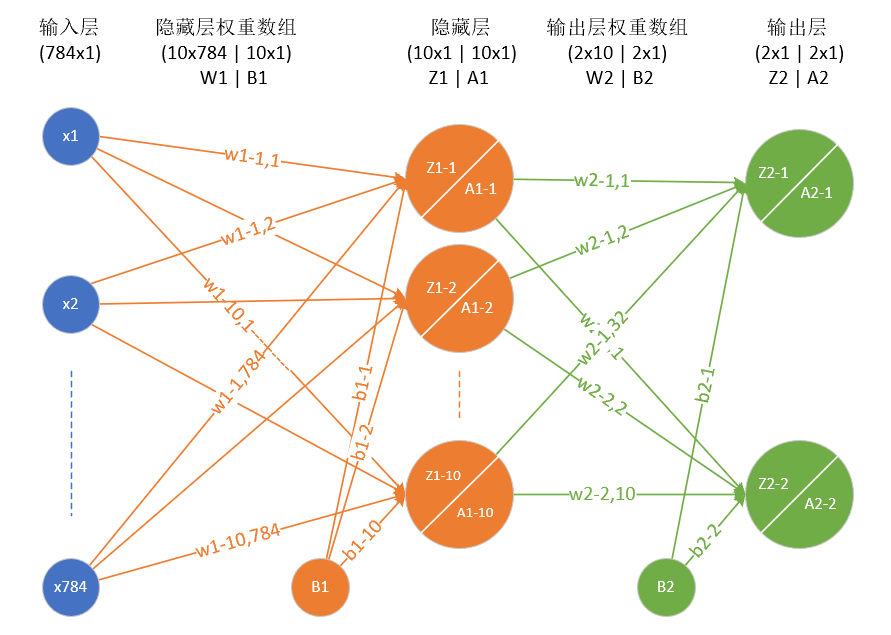
其中，w1-m,n（應該寫作\(w^1_{1,1},w^1_{1,2},w^1_{1,3}\)，上面的角標1表示第1層，但是visio里不支持這種格式）表示第一層神經網絡的權重矩陣，w2-m,n（應該寫作\(w^2_{1,1},w^2_{1,2},w^2_{1,3}\)）表示第二層神經網絡的權重矩陣。

\[Z^1_1 = w^1_{1,1}x_1+w^1_{1,2}x_2+w^1_{1,784}x_{784}+b_1^1\\ ......\\ Z^1_{10} = w^1_{10,1}x_1+w^1_{10,2}x_2+w^1_{10,784}x_{784}+b_{10}^{1}\]

變成矩陣運算：

\[ Z_1^1=\begin{pmatrix}w^1_{1,1}&w^1_{1,2}&...&w^1_{1,784}\end{pmatrix} \begin{pmatrix}x_1\\x_2\\...\\x_{784}\end{pmatrix} +b^1_1\\ .....\\ Z_{10}^1= \begin{pmatrix}w^1_{10,1}&w^1_{10,2}&...&w^1_{10,784}\end{pmatrix} \begin{pmatrix}x_1\\x_2\\...\\x_{784}\end{pmatrix} +b^1_{10} \]

再變成大矩陣：

\[Z_1 = \begin{pmatrix} w^1_{1,1}&w^1_{1,2}&...&w^1_{1,784} \\ w^1_{2,1}&w^1_{2,2}&...&w^1_{2,784}\\ ......\\ w^1_{10,1}&w^1_{10,2}&...&w^1_{10,784} \end{pmatrix} \begin{pmatrix}x_1\\x_2\\...\\x_{784}\end{pmatrix} +\begin{pmatrix}b^1_1\\b^1_2\\...\\ b^1_{10} \end{pmatrix}\]

最后變成矩陣符號：

\[Z_1 = W_1X + B_1\]

然后是激活函數運算：

\[A_1=\sigma{(Z_1)}\]

同理可得：

\[Z_2 = W_2A_1 + B_2\]
\[A_2=\sigma{(Z_2)}\]

神經網絡為什么能普遍適用

單層的神經網絡能夠模擬一條二維平面上的直線，從而可以完成線性分割任務。而理論證明，兩層神經網絡可以無限逼近任意連續函數。

比如下面這張圖，二維平面中有兩類點，紅色的和藍色的，用一條直線肯定不能把兩者分開了。

我們使用一個兩層的神經網絡可以得到一個非常近似的結果，使得分類誤差在滿意的范圍之內。而這個真實的連續函數的原型是：

\[y=0.4x^2 + 0.3xsin(15x) + 0.01cos(50x)-0.3\]

哦，my god（我靠）! 這么復雜的函數，一個兩層的神經網絡是如何做到的呢？其實從輸入層到隱藏層的矩陣計算，就是對輸入數據進行了空間變換，使其可以被線性可分，然后輸出層畫出了一個分界線。而訓練的過程，就是確定那個空間變換矩陣的過程。因此，多層神經網絡的本質就是對復雜函數的擬合。我們可以在后面的試驗中來學習如何擬合上述的復雜函數的。

為什么需要激活函數

為什么我們不能在沒有激活輸入信號的情況下完成神經網絡的學習呢？

如果我們不運用激活函數的話，則輸出信號將僅僅是一個簡單的線性函數。線性函數一個一級多項式。現如今，線性方程是很容易解決的，但是它們的復雜性有限，并且從數據中學習復雜函數映射的能力更小。一個沒有激活函數的神經網絡將只不過是一個線性回歸模型（Linear regression Model）罷了，它功率有限，并且大多數情況下執行得并不好。我們希望我們的神經網絡不僅僅可以學習和計算線性函數，而且還要比這復雜得多。同樣是因為沒有激活函數，我們的神經網絡將無法學習和模擬其他復雜類型的數據，例如圖像、視頻、音頻、語音等。這就是為什么我們要使用人工神經網絡技術，諸如深度學習（Deep learning），來理解一些復雜的事情，一些相互之間具有很多隱藏層的非線性問題，而這也可以幫助我們了解復雜的數據。

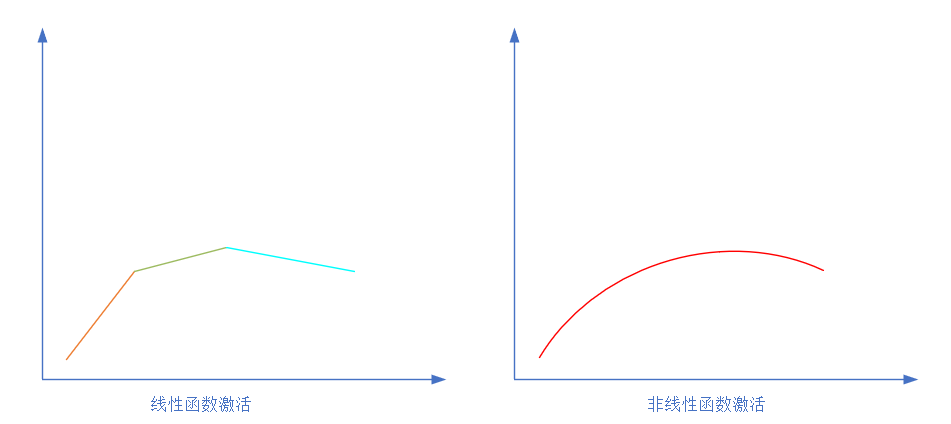
那么為什么我們需要非線性函數？

非線性函數是那些一級以上的函數，而且當繪制非線性函數時它們具有曲率。現在我們需要一個可以學習和表示幾乎任何東西的神經網絡模型，以及可以將輸入映射到輸出的任意復雜函數。神經網絡被認為是通用函數近似器（Universal Function Approximators）。這意味著他們可以計算和學習任何函數。幾乎我們可以想到的任何過程都可以表示為神經網絡中的函數計算。
而這一切都歸結于這一點，我們需要應用激活函數f（x），以便使網絡更加強大，增加它的能力，使它可以學習復雜的事物，復雜的表單數據，以及表示輸入輸出之間非線性的復雜的任意函數映射。因此，使用非線性激活函數，我們便能夠從輸入輸出之間生成非線性映射。
激活函數的另一個重要特征是：它應該是可以區分的。我們需要這樣做，以便在網絡中向后推進以計算相對于權重的誤差（丟失）梯度時執行反向優化策略，然后相應地使用梯度下降或任何其他優化技術優化權重以減少誤差。

深度神經網絡與深度學習

兩層的神經網絡雖然強大，但可能只能完成二維空間上的一些曲線擬合的事情。如果對于圖片、語音、文字序列這些復雜的事情，就需要更復雜的網絡來理解和處理。第一個方式是增加每一層中神經元的數量，但這是線性的，不夠有效。另外一個方式是增加層的數量，每一層都處理不同的事情。

淺神經網絡雖然具備了反向傳播機制，但是仍存在問題：

1. 梯度越來越疏，從后向前，誤差校正信號越來越微弱
2. 隨機初始化會導致訓練過程收斂到局部最小值
3. 需要數據帶標簽(人工label好的數據)，但是大部分數據沒標簽

Deep Learning的訓練過程簡介

1. 使用自下上升非監督學習（就是從底層開始，一層一層的往頂層訓練）：

   采用無標簽數據（有標簽數據也可）分層訓練各層參數，這一步可以看作是一個無監督訓練過程，是和傳統神經網絡區別最大的部分（這個過程可以看作是feature learning過程）。
   具體的，先用無標定數據訓練第一層，訓練時先學習第一層的參數（這一層可以看作是得到一個使得輸出和輸入差別最小的三層神經網絡的隱層），由于模型capacity的限制以及稀疏性約束，使得得到的模型能夠學習到數據本身的結構，從而得到比輸入更具有表示能力的特征；在學習得到第n-1層后，將n-1層的輸出作為第n層的輸入，訓練第n層，由此分別得到各層的參數；

2. 自頂向下的監督學習（就是通過帶標簽的數據去訓練，誤差自頂向下傳輸，對網絡進行微調）：

   基于第一步得到的各層參數進一步fine-tune整個多層模型的參數，這一步是一個有監督訓練過程；第一步類似神經網絡的隨機初始化初值過程，由于DL的第一步不是隨機初始化，而是通過學習輸入數據的結構得到的，因而這個初值更接近全局最優，從而能夠取得更好的效果；所以deep learning效果好很大程度上歸功于第一步的feature learning過程。