上面這個現象呢，是男生上廁所時的一種微妙狀態。兩個男生往往會由于尷尬而不愿意站在相鄰的坑位上廁所。我將其命名為男廁所的泡利不相容定律。

一、男廁尷尬定律簡介

先給大家科普一下男廁所的構造，小便區是一排立式坑位。好的廁所有隔板，阻擋隔壁視線，營造私密空間，但更多的情況是這樣的。

所以男生通常會離其他人盡可能遠。

這也合理，社會學研究表明，人的社交距離分四級：親密、熟人、禮貌、一般。親密距離是0-45cm，情侶之間才會離這么近。

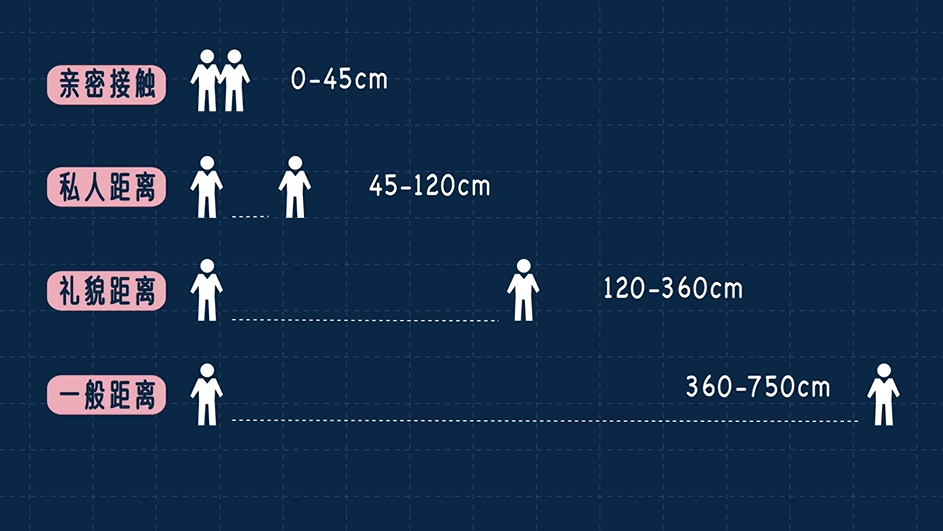
兩個男生萍水相逢，卻在親密距離內做親密之事，難免有些哈茲卡西。

如果不說點什么，尿聲無法掩蓋；如果旁邊人盯著你，你會很不自在；如果互相攀比尿液動力學，又有一點變態。有同感的話請在評論里打尷尬。

但這時你會發現一個問題！男生的尷尬心態導致了男廁所坑位利用率顯著降低！

考察一個4坑位廁所，第1個人進來占據1號坑，第2個人占據最遠的4號坑，第3個人進來就無坑可占了，因為兩邊都有人。

考察7坑位廁所，第1個人進來占據1號坑，第2個人占據7號坑，第3個人占據4號坑，第4個人進來又沒法上了！7個坑位只能容納3個人！

同理易得，13個坑位的廁所其實只能容納5個人！男生的一點面子竟然造成了社會資源極大的浪費！

順帶一說，后來在SCP基金會官網上我竟然看到了類似的記錄，據說是一種超自然現象，目前仍無法進行完全收容。

因此不一定是廣大男同胞面子薄，可能是你受到了超自然的影響。

想到這里我不禁陷入沉思。一個廁所的坑位數量和它能容納的男生人數滿足什么關系呢？最優秀的廁所應該設置多少個坑位，才能避免客人尷尬呢？

作為SNP大一統理論創始人，今天我就來和大家計算一下，男廁尷尬定理。

二、簡單計算

基本模型如下：

試求該廁所可同時容納的男生數量m與n的關系，記為m=f(n)。下面我們來給出一些合理的假設。

男廁第一定律，又稱就近定律：第1個男生為了圖方便，總是進入1號坑位。

男廁第二定律，又稱尷尬定律：與女生不同，男生從不結伴，總是獨立進入廁所，后來的男生總會選擇離左右男生盡可能遠的坑位。

男廁第三定律，又稱泡利不相容定律：男生永遠不挨著上廁所。

下面計算f(n)。做對的同學請在評論里打簡單。我來提供一個求解思路。

如果n是奇數，第1個人進入1號坑，第2個人進入n號坑，第3個人進入正中間的(n+1)/2號坑。這時左邊這(n+1)/2個坑能容納多少人呢？

不知道，但總之就是f((n+1)/2)個人。右邊這(n+1)/2個坑能容納多少人呢？也是f((n+1)/2)個人。現在我們雖然求不出f(n)，但我們知道了，

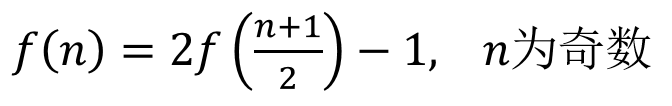
減1是因為要扣掉中間這個重復的人

如果n是偶數，則第1個人進入1號坑，第2個人進入n號坑，第3個人進入正中間的n/2號坑。這時左邊這n/2個坑能容納多少人呢？

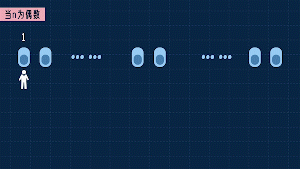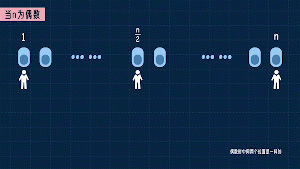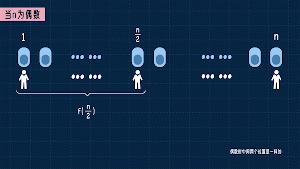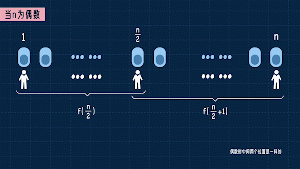
不知道，但總之是f(n/2)個人。右邊這(n/2+1)個坑能容納多少人呢？f(n/2+1)個人。所以這時

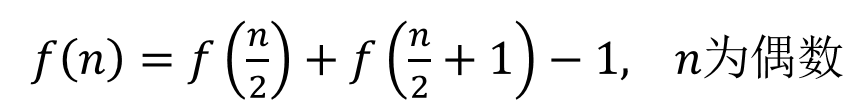
到此為止，我們雖然不會正面求f(n)，但我們得到了這樣上面這組公式。

然后簡單編個程就可以計算了，畫出男廁所坑位函數圖像長這樣。

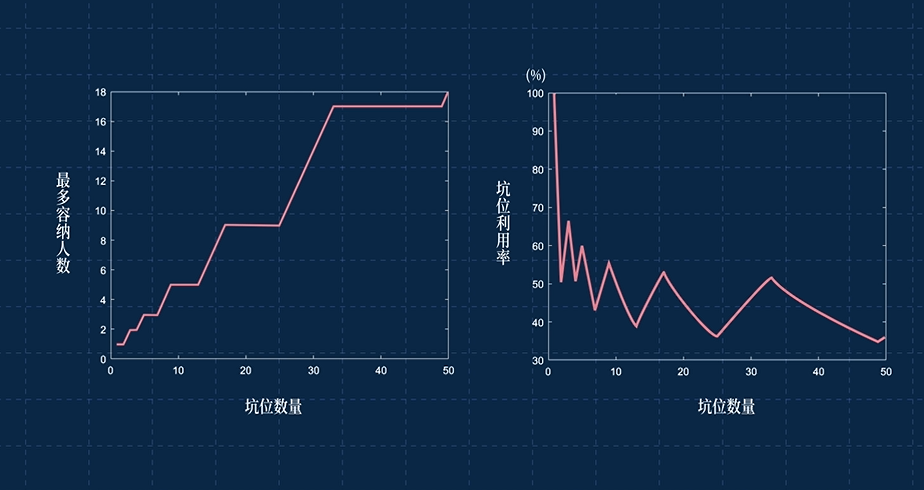
結果非常amazing啊！隨著廁所坑位數量增長，能同時容納的男生數量階梯式上升，坑位利用率振蕩式下降，最后在1/2和1/3上下反復橫跳。

廁所坑位函數有一個獨特的性質：當坑位從2^k+1增加到1.5*2^k+1時，能容納的男生數量是不變的！都等于2^(k-1)+1。

比如9、10、11、12、13個坑位的廁所，都只能容納5個人。

這告訴我們，不要盲目修太多坑位，有時候你修了也白修，男生根本就不進去。

稍加計算就會發現，一個擁有1億個坑位的宇宙級宏偉廁所至多同時容納33554433個男生，剩下66445567個坑位都會因為尷尬而被浪費掉！浪費率高達66%！

從利用率曲線來看，對于日常的廁所而言，修3、5、9、17個坑位會比較科學，利用率是最高的。修4、 7、13個坑位是最坑的。

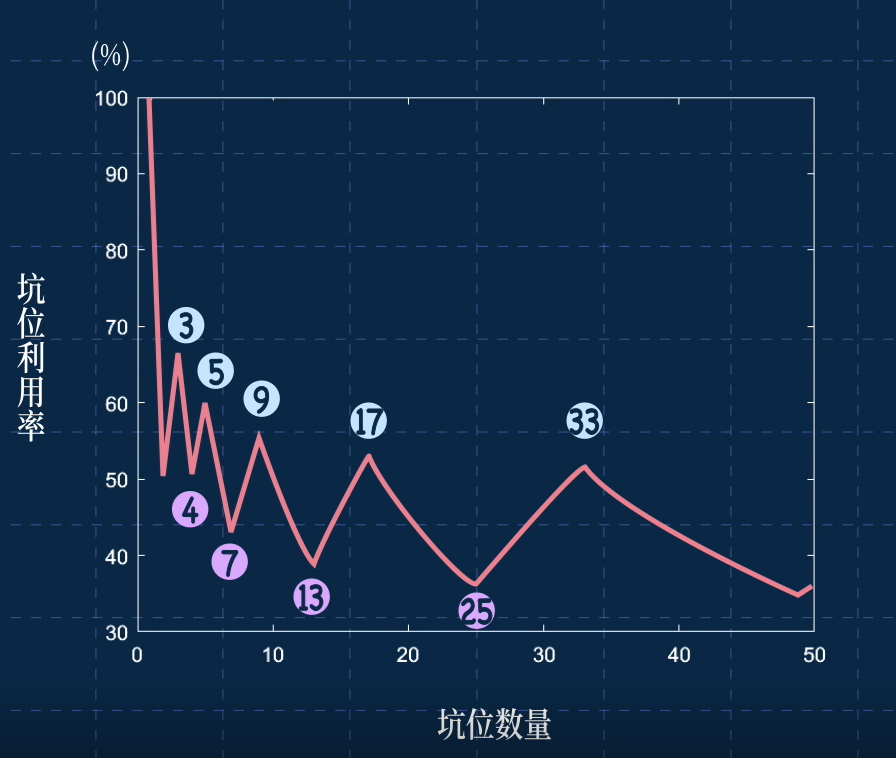
如果我的觀眾里有廁所設計師的話，希望這個結論能引起你的重視。

三、進階：男廁里的偉大思想

剛才我們解決的雖然只是廁所里一個微不足道的問題，但你仔細思考就會發現這個男廁所中，竟然蘊含著一種偉大的思想！

要求n個坑位能容納多少人，如果你排列組合分類討論，是很頭疼的。

但我們把這個問題轉化為了n/2個坑位的廁所能容納多少人的問題，然后又能轉化為n/4的問題，一直分下去，最后一定能轉化為3個坑位以內的簡單問題。這個一眼就能看出答案了。再一通合并，就能推出n個坑位的情況。

這種做法，就是我們小學二年級就學過的分而治之算法。

它的字面意思很樸素，但揭示了一種哲學思想：

把一個復雜的大問題分解為幾個相似的小問題，不斷分解，直到它變成一個個足夠小的容易解決的問題，就能治住它們，再合并解決開始的復雜問題。本質上就是個套娃思想。

舉個通俗的例子，大老板要寫論文，把論文前一半給1號小老板寫，后一半給2號小老板寫，自己合并潤色。

每個小老板又把他的部分交給兩個博士生寫，自己合并。分而治之，十分合理。結果有個博士生PS了數據，小老板沒發現，就把大老板坑了。

分而治之在數學和算法中有廣泛的應用，典型的像排序。我們大家學的第一個排序算法都是冒泡排序。依次比較相鄰元素，如果順序不對就交換。這種算法非常慢，時間復雜度是O(n2)。

但用分而治之就可以提出什么排序啊？哎對！歸并排序和快速排序。

比如你家套娃灑了一地，我們用快速排序。首先任選一個娃，將其他娃與之比較，比它大的扔它右邊，比它小的扔左邊。

現在這個娃已經找到了它最終的位置，整堆套娃被分成了左右兩個部分。在這兩部分中分別再取一個娃，比它大的放右邊，小的放左邊。

不斷套娃式重復，套娃的排序就快速完成了。快排和歸并的時間復雜度都是O(nlogn)。所以要想治住套娃，還是得用套娃。

這個視頻就直觀地演示了三種排序算法的原理和效率。

為什么分而治之會比直接剛之更加優秀呢？

這是因為，大規模問題的復雜度往往要遠遠高于小規模問題。

因此把大問題拆成容易的小問題，再遞歸地解決它們是劃算的。分治在大整數乘法、矩陣乘法、求特征值、快速傅里葉變換當中都有應用。

比如兩個8位數相乘，直接乘就要做64次個位數乘法。但我們可以分而治之，用小學二年級就學過的Karatsuba算法，把8位數分成高位和低位兩部分，一通變換猛如虎，就只要做6次加法和3次4位數乘法，相當于只有48次個位數乘法。

對電腦而言，加法比乘法好算，對人好像也是吼……把4位數乘法再次分治，乘法次數大大減少，計算效率顯著提升。

理論上講，2個1024位整數相乘，本來要做105萬次乘法，但分而治之后就只要6萬次，按現在的神童標準，口算都能算出來了。

這就是分而治之算法的威力。如今計算機的突飛猛進，既來自算力的提升，也來自算法的進步。一個巧妙的變換，就能讓解決問題的時間縮短百倍，這便是算法之美，是人類強于計算機的智慧啊！

分而治之，不光是一個算法思維，還是一種交朋友的方式。今后當你在男廁所里提著褲子等位的時候，不妨試探地拋一句

如果前面的人驚喜地回你一句

那這期視頻就讓你們突然有話題了！你們可以聊一聊這家廁所的坑位利用率是多少，玩一個套娃排序，算一個大整數乘法。

分而治之讓廁所里原本無言的尷尬化為親密的會心一笑！正道之光從此照在廁所之上。

感謝大家管看本期文章，希望給我點贊、在看，支持一下！我們下期再見！

參考文獻

1、Jon Kleinberg, éva Tardos. Algorithm Design[J]. Prentice Hall, 2005.

2、Cormen T H , Leiserson C E , Rivest R L , et al. Introduction to algorithms, third edition Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein[J]. Journal of the Operational Research Society, 2001, 42(9).

3、Cuppen J J. A divide and conquer method for the symmetric tridiagonal eigenproblem[J]. Numerische Mathematik, 1980, 36(2): 177-195.

4、 Karatsuba, Anatolii A.; Yuri P. Ofman (1962). "Умножение многозначных чисел на автоматах". Doklady Akademii Nauk SSSR. 146: 293–294.

5、Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969

6、Huang, Jianyu; Smith, Tyler; Henry, Greg; van de Geijn, Robert (2016). Strassen's Algorithm Reloaded. International Conference for High Performance Computing, Networking, Storage and Analysis (SC'16)

7、Richard Tolimieri, Chao Lu, Myoung An. Cooley-Tukey FFT Algorithms[J]. 1997