輸入原始數據(X)、平均數(M)、標準差(S)、Z分數值(Z)等4個變量中任意3個已知變量，點擊計算按鈕，可快速求出求出未知變量。

Z 分數也叫標準分數(standard score)，能夠真實的反應一個分數距離平均數的相對標準距離。如果我們把每一個分數都轉換成z分數，那么每一個z分數會以標準差為單位表示一個具體分數到平均數的距離或離差。將成正態分布的數據中的原始分數轉換為z分數，我們就可以通過查閱z分數在正態曲線下面積的表格來得知平均數與z分數之間的面積，進而得知原始分數在數據集合中的百分等級。一個數列的各z分數的平方和等于該數列數據的個數，并且z分數的標準差和方差都為1。平均數為0。

Z 分數是以標準差為尺子去度量某一原始分數偏離平均數的距離，這段距離含有幾個標準差，z分數就是幾。從而確定這一數據在全體數據中的位置。稱這一過程為標準化。

Z 分數計算公式如下：

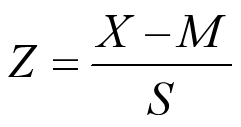
式中：X：原始數據；M：平均數；S： 標準差。

Z 分數是以標準差為單位的離均差。從Z分數的計算可以看出，由于在運算過程中保留了原始數據與平均數的差的關系(X-M),平均數的Z分數等于0，其它數值的z分數比平均數大的為正值，比平均數小的為負值。而且，任一原始數據與平均數的差的大小，決定了它的位置。所以，Z分數既能表示比其它數大多少或少多少；也可以表示該數的位置。

在統計中，Z分數是一個非常重要的指標，當原始分數的分布形態是正態分布時，把所有原始分數都轉化為Z分數，就形成了標準正態分布 。

相關計算器：