一、什么是決策樹?
決策樹(Decision Tree)是一種基本的分類和回歸的方法。
分類決策樹模型是一種描述對實例進行分類的樹形結構。決策樹由結點(node)和有向邊(directed edge)組成。結點有兩種形式:內部結點和葉節點。
一句話概括:通過信息增益,采用遞歸的方式生成樹(找出最合適的節點順序以及葉子對應的類標簽)
1.1 決策樹直觀理解
通過一個例子來理解決策樹,若我們有以下數據,要求通過以下數據,判斷某用戶是否能夠償還債務。
1.2 構建過程簡述
用決策樹分類,從根節點開始,對實例的某一特征進行測試,根據測試結果將實例分配到其子結點;這時,每一個子結點對應著該特征的一個值。如此遞歸地對實例進行測試分配,直到達到葉節點。最后將實例分到葉節點的類中。
1.3 根據構建方法構建決策樹

?
根據數據,我們主觀上覺得年收入對于是否能夠償還債務最重要,所以將年收入作為根結點。年收入大于等于97.5千元的可以償還,對于小于97.5的,再用是否擁有房產進行劃分,最后根據婚姻情況進行劃分,直到到達葉節點為止。
當構建好一個決策樹后,新來一個用戶后,可以根據決策好的模型直接進行判斷,比如新用戶為:無房產、單身、年收入55K,那么根據判斷得出該用戶無法償還債務。
二、一些概念
比特化(bits)
假設存在一組隨機變量x,各個值出現的概率關系如下:
![]()
現在有一組由x變量組成的序列:BACADDCBAC......;如果現在希望這個序列轉換為二進制來進行網絡傳輸,那么我們就得到一個這樣的序列:01001000111110010010......
在這情況下,我們可以使用兩個比特位來表示一個隨機變量。
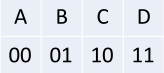
而當X變量出現的概率值不一樣的時候,對于一組序列信息來講,每個變量平均需要多少個比特位來描述呢?
![]()

計算得:
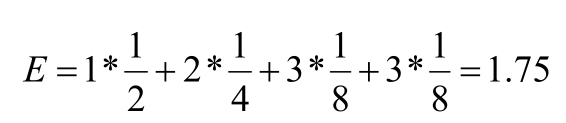
也可以使用下列方法計算
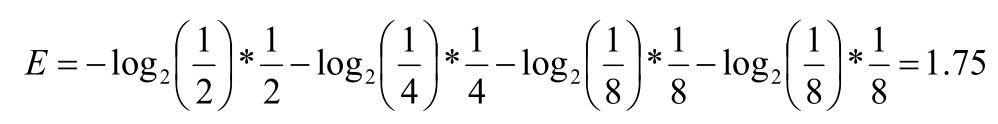
一般化的比特化(Bits)
假設現在隨機變量X具有m個值,分別為V1,v2,...vm;并且各個值出現的概率如下表所示:那么對于一組列信息來講,每個變量平均需要多少個比特位來描述呢?
![]()
可以使用這些變量的期望來表示每個變量需要多少個比特位來描述信息:
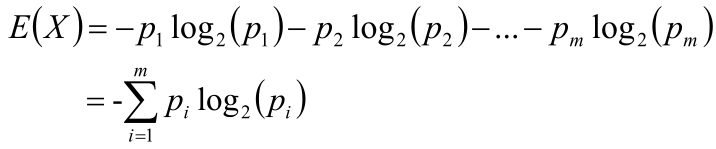
信息熵(Entropy)
公式:
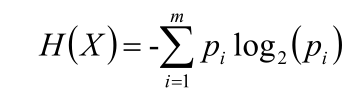
信息量:指的是一個樣本/事件所蘊含的信息,如果一個事件的概率越大,那么就可以認為該事件所蘊含的信息越少。極端情況下,比如:“太陽從東方升起”,因為是確定事件,所以不攜帶任何信息量
信息熵:1948年,香農引入信息熵;一個系統越是有序,信息熵就越低,一個系統越是混亂,信息熵就越高,所以信息熵被認為是一個系統有序程度的度量。
信息熵就是用來描述系統信息量的不確定度。
High Entropy(高信息熵):表示隨機變量X是均勻分布的,各種取值情況是等概率出現的。
Low Entropy(低信息熵):表示隨機變量X各種取值不是等概率出現。可能出現有的事件概率很大,有的事件概率很小。

條件熵H(Y|X)
給定條件 X 的情況下,隨機變量 Y 的信息熵就就叫做條件熵。

當專業(X)為數學的時候,Y的信息熵的值為:H(Y|X=數學)

給定條件X的情況下,所有不同x值情況下Y的信息熵的平均值叫做條件熵


給定條件X的情況下,所有不同x值情況下Y的信息熵的平均值叫做條件熵。另外一個公式如下所示:
![]()
事件(X,Y)發生所包含的熵,減去事件X單獨發生的熵,即為在事件X發生的前提下,Y發生“新”帶來的熵,這個也就是條件熵本身的概念,驗證如下:

三、決策樹
決策樹(Decision Tree)是在已知各種情況下發生概率的基礎上,通過構建決策樹來進行分析的一種方式,是一種直觀應用概率分析的一種圖解法;決策樹是一種預測模型,代表的是對象屬性與對象值之間的映射關系;決策樹是一種樹形結構,其中每個內部節點表示一個樹形的測試,每個分支表示一個測試輸出,每個葉子節點代表一種類別;決策樹是一種非常常用的有監督的分類算法。
決策樹的決策過程就是從根節點開始,測試待分類項中對應的特征屬性,并按照其值選擇輸出分支,知道葉子節點,將葉子節點的存放類別作為決策結果。
決策樹分為兩大類:分類樹和回歸樹,前者用于分類標簽值,后者用于預測連續值,常用算法ID3、C4.5、CART等。
決策樹構建過程
決策樹構建的重點就是決策樹的構造。決策樹的構造就是進行屬性選擇度量,確定各個特征屬性之間的拓撲結構(樹結構),構建決策樹的關鍵就是分裂屬性,構建決策樹的關鍵步驟就是分裂屬性,分裂屬性是指在某個節點按照某一特征屬性的不同劃分構建不同的分支,其目標就是讓哥哥分裂子集盡可能的“純”(讓一個分裂子類的項盡可能的屬于同一類別)
構建步驟如下:
- 將所有的特征看成一個一個的節點;
- 遍歷每個特征的每一種分割方式,找到最好的分割點;將數據劃分為不同的子節點,eg:
、
....
;計算劃分之后所有子節點的'純度'信息;
- 對第二步產生的分割,選擇出最優的特征以及最優的劃分方式;得出最終的子節點:
、
....
- 對子節點
、
....
分別繼續執行2-3步,直到每個最終的子節點都足夠'純'。
決策樹特征屬性類型
根據特征屬性的類型不同,在構建決策樹的時候,采用不同的方式,具體如下:
- 屬性是離散值,而且不要求生成的是二叉決策樹,此時一個屬性就是一個分支
- 屬性是離散值,而且要求生成的是二叉決策樹,此時使用屬性劃分的子集進行測試,按照“屬于此子集”和“不屬于此子集”分成兩個分支
- 屬性是連續值,可以確定一個值作為分裂點split_point,按照 >split_point 和 <=split_point 生成兩個分支
決策樹分割屬性選擇
決策樹算法是一種“貪心”算法策略,只考慮在當前數據特征情況下的最好分割方式,不能進行回溯操作。
對于整體的數據集而言,按照所有的特征屬性進行劃分操作,對所有劃分操作的結果集的“純度”進行比較,選擇“純度”越高的特征屬性作為當前需要分割的數據集進行分割操作,持續迭代,直到得到最終結果。決策樹是通過“純度”來選擇分割特征屬性點的。
?決策樹量化純度
決策樹的構建是基于樣本概率和純度進行構建操作的,那么進行判斷數據集是否“純”可以通過三個公式進行判斷,分別是Gini系數、熵(Entropy)、錯誤率,一般情況使用熵公式。
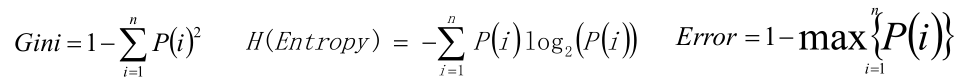
當計算出各個特征屬性的量化純度值后使用信息增益度來選擇出當前數據集的分割特征屬性;如果信息增益度的值越大,表示在該特征屬性上會損失的純度越大 ,那么該屬性就越應該在決策樹的上層,計算公式為:
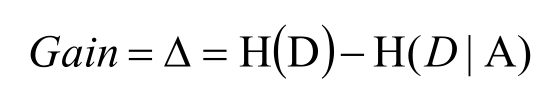
Gain為A為特征對訓練數據集D的信息增益,它為集合D的經驗熵H(D)與特征A給定條件下D的經驗條件熵H(D|A)之差。
決策樹的停止條件
一般情況有兩種停止條件:
- 當每個子節點只有一種類型的時候停止構建。
- 當前節點中記錄數小于某個閾值,同時迭代次數達到給定值時,停止構建過程,此時使用max(p(i))作為節點的對應類型。
方式一可能會使樹的節點過多,導致過擬合(Overfiting)等問題;比較常用的方式是使用方式二作為停止條件。
決策樹算法效果的評估
決策樹的效果評估和一般的分類算法一樣,采用混淆矩陣來進行計算準確率、召回率、精確率等指標。
也可以采用葉子節點的純度值總和來評估算法的效果,值越小,效果越好。

決策樹的損失函數(該值越小,算法效果越好)。
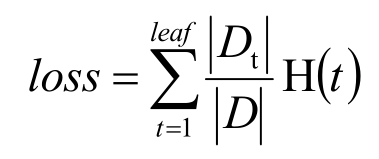
四、決策樹直觀理解結果計算

?
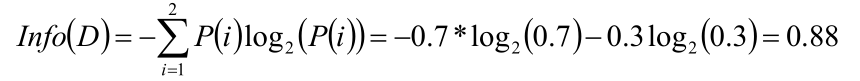
2、對數據特征進行分割
該數據的特征共有三個,分別計算每個特征的條件熵
按照是否擁有房產分別計算,然后算出條件熵
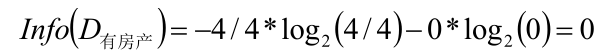
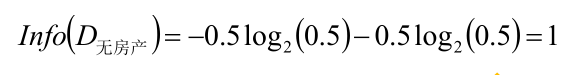
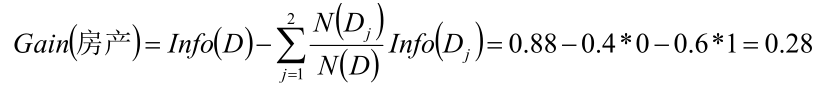
同理可以計算Gain(D,婚姻)=0.205

只保留80和97.5。?如果選擇67.5,它將60和75分開了,但是60和75的Y都是否,標簽相同,最好還是分到一個類中
Gain(D,年收入=97.5)=0.395
Gain(D,年收入=80)=0.116
按照Gain越小,分割后的純度越高,因此第一個分割的特征屬性為年收入,并按照97.5進行劃分。

左子樹的結果集夠純,因此不需要繼續劃分。接下來,對右子樹年收入<97.5的數據,繼續選擇特征進行劃分,且不再考慮收入這個特征,注意需要重新計算Gain(D,婚姻),Gain(D,房產),重復上述步驟,至到滿足結束條件
五、算法
ID3算法
ID3算法是決策樹的一個經典的構造算法,內部使用信息熵以及信息增益來進行構建;每次迭代選擇信息增益最大的特征屬性作為分割屬性。
信息熵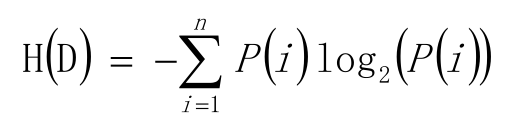
信息增益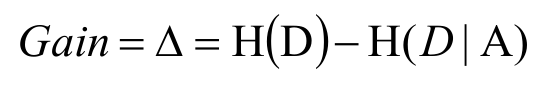
優點:
決策樹構建速度快;實現簡單;
缺點:
- 計算依賴于特征數目較多的特征,而屬性值最多的屬性并不一定最優
- ID3算法不是遞增算法
- ID3算法是單變量決策樹,對于特征屬性之間的關系不會考慮
- 抗噪性差
- 只適合小規模數據集,需要將數據放到內存中
C4.5算法
在ID3算法的基礎上,進行算法優化提出的一種算法;使用信息增益率來取代ID3算法中的信息增益,在樹的構造過程中會進行剪枝操作進行優化;能夠自動完成對連續屬性的離散化處理;C4.5算法在選中分割屬性的時候選擇信息增益率最大的屬性,涉及到的公式為:

優點
- 產生的規則易于理解
- 準確率較高
- 實現簡單
缺點:
- 對數據集需要進行多次順序掃描和排序,所以效率較低
- 只適合小規模數據集,需要將數據放到內存中。
CART算法
使用基尼系數作為數據純度的量化指標來構建的決策樹算法就叫做CART(Classification And Regression Tree,分類回歸樹)算法。CART算法使用GINI增益作為分割屬性選擇的標準,選擇GINI增益最大的作為當前數據集的分割屬性;可用于分類和回歸兩類問題。強調:CART構建是二叉樹。
基尼系數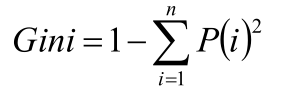
基尼增益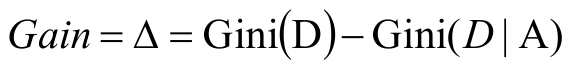
ID3、C4.5、CART分類樹算法總結
- ID3和C4.5算法均只適合在小規模數據集上使用
- ID3和C4.5算法都是單變量決策樹
- 當屬性值取值比較多的時候,最好考慮C4.5算法,ID3得出的效果會比較差
- 決策樹分類一般情況只適合小數據量的情況(數據可以放內存)
- CART算法是三種算法中最常用的一種決策樹構建算法。
- 三種算法的區別僅僅只是對于當前樹的評價標準不同而已,ID3使用信息增益、
- C4.5使用信息增益率、CART使用基尼系數。
- CART算法構建的一定是二叉樹,ID3和C4.5構建的不一定是二叉樹。
| 算法 | 支持模型 | 樹結構 | 特征選擇 | 連續值處理 | 缺失值處理 | 剪枝特征屬性多次使用 |
|---|---|---|---|---|---|---|
| ID3 | 分類 | 多叉樹 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分類 | 多叉樹 | 信息增益率 | 支持 | 支持 | 支持 |
| CART | 分類、回歸 | 二叉樹 | 基尼系數、均方差 | 支持 | 支持 | 支持 |
六、分類樹和回歸樹
分類樹采用信息增益、信息增益率、基尼系數來評價樹的效果,都是基于概率值進行判斷的;而分類樹的葉子節點的預測值一般為葉子節點中概率最大的類別作為當前葉子的預測值。
回歸樹中,葉子節點的預測值一般為葉子節點中所有值的均值來作為當前葉子節點的預測值。所以在回歸樹中一般采用MSE作為樹的評價指標,即均方差。一般情況,使用CART算法構建回歸樹。

七、決策樹的優化策略
剪枝優化:決策樹過渡擬合一般情況是由于節點太多導致的,剪枝優化對決策樹的正確率影響是比較大的,也是最常用的一種優化方式。
Random Forest:利用訓練數據隨機產生多個決策樹,形成一個森林。然后使用這個森林對數據進行預測,選取最多結果作為預測結果。
剪枝優化
決策樹的剪枝是決策樹算法中最基本、最有用的一種優化方案,主要分為兩大類:
前置剪枝:在構建決策樹的過程中,提前停止。結果是決策樹一般比較小,實踐證明這種策略無法得到比較好的結果。
后置剪枝:在決策樹構建好后,然后再開始裁剪,一般使用兩種方式:1、用單一葉子節點代替整個子樹,葉節點的分類采用子樹中最主要的分類;2、將一個子樹完全替代另外一棵子樹;后置剪枝的主要問題是計算效率問題,存在一定的浪費情況。
后置剪枝過程:
對于給定的決策樹T0
- 計算所有內部非葉子節點的剪枝系數;
- 查找最小剪枝系數的節點,將其子節點進行刪除操作,進行剪枝得到決策樹Tk;如果存在多個最小剪枝系數節點,選擇包含數據項最多的節點進行剪枝操作;
- 重復上述操作,直到產生的剪枝決策樹Tk只有1個節點;
- 得到決策樹T0 T1 T2....Tk;
- 使用驗證樣本集選擇最優子樹Ta(使用原始損失函數考慮)。
使用驗證集選擇最優子樹的標準,可以使用原始損失函數來考慮:
八、決策樹剪枝損失函數及剪枝系數
原始損失函數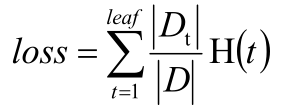
葉節點越多,決策樹越復雜,損失越大;修正添加剪枝系數,修改后的損失函數為
![]()
考慮根節點為r的子樹,剪枝前后的損失函數分別為loss(R)和loss(r),當這兩者相等的時候,可以求得剪枝系數
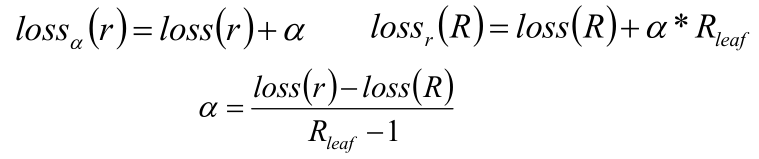
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
)





)






)
)




