距離知識
點到直線/平面的距離公式:
1、假定點p(x0,y0),平面方程為f(x,y)=Ax+By+C,那么點p到平面f(x)的距離為:
2、從三維空間擴展到多維空間中,如果存在一個超平面f(X)=θX+b; 那么某一個點X0到這個超平面的距離為:
參考文獻:https://wenku.baidu.com/view/d26d2ba39e31433239689374.html
感知器模型
感知器算法是最古老的分類算法之一,原理比較簡單,不過模型的分類泛化能力比較弱,不過感知器模型是SVM、神經網絡、深度學習等算法的基礎。
感知器的思想很簡單:比如有很多的學員生,分為男學生和女學生,感知器模型就是試圖找到一條直線,能夠把所有的男學生和女學生分隔開,如果是高維空間中,感知器模型尋找的就是一個超平面,能夠把所有的二元類別分割開。感知器模型的前提是:數據是線性可分的。
對于m個樣本,每個樣本n維特征以及一個二元類別輸出y,如下:
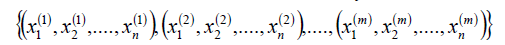
目標是找到一個超平面,即:
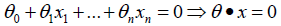
讓一個類別的樣本滿足:?;另外一個類別的滿足:
。感知器模型為:
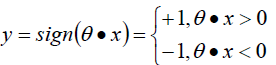
正確分類:?,錯誤分類:
?;所以我們可以定義我們的損害函數為:期望使分類錯誤的所有樣本(m條樣本)到超平面的距離之和最小。
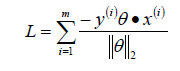
因為此時分子和分母中都包含了θ值,當分子擴大N倍的時候,分母也會隨之擴大,也就是說分子和分母之間存在倍數關系,所以可以固定分子或者分母為1,然后求另一個即分子或者分母的倒數的最小化作為損失函數,簡化后的損失函數為(分母為1)
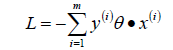 :
:
直接使用梯度下降法就可以對損失函數求解,不過由于這里的m是分類錯誤的樣本點集合,不是固定的,所以我們不能使用批量梯度下降法(BGD)求解,只能使用隨機梯度下降(SGD)或者小批量梯度下降(MBGD);一般在感知器模型中使用SGD來求解。
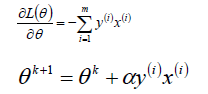
SVM
支持向量機(Support Vecor Machine, SVM)本身是一個二元分類算法,是對感知器算法模型的一種擴展,現在的SVM算法支持線性分類和非線性分類的分類應用,并且也能夠直接將SVM應用于回歸應用中,同時通過OvR或者OvO的方式我們也可以將SVM應用在多元分類領域中。在不考慮集成學習算法,不考慮特定的數據集的時候,在分類算法中SVM可以說是特別優秀的。
線性可分SVM
在感知器模型中,算法是在數據中找出一個劃分超平面,讓盡可能多的數據分布在這個平面的兩側,從而達到分類的效果,但是在實際數據中這個符合我們要求的超平面是可能存在多個的。

在感知器模型中,可以找到多個可以分類的超平面將數據分開,并且優化時希望所有的點都離超平面盡可能的遠,但是實際上離超平面足夠遠的點基本上都是被正確分類的,所以這個是沒有意義的;反而比較關心那些離超平面很近的點,這些點比較容易分錯。所以說我們只要讓離超平面比較近的點盡可能的遠離這個超平面。
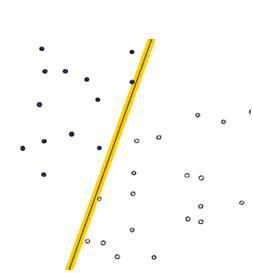
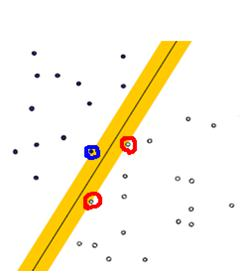
- 線性可分(Linearly Separable):在數據集中,如果可以找出一個超平面,將兩組數據分開,那么這個數據集叫做線性可分數據。
- 線性不可分(Linear Inseparable):在數據集中,沒法找出一個超平面,能夠將兩組數據分開,那么這個數據集就叫做線性不可分數據。
- 分割超平面(Separating Hyperplane):將數據集分割開來的直線/平面叫做分割超平面。
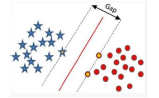
- 間隔(Margin):數據點到分割超平面的距離稱為間隔。
- 支持向量(Support Vector):離分割超平面最近的那些點叫做支持向量。
支持向量到超平面的距離為:

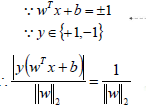
備注:在SVM中支持向量到超平面的函數距離一般設置為1。
SVM模型是讓所有的分類點在各自類別的支持向量的兩邊,同時要求支持向量盡可能的原理這個超平面,用數學公式表示如下:
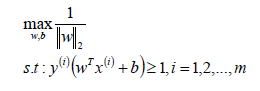
將上式子優化為SVM的損失函數為:
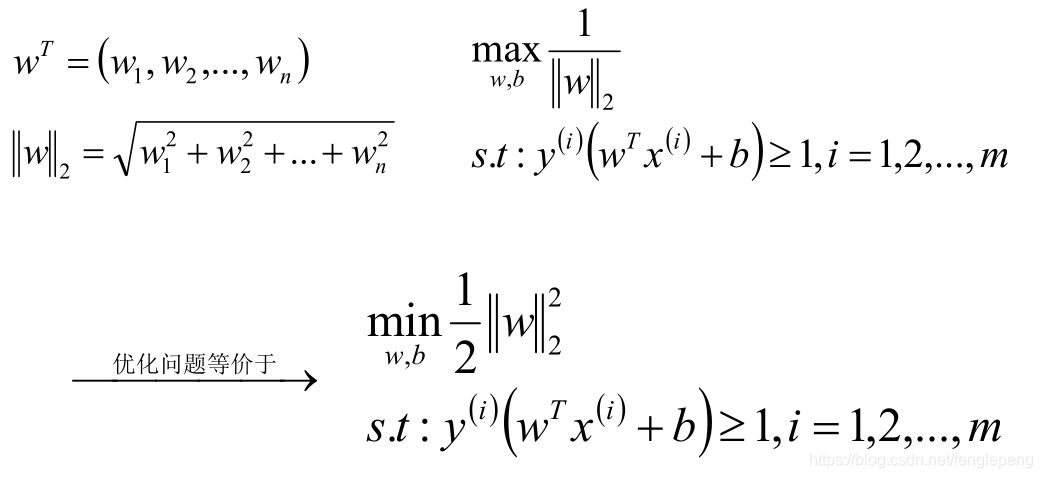
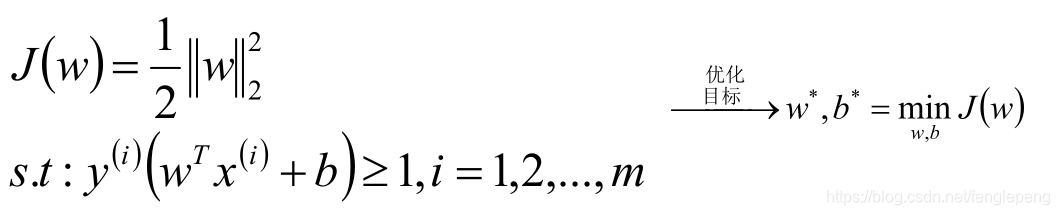
將此時的目標函數和約束條件使用KKT條件轉換為拉格朗日函數,從而轉換為無約束的優化函數。
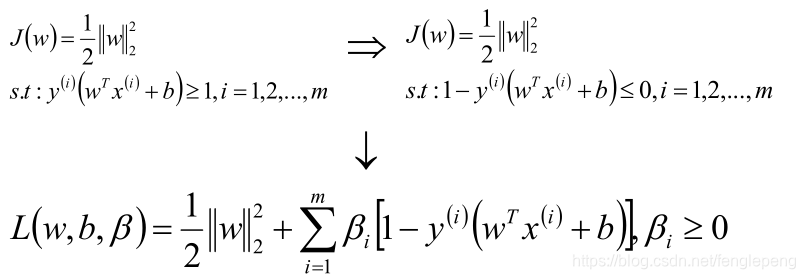
引入拉格朗日乘子后,優化目標變成:
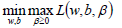
根據拉格朗日對偶化特性,將該優化目標轉換為等價的對偶問題來求解,從而優化目標變成:
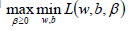
所以對于該優化函數而言,可以先求優化函數對于w和b的極小值,然后再求解對于拉格朗日乘子β的極大值。
首先求讓函數L極小化的時候w和b的取值,這個極值可以直接通過對函數L分別求w和b的偏導數得到:
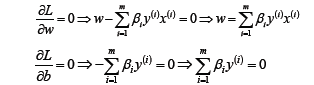
將求解出來的w和b帶入優化函數L中,定義優化之后的函數如下:
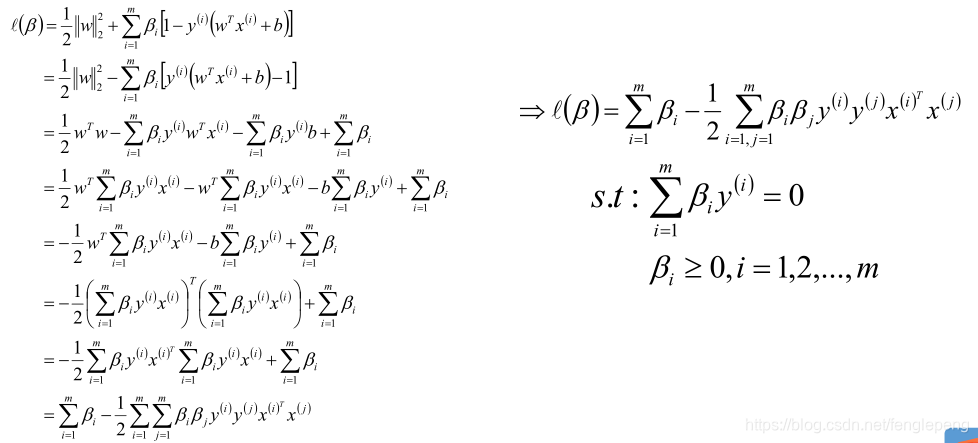
通過對w、b極小化后,我們最終得到的優化函數只和β有關,所以此時我們可以直接極大化我們的優化函數,得到β的值,從而可以最終得到w和b的值。

假設存在最優解β*; 根據w、b和β的關系,可以分別計算出對應的w值和b值(一般使用所有支持向量的計算均值來作為實際的b值);
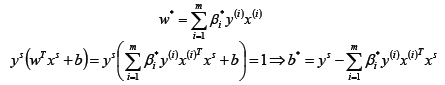
這里的(xs,ys)即支持向量,根據KKT條件中的對偶互補條件(松弛條件約束),支持向量必須滿足一下公式:
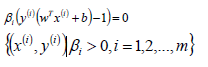
2.1.1 算法流程
輸入線性可分的m個樣本數據{(x1,y1),(x2,y2),…,(xm,ym)},其中x為n維的特征向量,y為二元輸出,取值為+1或者-1;SVM模型輸出為參數w、b以及分類決策函數。
構造約束優化問題;
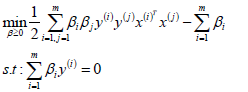
使用SMO算法求出上式優化中對應的最優解β*;
找出所有的支持向量集合S;
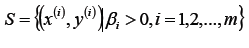
更新參數w*、b*的值;
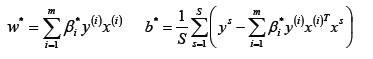
構建最終的分類器。
算法總結
- 要求數據必須是線性可分的;
- 純線性可分的SVM模型對于異常數據的預測可能會不太準;
- 對于線性可分的數據,SVM分類器的效果非常不錯。
2.2 SVM的軟間隔模型
線性可分SVM中要求數據必須是線性可分的,才可以找到分類的超平面,但是有的時候線性數據集中存在少量的異常點,由于這些異常點導致了數據集不能夠線性劃分;直白來講就是:正常數據本身是線性可分的,但是由于存在異常點數據,導致數據集不能夠線性可分;
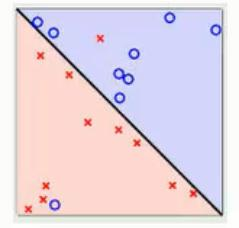
如果線性數據中存在異常點導致沒法直接使用SVM線性分割模型的時候,可以通過引入軟間隔的概念來解決這個問題;
硬間隔:可以認為線性劃分SVM中的距離度量就是硬間隔,在線性劃分SVM中,要求函數距離一定是大于1的,最大化硬間隔條件為: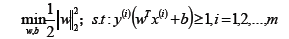
軟間隔:SVM對于訓練集中的每個樣本都引入一個松弛因子(ξ),使得函數距離加上松弛因子后的值是大于等于1;這表示相對于硬間隔,對樣本到超平面距離的要求放松了。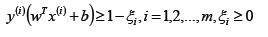
松弛因子(ξ)越大,表示樣本點離超平面越近,如果松弛因子大于1,那么表示允許該樣本點分錯,所以說加入松弛因子是有成本的,過大的松弛因子可能會導致模型分類錯誤,所以最終的目標函數就轉換成為:
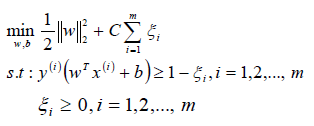
備注:函數中的C>0是懲罰參數,是一個超參數,類似L1/L2 norm的參數;C越大表示對誤分類的懲罰越大,C越小表示對誤分類的懲罰越小;C值的給定需要調參。
同線性可分SVM,構造軟間隔最大化的約束問題對應的拉格朗日函數如下:
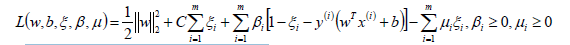
從而將我們的優化目標函數轉換為:
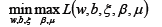
優化目標同樣滿足KKT條件,所以使用拉格朗日對偶將優化問題轉換為等價的對偶問題:
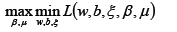
先求優化函數對于w、b、ξ的極小值,這個可以通過分別對優化函數L求w、b、ξ的偏導數得,從而可以得到w、b、ξ關于β和μ之間的關系。
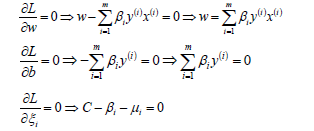
將w、b、ξ的值帶入L函數中,就可以消去優化函數中的w、b、ξ,定義優化之后的函數如下:
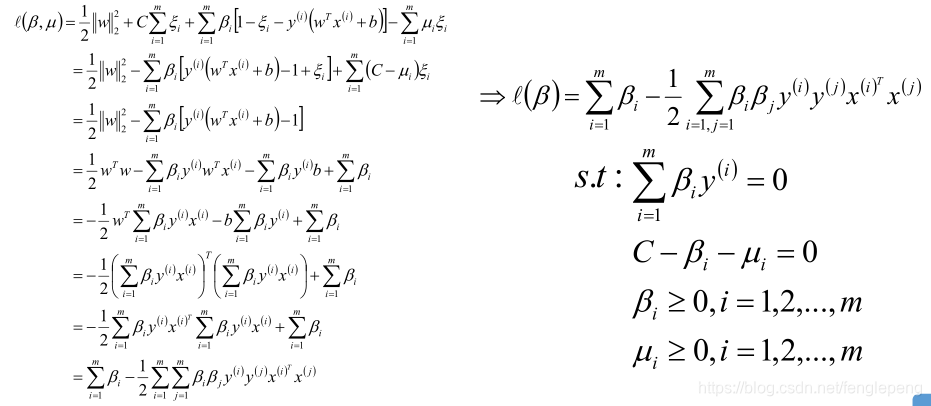
最終優化后的目標函數/損失函數和線性可分SVM模型基本一樣,除了約束條件不同而已, 也就是說也可以使用SMO算法來求解。
在硬間隔最大化的時候,支持向量比較簡單,就是離超平面的函數距離為1的樣本點就是支持向量。
在軟間隔中,根據KKT條件中的對偶互補條件: β(y(wx+b)-1+ξ)=0,從而有:當0<β i ≤C的時候,并且ξ i =0的樣本點均是支持向量(即所有的0<β i <C)。即滿足|wx+b|=1的所有樣本均是支持向量。
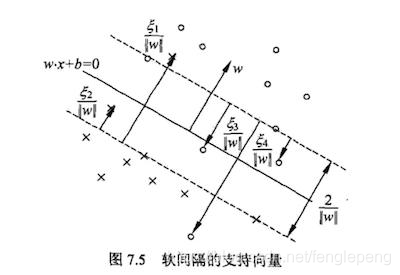
備注:軟間隔和硬間隔中的支持向量的規則是一樣的;
算法流程
輸入線性可分的m個樣本數據{(x1,y1),(x2,y2),…,(xm,ym)},其中x為n維的特征向量,y為二元輸出,取值為+1或者-1;SVM模型輸出為參數w、b以及分類決策函數。
選擇一個懲罰系數C>0,構造約束優化問題;
使用SMO算法求出上式優化中對應的最優解β*;
找出所有的支持向量集合S;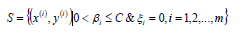
更新參數w*、b*的值;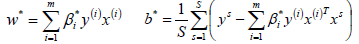
構建最終的分類器。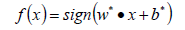
算法總結
- 可以解決線性數據中攜帶異常點的分類模型構建的問題;
- 通過引入懲罰項系數(松弛因子),可以增加模型的泛化能力,即魯棒性;
- 如果給定的懲罰項系數越小,表示在模型構建的時候,就允許存在越多的分類錯誤的樣本, 也就表示此時模型的準確率會比較低;如果懲罰項系數越大,表示在模型構建的時候,就越不允許存在分類錯誤的樣本,也就表示此時模型的準確率會比較高。
非線性可分SVM
不管是線性可分SVM還是加入懲罰系數后的軟間隔線性可分SVM其實都要求數 據本身是線性可分的,對于完全不可以線性可分的數據,這兩種算法模型就沒法 解決這個問題了。
在線性回歸中,我們可以通過多項式擴展將低維度的數據擴展成為高維度的數據,從而可以使用線性回歸模型來解決問題。 也就是說對于二維空間中不是線性可分的數據,將其映射到高維空間中后,變成了線性可分的數據。
結合多項式回歸在處理非線性可分數據時候的作用,在SVM的線性不可分的數據上,如果將數據映射到高維空間中,那么數據就會變成線性可分的,從而就可以使用線性可分SVM模型或者軟間隔線性可分SVM模型。
也就是說,對于線性不可分SVM模型來講,重點在于低維特征數據到高維特征數據之間的映射。
定義一個從低維特征空間到高維特征空間的映射函數Ф,非線性可分SVM的優化目標函數:
可以看到的是,只需要將原來的低維空間中的兩個向量的點積轉換為高維空間中兩個向量的點積即可。
這樣一來問題就解決了嗎?似乎是的:拿到非線性數據,就找一個映射,然后一股腦把原來的數據映射到新空間中,再做線性 SVM 即可。不過事實上沒有這么簡單!其實剛才的方法稍想一下就會發現有問題:在最初的例子里做了一個二階多項式的轉換,對一個二維空間做映射,選擇的新空間是原始空間的所有一階和二階的組合,得到了5個維度;如果原始空間是三維,那么我們會得到9維的新空間;如果原始空間是n維,那么我們會得到一個n(n+3)/2維的新空間;這個數目是呈爆炸性增長的,這給計算帶來了非常大的困難,而且如果遇到無窮維的情況, 就根本無從計算。
核函數
假設函數Ф是一個從低維特征空間到高維特征空間的一個映射,那么如果存在函數K(x,z), 對于任意的低維特征向量x和z,都有:
稱函數K(x,z)為核函數(kernal function);
核函數:在低維空間上的計算量等價于特征做維度擴展后的點乘的結果。
核函數在解決線性不可分問題的時候,采取的方式是:使用低維特征空間上的計算來避免在高維特征空間中向量內積的恐怖計算量;也就是說此時SVM模型可以應用在高維特征空間中數據可線性分割的優點,同時又避免了引入這個高維特征空間恐怖的內積計算量。
即:用低維空間中少的內積的計算量來讓模型具有高維空間中的線性可分的優點。
不妨還是從最開始的簡單例子出發,設兩個向量?
而即是到前面說的五維空間的映射,因此映射過后的內積為:
而同時我們可以發現有一下公式:
可以發現兩者之間非常相似,所以我們只要乘上一個相關的系數,就可以讓這兩個式子的值相等,這樣不就將五維空間的一個內積轉換為兩維空間的內積的運算。
現有有兩個兩維的向量,進行二階多項式擴展,然后進行內積計算,這個時候映射高維后計算的計算量為:11次乘法+4次加法;采用近似計算的計算量為:3次乘法+2次加法;采用加系數后的近似計算的計算量為:4次乘法+2次加法;
線性核函數(Linear Kernel):
?
多項式核函數(Polynomial Kernel):其中γ、r、d屬于超參,需要調參定義;
高斯核函數(Gaussian Kernel):其中γ屬于超參,要求大于0,需要調參定義;
Sigmoid核函數(Sigmoid Kernel):其中γ、r屬于超參,需要調參定義;
核函數總結
核函數可以自定義;核函數必須是正定核函數,即Gram矩陣是半正定矩陣;
核函數的價值在于它雖然也是將特征進行從低維到高維的轉換,但核函數它事先在低維上進行計算,而將實質上的分類效果表現在了高維上,也就如上文所說的避免了直接在高維空間中的復雜計算;
通過核函數,可以將非線性可分的數據轉換為線性可分數據;
核函數的優先選擇
- 分類:線性核函數、多項式核函數(poly)、高斯核函數(rbf)
- 回歸:高斯核函數
高斯核公式證明(擴展)
令z=x;那么進行多維變換后,應該是同一個向量,從而可以得到以下公式:
?
SMO
序列最小優化算法(Sequential minimal optimization, SMO)是一種用于解決 SVM訓練過程中所產生的優化問題的算法。 于1998年由John Platt發明
假定存在一個β* =(β1?,β2?,...,βm)是我們最終的最優解,那么根據KKT條件我們可以 計算出w和b的最優解,如下:
進而我們可以得到最終的分離超平面為:
拉格朗日乘子法和KKT的對偶互補條件為:
β、μ和C之間的關系為:
根據這個對偶互補條件,我們有如下關系式:
也就是說我們找出的最優的分割超平面必須滿足下列的目標條件(g(x)):
拉格朗日對偶化要求的兩個限制的初始條件為:
從而可以得到解決問題的思路如下:
- 首先,初始化后一個β值,讓它滿足對偶問題的兩個初始限制條件;
- 然后不斷優化這個β值,使得由它確定的分割超平面滿足g(x)目標條件;而且在優化過程中,始終保證β值滿足初始限制條件。
- 備注:這個求解過程中,和傳統的思路不太一樣,不是對目標函數求最小值,而是 讓g(x)目標條件盡可能的滿足。
在這樣一個過程中,到底如何優化這個β值呢???整理可以發現β值的優化必 須遵循以下兩個基本原則:
- 每次優化的時候,必須同時優化β的兩個分量;因為如果只優化一個分量的話,新的β值就沒法滿足初始限制條件中的等式約束條件了。
- 每次優化的兩個分量應該是違反g(x)目標條件比較多的。也就是說,本來應當是大于等于1的,越是小于1違反g(x)目標條件就越多。
或者換一種思路來理解,因為目標函數中存在m個變量,直接優化比較難,利用啟發式的方法/EM算法的思想,每次優化的時候,只優化兩個變量,將其它的變量看成常數項,這樣SMO算法就將一個復雜的優化算法轉換為一個比較簡單的兩變量優化問題了。
認為β1、β2是變量,其它β值是常量,從而將目標函數轉換如下(C是常數項):
由于β1y1?+?β2y2?= k? ?,并且y1=1或者-1,也就是我們使用β2來表示β1的值:
將上式帶入目標優化函數,就可以消去β1,從而只留下僅僅包含β2的式子。
考慮β1和β2的取值限定范圍,假定新求出來的β值是滿足我們的邊界限制的,即 如下所示:
?
當y1=y2的時候,β1+β2=k; 由于β的限制條件,我們可以得到:
當y1≠y2的時候,β1?- β2=k; 由于β的限制條件,我們可以得到:
結合β的取值限制范圍以及函數W的β最優解,我們可以得帶迭代過程中的最優 解為:
然后根據β1和β2的關系,從而可以得到迭代后的β1的值:
求解β的過程中,相關公式如下:
可以發現SMO算法中,是選擇兩個合適的β變量做迭代,其它變量作為常量來進 行優化的一個過程,那么這兩個變量到底怎么選擇呢???
- 每次優化的時候,必須同時優化β的兩個分量;因為如果只優化一個分量的話,新的β值就沒法滿足初始限制條件中的等式約束條件了。
- 每次優化的兩個分量應該是違反g(x)目標條件比較多的。也就是說,本來應當是大于等于1的,越是小于1違反g(x)目標條件就越多。
第一個β變量的選擇
SMO算法在選擇第一個β變量的時候,需要選擇在訓練集上違反KKT條件最嚴重的樣本點。一般情況下,先選擇0<β<C的樣本點(即支持向量),只有當所有的支持向量都滿足KKT條件的時候,才會選擇其它樣本點。因為此時違反KKT條件越嚴重,在經過一次優化后,會讓變量β盡可能的發生變化,從而可以以更少的迭代次數讓模型達到g(x)目標條件。
?
在選擇第一個變量β1后,在選擇第二個變量β2的時候,希望能夠按照優化后的β1和β2有盡可能多的改變來選擇,也就是說讓|E1-E2?|足夠的大,當E1為正的時候, 選擇最小的Ei作為E2;當E1為負的時候,選擇最大的Ei作為E2。
備注:如果選擇的第二個變量不能夠讓目標函數有足夠的下降,那么可以通過遍歷所有樣本點來作為β2,直到目標函數有足夠的下降,如果都沒有足夠的下降的話,那么直接跳出循環,重新選擇β1;
在每次完成兩個β變量的優化更新之后,需要重新計算閾值b和差值Ei。當0<β1new<C時,有:
化簡可得:
? ?
計算閾值b和差值Ei
同樣的當β2的取值為: 0<β2<C的時候,我們也可以得到:
最終計算出來的b為:
當更新計算閾值b后,就可以得到差值Ei為:
SMO算法流程總結
輸入線性可分的m個樣本數據{(x1?,y1,(x2?,y2),...,(xm?,ym)},其中x為n維的特征向量, y為二元輸出,取值為+1或者-1;精度為e。
- 取初值β0=0,k=0;
- 選擇需要進行更新的兩個變量: β1k和β2k?,計算出來新的β2new,unt;
- 按照下列式子求出具體的β2k+1;
- 按照?β1k和β2k的關系,求出β1k+1的值:
- 按照公式計算bk+1和Ei的值;
- 檢查函數y(i)*Ei的絕對值是否在精度范圍內,并且求解出來的β解滿足KKT相關約束條件,那么此時結束循環,返回此時的β解即可,否則繼續迭代計算β2new,unt的值。
SVR
SVM和決策樹一樣,可以將模型直接應用到回歸問題中;在SVM的分類模型 (SVC)中,目標函數和限制條件如下:
在SVR中,目的是為了盡量擬合一個線性模型y=wx+b;從而我們可以定義常量eps>0,對于任意一點(x,y),如果|y-wx-b|≤eps,那么認為沒有損失,從而我們可以得到目標函數和限制條件如下:
?
加入松弛因子ξ>0,從而我們的目標函數和限制條件變成:
構造拉格朗日函數:
拉格朗日函數對偶化
首先來求優化函數對于w、b、ξ的極小值,通過求導可得:
將w、b、ξ的值帶入函數L中,就可以將L轉換為只包含β的函數,從而我們可以得到最終的優化目標函數為(備注:對于β的求解照樣可以使用SMO算法來求解):
分類算法模型的選擇方式
比較邏輯回歸、KNN、決策樹、隨機森林、GBDT、Adaboost、SVM等分類算 法的效果,數據集使用sklearn自帶的模擬數據進行測試。
我們首先看數據量,如果數據量多,那使用簡單算法(eg: KNN、Logtistic);如果數據量少,首先使用簡單執行速度快的算法(Logitsic回歸、LinearSVC、決策樹),然后如果基礎算法效果不好,那么考慮集成算法或者SVC(rbf)。
?
?









--受傷的總是我)







!!!...)
)
