目錄
貝葉斯定理
樸素貝葉斯算法
高斯樸素貝葉斯
伯努利樸素貝葉斯
多項式樸素貝葉斯
貝葉斯網絡
最簡單的貝葉斯網絡
全連接貝葉斯網絡
一般化的貝葉斯網絡
引子
參賽者會看見三扇關閉了的門,其中一扇的后面有一輛汽車,選中后面有車的那扇門可贏得該汽車,另外兩扇門后面則各藏有一只山羊。當參賽者選定了一扇門,但未去開啟它的時候,節目主持人開啟剩下兩扇門的其中一扇,露出其中一只山羊。主持人其后會問參賽者要不要換另一扇仍然關上的門。問題是:換另一扇門會否增加參賽者贏得汽車的機率?
貝葉斯定理
先驗概率P(A):在不考慮其他的情況下,A事件發生的概率。
條件概率P(B|A):A事件發生的情況下,B事件發生的概率。
后驗概率P(A|B):在B事件發生之后,對A事件發生的概率的重新評估。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
全概率:如果A和A’ 構成樣本空間的一個劃分,那么事件B的概率為A和A’ 的概率分別乘以B對這兩個事件的概率之和。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
基于條件概率的貝葉斯定律數學公式:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
樸素貝葉斯算法
樸素貝葉斯(Naive Bayes, NB)是基于“特征之間是獨立的”這一樸素假設,應用貝葉斯定理的監督學習算法。對應給定的樣本X的特征向量,該樣本X的類別y的概率可以由貝葉斯公式得到:
? ? ? ? ? ? ? ? ? ? ? ? ??
算法推導
特征屬性之間是獨立的,所以
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
公式優化得到:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
在給定樣本的條件下,是常數,可以省略,得到:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
從而得到
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
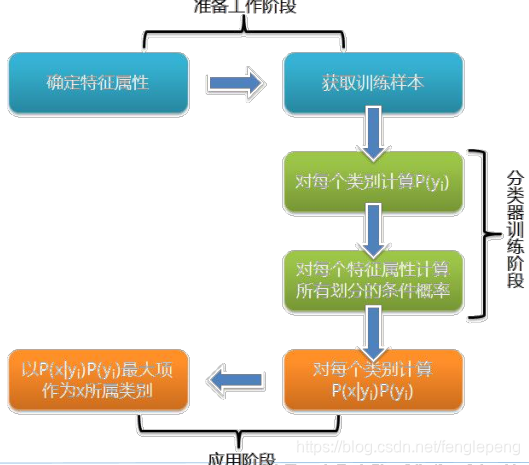
樸素貝葉斯算法流程:
- 設?
?為待分類項,其中a為x的一個特征屬性
- 類別集合為
- 分別用貝葉斯公式計算
的值,、
- 如果
,那么認為x為?
?類型
高斯樸素貝葉斯
Gaussian Naive Bayes是指當特征屬性為連續值時,而且分布服從高斯分布,那么在計算P(x|y)的時候可以直接使用高斯分布的概率公式:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
因此只需要計算出各個類別中此特征項劃分的各個均值和標準差。
伯努利樸素貝葉斯
Bernoulli Naive Bayes是指當特征屬性為連續值時,而且分布服從伯努利分布,那么在計算P(x|y)的時候可以直接使用伯努利分布的概率公式:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
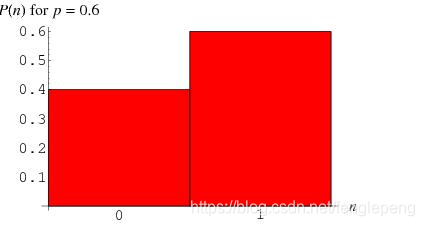
伯努利分布是一種離散分布,只有兩種可能的結果。1表示成功,出現的概率為p。0表示失敗,出現的概率為q=1-p。其中均值為E(x)=p,方差為Var(X)=p(1-p)。
多項式樸素貝葉斯
Multinomial Naive Bayes是指當特征屬性服從多項分布,從而,對于每個類別y,參數為???其中n為特征屬性數目,那么?
?的概率為?
?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
貝葉斯網絡
把某個研究系統中涉及到的隨機變量,根據是否條件獨立繪制在一個有向圖中,就形成了貝葉斯網絡。
貝葉斯網絡(Bayesian Network),又稱有向無環圖模型(directed acyclic graphical model,DAG),是一種概率圖模型,根據概率圖的拓撲結構,考察一組隨機變量??及其N組條件概率分布(Conditional Probabililty Distributions,CPD)的性質。
當多個特征屬性之間存在著某種相關關系的時候,使用樸素貝葉斯算法就沒法解決這類問題,那么貝葉斯網絡就是解決這類應用場景的一個非常好的算法。
一般而言,貝葉斯網絡的有向無環圖中的節點表示隨機變量,可以是可觀察到的變量,或隱變量、未知參數等等。連接兩個節點之間的箭頭代表兩個隨機變量之間的因果關系(也就是這兩個隨機變量之間非條件獨立),如果兩個節點間以一個單箭頭連接在一起,表示其中一個節點是“因”,另外一個是“果”,從而兩節點之間就會產生一個條件概率值。每個節點在給定其直接前驅的時候,條件獨立于其后繼。
貝葉斯網絡的關鍵方法是圖模型,構建一個圖模型我們需要把具有因果聯系的各個變量用箭頭連在一起。貝葉斯網絡的有向無環圖中的節點表示隨機變量。連接兩個節點的箭頭代表此兩個隨機變量是具有因果關系的。貝葉斯網絡是模擬人的認知思維推理模式的,用一組條件概率以及有向無環圖對不確定性因果推理關系建模。
最簡單的貝葉斯網絡
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

全連接貝葉斯網絡
每一對節點之間都有邊連接
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

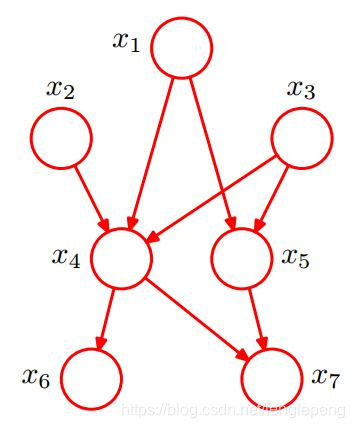
一般化的貝葉斯網絡
獨立?
??和?
在給定條件下獨立?
?的聯合分布為:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
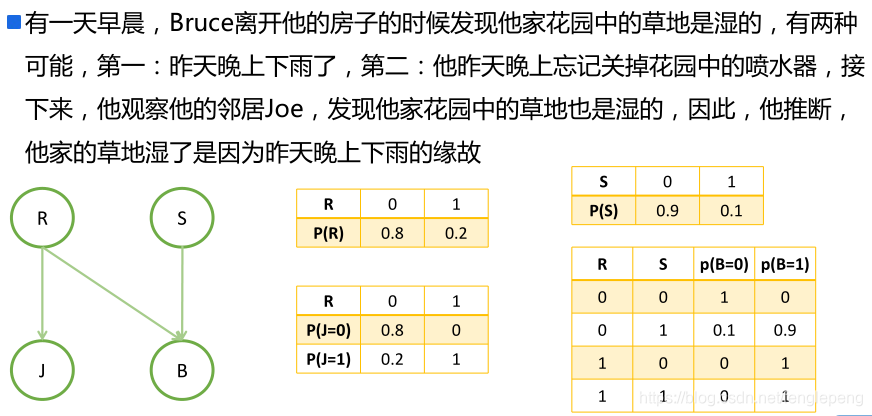
?案例




--受傷的總是我)







!!!...)
)




)

-------輸入映射(含面試題))