神經網絡的一種求解W的算法，分為信號“正向傳播(FP)”求損失，“反向傳播(BP)”回傳誤差；根據誤差值修改每層的權重，繼續迭代。

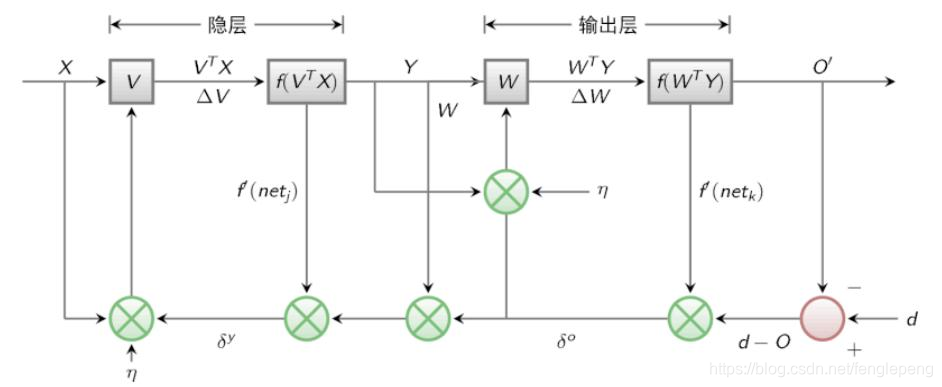
BP算法也叫做δ算法。以三層的感知器為例（假定現在隱層和輸出層均存在相同類型的激活函數）

• 隱層 y?= f(x * v)
• 輸出層 o = f(f(y) * w)
• 輸入層誤差:
• 隱層誤差:? ?
• 輸入層誤差:

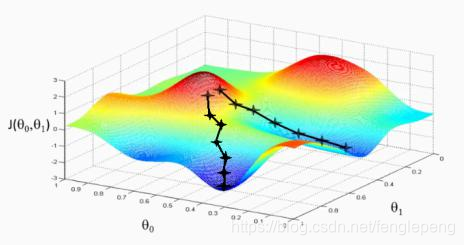
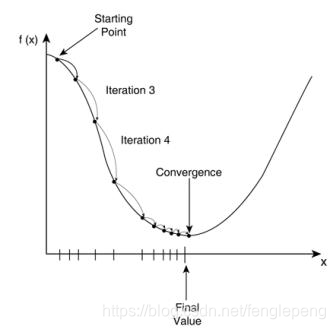
誤差E有了，那么為了使誤差越來越小，可以采用隨機梯度下降的方式進行ω和υ的求解，即求得ω和υ使得誤差E最小

BP算法的例子

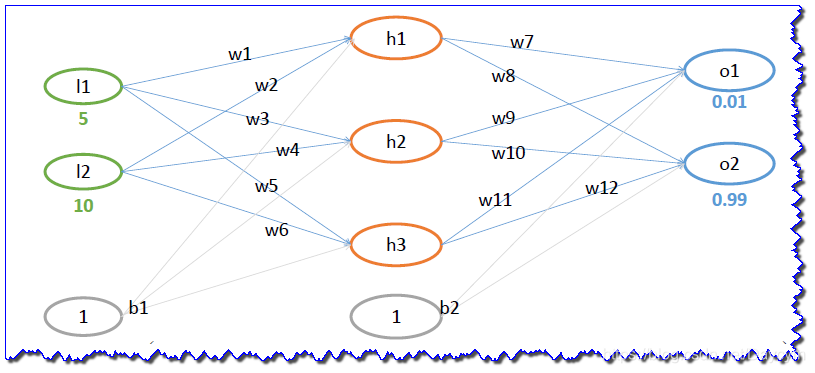
• 初始值：w(0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65)，? ?b(0.35,0.65)
• 輸出值：O=(0.01,0.99)
• 學習率：η=0.5?
• 假設隱層和輸出層都使用 sigmoid 激活函數

1、FP過程

先求out

同理可以得到：

同理可以得到：

輸出層誤差表示如下：

2、BP 過程

輸出層到第二層隱層，以求 ??為例：

下面我們分別求上式的三個部分，其中第一部分：

第二分部因為：

第三部分,因為：

最終得到：

更新??的值：

同理可以求出：

?

第二層隱層到第一層隱層，以求??為例：

下面我們分別計算，第一部分：

其中：

注意：這里由于是反向傳播，此時要用到之前更新后的???的值

同理計算：

接著計算第二部分：

接著計算第三部分：

最終整合起來：

于是更新 ：

同理求出：

以上是第一次迭代，經過多次迭代，最終的誤差會越來越小

上圖可以看出，當迭代1000次時，輸出為 O=(0.022971,0.977675) 和原本的 O=(0.01,0.99) 比較接近了。

python代碼

https://github.com/flepeng/code/blob/master/DL/bp_demo.py

import numpy as np# 初始值
w = [0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65]
# 偏置項b不進行更新
b = [0.35, 0.65]l = [5, 10]# sigmoid函數
def sigmoid(z):return 1.0 / (1 + np.exp(-z))def f1(w, b, l):# 前向傳播，計算結果值h1 = sigmoid(w[0] * l[0] + w[1] * l[1] + b[0])h2 = sigmoid(w[2] * l[0] + w[3] * l[1] + b[0])h3 = sigmoid(w[4] * l[0] + w[5] * l[1] + b[0])o1 = sigmoid(w[6] * h1 + w[8] * h2 + w[10] * h3 + b[1])o2 = sigmoid(w[7] * h1 + w[9] * h2 + w[11] * h3 + b[1])# 后向傳播，更新w# 輸出層到第二層隱層，前兩項# 公式中的第一部分-(0.01 - o1)，第二部分o1 * (l - o1)t1 = -(0.01 - o1) * o1 * (l - o1)# 第二層隱層到第一層隱層，前兩項t2 = -(0.99 - o2) * o2 * (l - o2)# t1*第三部分，即輸出層到第二層隱層的參數梯度w[6] = w[6] - 0.5 * (t1 * h1)w[8] = w[8] - 0.5 * (t1 * h2)w[10] = w[10] - 0.5 * (t1 * h3)w[7] = w[7] - 0.5 * (t2 * h1)w[9] = w[9] - 0.5 * (t2 * h2)w[11] = w[11] - 0.5 * (t2 * h3)# (t1 * w[6] + t2 * w[7])對于公式()中的兩項，h1 * (1 - h1)對于第二項，l[0]對應第三項w[0] = w[0] - 0.5 * (t1 * w[6] + t2 * w[7]) * h1 * (1 - h1) * l[0]w[1] = w[1] - 0.5 * (t1 * w[6] + t2 * w[7]) * h1 * (1 - h1) * l[1]w[2] = w[2] - 0.5 * (t1 * w[8] + t2 * w[9]) * h2 * (1 - h2) * l[0]w[3] = w[3] - 0.5 * (t1 * w[6] + t2 * w[9]) * h2 * (1 - h2) * l[1]w[4] = w[4] - 0.5 * (t1 * w[10] + t2 * w[11]) * h3 * (1 - h3) * l[0]w[5] = w[5] - 0.5 * (t1 * w[10] + t2 * w[11]) * h3 * (1 - h3) * l[1]return o1, o2, wfor i in range(1000):r1, r2, w = f1(w, b, l)print("第{}次迭代后，結果值為:({},{}),權重更新為:{}".format(i+1, r1, r2, w))

?