卷積神經網絡典型CNN

• LeNet：最早用于數字識別的CNN
• LeNet5：現在常說的一般就是LeNet5
• AlexNet：2012ILSVRC冠軍，遠超第二名的CNN，比LeNet更深，用多層小卷積疊加來替換單個的大卷積
• ZF Net：2013ILSVRC冠軍
• GoogLeNet：2014ILSVRC冠軍
• VGGNet：2014ILSVRC比賽中算法模型，效果率低于GoogleNet
• ResNet：2015ILSVRC冠軍，結構修正以適應更深層次的CNN訓練

卷積神經網絡典型CNN-LeNet

卷積神經網絡典型CNN-LeNet5

網絡結構

C1層是一個卷積層（卷積+激勵）

• input：1*32*32
• filter：1*5*5
• stripe：1?? ??? ??? ??? ?
• padding：0?? ??? ??? ??? ?
• filter size/depth：6?? ??? ??? ??? ?
• output：6*28*28?? ??? ??? ??? ?
• 神經元數目：6*28*28?? ??? ??? ??? ?
• 參數個數：(1*5*5+1)*6=156。每個特征圖內共享參數，因此參數總數：共（5*5+1）*6=156個參數
• 連接方式：普通的卷積連接方式?? ?
• 每個卷積神經元的參數數目：5*5=25個weight參數和一個bias參數
• 鏈接數目：（5*5+1）*6*（28*28）=122304個鏈接

S2層是一個下采樣層（池化）

• input：6*28*28
• filter：2*2
• padding：0
• stripe：2
• output：6*14*14。每個圖中的每個單元與C1特征圖中的一個2*2鄰域相連接，不重疊。因此，S2中每個特征圖的大小是C1中的特征圖大小的1/4
• 神經元數目：6*14*14
• 參數個數：0?? ??? ??? ?
• 連接方式：普通的最大池化方式

=========================================================================

現在 lenet5 多用改進的池化，池化方式如下

• S2層每個單元的4個輸入相加，乘以一個可訓練參數w，再加上一個可訓練偏置b，結果通過sigmoid函數計算
• 連接數：（2*2+1）*1*14*14*6=5880個
• 參數共享：每個特征圖內共享參數，因此有2*6=12個可訓練參數

C3層是一個卷積層（卷積+激勵）

• input：6*14*14?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ?
• filter：?*5*5?? ?6*5*5?? ??? ??? ??? ??? ??? ??? ??? ??? ?
• stripe：1?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ?
• padding：0?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ?
• filter size/depth：16?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ?
• output：16*10*10? ? ? ? ? ?
• 神經元數目：16*10*10?? ??? ??? ??? ??? ??? ??? ??? ??? ??? ?
• 參數個數：(3*5*5+1)*6+(4*5*5+1)*9+(6*5*5+1)*1=1516?? ??? ??? ??? ??? ??? ??? ??? ??? ?
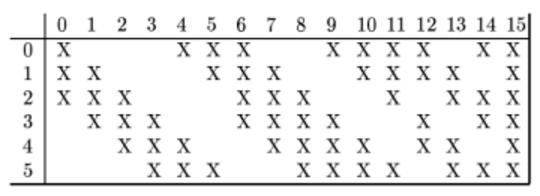
• 連接方式(S2->C3)?? ?不是普通的卷積操作，是卷積操作的變種。"最終輸出的16個fetaure map中，對應的前六個卷積核是和s2中輸出的六個feature map中的任意3個feature map做卷積，中間九個卷積核是和s2中輸出的六個feature map中的任意4個feature map做卷積，最后一個卷積核是和六個feature map做卷積"。
  • 好處：
    • 1. 不需要使用全部的feature map，這樣有連接的feature map的連接數/參數數量可以保持在一定范圍，直白來講：相對于傳統的卷積操作，降低了網絡的參數數據量
    • 2. 可以打破網絡的對稱結構，不同的卷積核可以得到不同的特征信息
  • 

S4層是一個下采樣層（池化）

• input:16*10*10
• filter:2*2
• padding:0
• stripe:2
• output:16*5*5
• 神經元數目:16*5*5
• 參數個數:0
• 連接方式:普通的最大池化方式

=========================================================================

現在 lenet5 多用改進的池化，池化方式如下

• S4層每個單元的4個輸入相加，乘以一個可訓練參數w，再加上一個可訓練偏置b，結果通過sigmoid函數計算
• 連接數：（2*2+1）*5*5*16=2000個
• 參數共享：特征圖內共享參數，每個特征圖中的每個神經元需要1個因子和一個偏置，因此有2*16個可訓練參數。

C5層是一個卷積層（卷積+激勵）

• input：16*5*5
• filter：16*5*5（沒有共享卷積核）
• stripe：1
• padding：0
• filter size/depth：120
• output：120*1*1
• 神經元數目：120*1*1
• 參數個數：(16*5*5+1)*120=48120
• 連接數：(16*5*5+1)*120=48120
• 連接方式:普通的卷積操作。好處、作用:當網絡結構不變，如果輸入的大小發生變化，那么C4的輸出就不是120啦。120個神經元，可以看作120個特征圖，每張特征圖的大小為1*1，每個單元與S4層的全部16個單元的5*5鄰域相連（S4和C5之間的全連接）

F6層是一個全連接層

• input：120
• output：84
• 神經元數目：84
• 參數個數：(120+1)*84=10164
• 連接數：（120+1）*84=10164
• 有84個單元（之所以選這個數字的原因來自于輸出層的設計），與C5層全連接。84：stylized image：7*12
• 

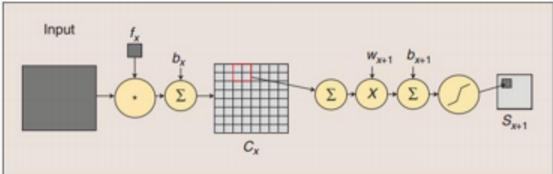
輸出層采用歐氏徑向基函數單元

• input：84
• output：10
• 神經元數目：10
• 參數數目：84*10=840
• 給定一個輸入模式，損失函數應能使得F6的配置與RBF參數向量（即模式的期望分類）足夠接近。
• 每類一個單元，每個單元連接84個輸入；每個輸出RBF單元計算輸入向量和參數向量之間的歐式距離。
• RBF輸出可以被理解為F6層配置空間的高斯分布的對數似然【-log-likelihood】

卷積神經網絡CNN性能演進歷程