前面我們說了CNN的一般層次結構, 每個層的作用及其參數的優缺點等內容.深度學習之卷積神經網絡(Convolutional Neural Networks, CNN)_fenglepeng的博客-CSDN博客?
一 CNN參數初始化及參數學習方法
和機器學習很多算法一樣, CNN在進行訓練之前也要進行參數的初始化操作. 我們知道, 在機器學習中的參數值一般都是隨機給定的. 但是, 這CNN的參數初始化又和機器學習中有所不同.?
1.1 W的初始化
由于CNN 中的參數更新的過程一般是通過BP算法實現的,再由前面我們在深度學習之BP算法一文中得到的BP算法參數更新公式可以發現, 參數更新過程中卷積核(權重值W)參與了連乘運算,因此一定不能初始化W = 0, 否則參數W無法更新.
另外考慮到太大(小)的W值可能導致梯度下降太快(慢), 一般選擇很小的隨機數, 且要求w為服從均值為0, 方差未知(建議選擇2/n, n為權重的個數)的正態分布的隨機序列.
1.2 b的初始化
一般直接設置為0,在存在ReLU激活函數的網絡中,也可以考慮設置為一個很小的數字.
1.3 CNN模型參數學習方法
CNN中的參數學習方法主要是BP算法.
前面我們知道,?BP算法的關鍵在于反向傳播時的鏈式求導求得誤差值?. 然后使用梯度下降的方法進行參數W和b的更新.
二 CNN過擬合

神經網絡的學習能力受神經元數目以及神經網絡層次的影響,神經元數目越大,神經網絡層次越高,那么神經網絡的學習能力越強,那么就有可能出現過擬合的問題;(通俗來講:神經網絡的空間表達能力變得更緊豐富了)
CNN是通過卷積核對樣本進行特征提取的, 當特征提取過多(即學習到了不重要的特征)就回造成過擬合現象的發生, 這里主要介紹兩種解決過擬合的方法, 分別為正則化和Dropout.
2.1 正則化
和機器學習一樣, 通過在損失函數加上L1,L2正則項可以有效地防止過擬合的問題.
?2.2 Dropout
一般情況下,對于同一組訓練數據,利用不同的神經網絡訓練之后,求其輸出的平均值可以減少overfitting。Dropout就是利用這個原理,每次丟掉一半左右的隱藏層神經元,相當于在不同的神經網絡上進行訓練,這樣就減少了神經元之間的依賴性,即每個神經元不能依賴于某幾個其它的神經元(指層與層之間相連接的神經元),使神經網絡更加能學習到與其它神經元之間的更加健壯robust(魯棒性)的特征。另外Dropout不僅減少overfitting,還能提高準確率。?

Dropout通過隨機刪除神經網絡中的神經元來解決overfitting問題,在每次迭代的時候,只使用部分神經元訓練模型獲取W和d的值. 具體的可以參見PDF文檔http://nooverfit.com/wp/wp-content/uploads/2016/07/Dropout-A-Simple-Way-to-Prevent-Neural-Networks-from-Overfitting.pdf
p=0.5 # dropout保留一個神經元存活的概率def train_out(X):# H1 = np.maximum(0,np.dot(ω1,X)+b1) # 第一次dropout,注意做了一次除以P。U1 = (np.random.rand(*H1.shape)<p)/p # [0. 2. 2. 2. 0. 0. 2. 2. 0. 0.]# drop轉換為0或者原始值H1 *= U1H2 = np.maximum(0,np.dot(ω2,H1)+b2)# 第二次dropout,其中除以P。U2 =(np.random.rand(*H2.shape)<p)/p# 類似上方H2 *= U2out = np.dot(ω3,H2)+b3 # BP操作:計算梯度,參數更新def predict(X):#直接前向計算,不乘以PH1=np.maximum(0,np.dot(ω1,X)+b1)H2=np.maximum(0,np.dot(ω2,H1)+b2)out=np.dot(ω3,H2)+b3
2.3 方案選擇
- 一般都可以使用Dropout解決過擬合問題
- 回歸算法中使用L2范數相比于Softmax分類器,更加難以優化。對于回歸問題,首先考慮是否可以轉化為分類問題,比如:用戶對于商品的評分,可以考慮將得分結果分成1~5分,這樣就變成了一個分類問題。如果實在沒法轉化為分類問題的,那么使用L2范數的時候要非常小心,比如在L2范數之前不要使用Dropout。
- 一般建議使用L2范數或者Dropout來減少神經網絡的過擬合
?
三、卷積神經網絡訓練算法
和一般的機器學習算法一樣,需要先定義Loss Function,衡量預測值和實際值之間的誤差,一般使用平方和誤差公式找到最小損失函數的W和b的值,CNN中常使用的是SGD其實就是一般深度學習中的BP算法;SGD需要計算W和b的偏導,BP算法就是計算偏導用的,BP算法的核心是求導鏈式法則。
在神經網絡中一般采用Mini-batch SGD,主要包括以下四個步驟的循環:
- 采樣一個batch的數據
- 前向計算損失loss
- 反向傳播計算梯度(一個batch上所有樣本的梯度和)
- 利用梯度更新權重參數
使用BP算法逐級求解△ω和△b的值。
根據SGD隨機梯度下降迭代更新ω和b。
四、池化層誤差反向傳播
Maxpool最大池化層反向傳播:除最大值處繼承上層梯度外,其他位置置零。

平均池化:將殘差均分為2×2=4份,傳遞到前面小區域的4個單元中。

def max_pool_backward_naive(dout,cache):x,pool_param=cacheHH,WW=pool_param['pool_height'],pool_param['pool_width']s=pool_param['stride']N,C,H,W=x.shapeH_new=1+(H-HH)/sW_new=1+(W-WW)/sdx=np.zeros_like(x)for i in range(N):for j in range(C):for k in range(H_new):for l in range(W_new):windows=x[i,j,k*s:HH+k*s,l*s:WW+l*s]m=np.max(windows)dx[i,j,k*s:HH+k*s,l*s:WW+l*s]=(windows==m)*dout[i,j,k,l]return dx梯度下降
梯度下降是常用的卷積神經網絡模型參數求解方法,根據每次參數更新使用樣本數量的多少,可以分為以下三類:
- 批量梯度下降(batch gradient descent,BGD);
- 小批量梯度下降(mini-batch gradient descent,MBGD);
- 隨機梯度下降(stochastic gradient descent,SGD)。
詳細請參考:機器學習之梯度下降法(GD)和坐標軸下降法(CD)
深度學習超參數
學習率(Learning Rate )
學習率被定義為每次迭代中成本函數中最小化的量。也即下降到成本函數的最小值的速率是學習率,它是可變的。從梯度下降算法的角度來說,通過選擇合適的學習率,可以使梯度下降法得到更好的性能。
一般常用的學習率有0.00001,0.0001,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10
學習率調整策略
- fixed固定策略,學習率始終是一個固定值。
- step 均勻分步策略,如果設置為step,則還需要設置一個stepsize, 返回base_lr * gamma (floor(iter / stepsize)) 其中iter表示當前的迭代次數。floor(9.9)=9, 其功能是“下取整”。
- base_lr * gamma ?iter , iter為當前迭代次數。
- multistep 多分步或不均勻分步。剛開始訓練網絡時學習率一般設置較高,這樣loss和accuracy下降很快,一般前200000次兩者下降較快,后面可能就需要我們使用較小的學習率了。step策略由于過于平均,而loss和accuracy的下降率在整個訓練過程中又是一個不平均的過程,因此有時不是很合適。fixed手工調節起來又很麻煩,這時multistep可能就會派上用場了。multistep還需要設置一個stepvalue。這個參數和step很相似,step是均勻等間隔變化,而multistep則是根據 stepvalue值變化
- multistep設置示例(caffe)
base_lr: 0.01
momentum: 0.9
weight_decay: 0.0005
# The learning rate policy
lr_policy: "multistep"
gamma: 0.9
stepvalue: 5000
stepvalue: 7000
stepvalue: 8000
stepvalue: 9000
stepvalue: 9500- poly: 學習率進行多項式誤差, 返回 base_lr *(1 - iter/max_iter) ?power
深度學習訓練過程
過擬合
過擬合就是模型把數據學習的太徹底,以至于把噪聲數據的特征也學習到了,這樣就會導致在后期測試的時候不能夠很好地識別數據,即不能正確的分類,模型泛化能力太差。
欠擬合
欠擬合模型沒有很好地捕捉到數據特征,不能夠很好地擬合數據。
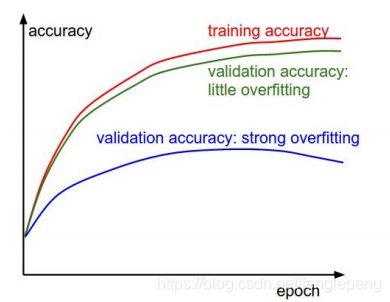
誤差的變化

根據特征的層來調整參數
左圖很粗糙,顯示不出底層特征,可能是因為網絡不收斂或者學習速率設置不好或者是因為懲罰因子設置的太小。 右圖合理,特征多樣,比較干凈、平滑

https://www.microsoft.com/zh-cn/download/details.aspx?id=48145&751be11f-ede8-5a0c-058c-2ee190a24fa6=True







)











