樹

?

樹的定義：樹(Tree)是 n(n≥0)個結點的有限集。若 n=0，稱為空樹；若 n > 0，則它滿足如下兩個條件： ?

(1) ?有且僅有一個特定的稱為根 (Root) 的結點； ?

(2) ?其余結點可分為 m (m≥0) 個互不相交的有限集 T1, T2, T3, …, Tm， 其中每一個集合本身又是一棵樹，并稱為根的子樹 (SubTree)。

顯然，樹的定義是一個遞歸的定義。

樹的一些術語：

• 結點的度（Degree）：結點的子樹個數；
• 樹的度：樹的所有結點中最大的度數；
• 葉結點（Leaf）：度為0的結點；
• 父結點（Parent）：有子樹的結點是其子樹的根節點的父結點；
• 子結點/孩子結點（Child）：若A結點是B結點的父結點，則稱B結點是A結點的子結點；
• 兄弟結點（Sibling）：具有同一個父結點的各結點彼此是兄弟結點；
• 路徑和路徑長度：從結點n1到nk的路徑為一個結點序列n1，n2，...，nk。ni是ni+1的父結點。路徑所包含邊的個數為路徑的長度；
• 祖先結點（Ancestor）：沿樹根到某一結點路徑上的所有結點都是這個結點的祖先結點；
• 子孫結點（Descendant）：某一結點的子樹中的所有結點是這個結點的子孫；
• 結點的層次（Level）：規定根結點在1層，其他任一結點的層數是其父結點的層數加1；
• 樹的深度（Depth）：樹中所有結點中的最大層次是這棵樹的深度；

將樹中節點的各子樹看成從左至右是有次序的（即不能互換），則稱為該樹是有序樹，否則稱為無序樹。

森林(forest)是 m (m≥0) 棵互不相交的樹的集合。

?

二叉樹

?

在計算機科學中，二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”（left subtree）和“右子樹”（right subtree）。二叉樹常被用于實現二叉查找樹和二叉堆。

?

雖然二叉樹與樹概念不同，但有關樹的基本術語對二叉樹都適用。

?

二叉樹結點的子樹要區分左子樹和右子樹，即使只有一 棵子樹也要進行區分，說明它是左子樹，還是右子樹。樹當 結點只有一個孩子時，就無須區分它是左還是右。

?

注意：盡管二叉樹與樹有許多相似之處，但二叉樹不是樹的特殊情形。

一些性質：

在二叉樹的第 i 層上至多有? 個結點 (i ≥1)。

證明：每個節點至多兩個孩子，每一層至多比上一層多一倍的結點，根為1.

?

深度為 k 的二叉樹至多有 個結點（k ≥1)。

證明：把每一層最大節點加起來即可

?

對任何一棵二叉樹 T，如果其葉子數為 n0，度為 2的結點數為 n2，則 n0 = n2 + 1。

證明：對于一個只有根的樹，n0 = n2 + 1成立。1=0+1

我們把一個葉子節點換成度為2的結點：

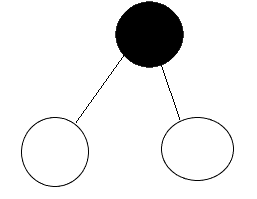
黑色節點原來為葉子節點

我們發現，度為2的結點數加1（黑色節點）；葉子節點數加1（原來的去掉，新增兩個）；對于式子n0 = n2 + 1沒影響，還是成立。

?

我們把葉子節點換成度為1的結點，比如沒有右孩子。

我們發現，度為2的結點數沒變。葉子節點數沒變（減了一個加了一個）

所以，不管你怎么換，公式都成立。（佛系證明）

?

?