第一次見這個題，看時間小于O(N)。。。。。

只能是二分啊。

但是怎么二分，條件是什么，真的想不到。

?

后來知道了，我們要找最深一層最右邊那個結點。借此確定結點個數。

?

我們知道，滿二叉樹的結點個數和深度是有公式的，那么我們找到最后一層最右邊的結點，其實就可以確定結點個數。

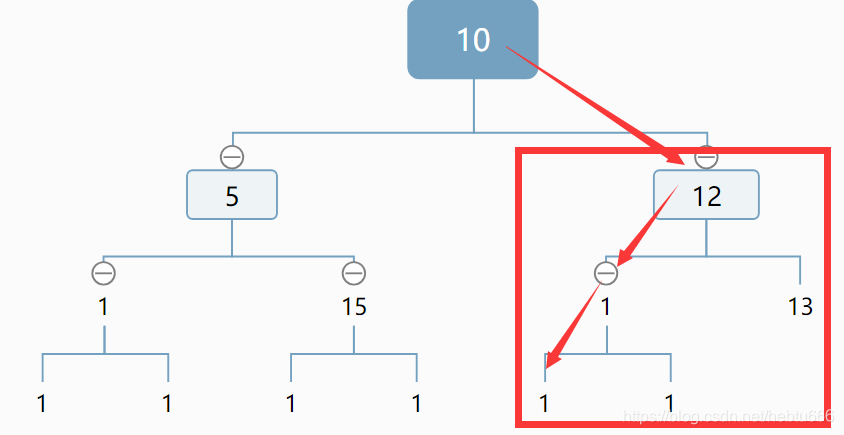
目標：找箭頭指向的結點。

?

我們采用二分法：

1）找到右子樹的最左結點

如果右子樹深度為3（4-1），說明圖中最后的1是存在的（說明最后一行最右結點一定來自右子樹），否則

右子樹深度為2！=4-1，不存在最后一行的結點。（說明最后一行最右結點一定來自左子樹）.

?

判斷之后，如果是這種情況，我們排除了左子樹，計算排除的結點個數（如圖），并對右子樹做相同的處理。

更新結點數（未被框起的部分，滿二叉樹公式+1）+1是根結點

對方框內重復此過程。

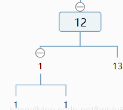
我們繼續看右子樹，發現右子樹深度為1！=3-1.

說明最深層最右結點來自于左子樹。所以對左子樹重復上述過程

我們發現，右子樹深度=1=2（整棵樹深度）-1，說明最深層最右結點來自于右子樹，所以對右子樹重復此過程。

最終找到它

?

我們再回憶一下過程：

?

1）找到右子樹最左節點，確定了深度，對右子樹重復。

2）找到右子樹最左節點，確定了深度，對左子樹重復。

3）找到右子樹最左節點，確定了深度，對右子樹重復。

4）找到

?

過程中可以

1）把排除的部分全部加起來，

2）也可以記錄每次的選擇（向左還是向右），最終100010這種字符，其實就是最后一層的結點個數。

?

貼上方法1的全部代碼：

public class Demo {public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}
//返回結點個數public static int nodeNum(Node head) {if (head == null) {return 0;}return bs(head, 1, mostLeftLevel(head, 1));}
//返回根為node，當前層數為l，總深度為h的結點個數public static int bs(Node node, int l, int h) {if (l == h) {return 1;}if (mostLeftLevel(node.right, l + 1) == h) {             //右子樹最深一行最左為空return (1 << (h - l)) + bs(node.right, l + 1, h);    //右bs+左子樹結點個數} else {                                                 //右子樹最深一行最左不為空return (1 << (h - l - 1)) + bs(node.left, l + 1, h);//左bs+右子樹結點個數}}
//計算樹的高度public static int mostLeftLevel(Node node, int level) {while (node != null) {level++;node = node.left;}return level - 1;}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.left.right = new Node(5);head.right.left = new Node(6);System.out.println(nodeNum(head));}}

?