數據結構–拓撲排序

AOV?

$AOV?$(Activity On Vertex NetWork，?頂點表示活動的?)：
?$DAG圖$（有向?環圖）表示?個?程。頂點表示活動，有向邊$<V_i,V_j>$表示活動Vi必須先于活動$V_j$進?

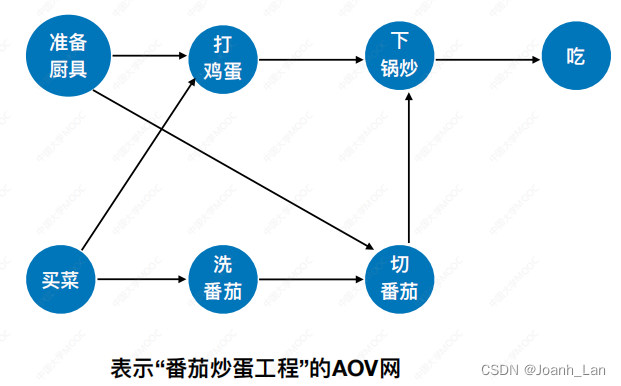
$注：如果圖中存在環路就不是AOV網$

DAG圖是指有向無環圖（Directed Acyclic Graph），是一種有向圖的特殊形式。它由一些有向邊連接的節點組成，并且不存在任何形式的環。換句話說，從任何一個節點出發，沿著有向邊的方向無法經過一系列的節點再回到原始節點。DAG圖常用于表示一些具有依賴關系的任務或事件，其中每個節點表示一個任務或事件，有向邊表示任務或事件之間的依賴關系。DAG圖在計算機科學和工程中有廣泛的應用，例如任務調度、編譯器優化、數據流分析等領域。

拓撲排序

$拓撲排序$：在圖論中，由?個$有向?環圖$的頂點組成的序列，當且僅當滿?下列條件時，稱為該圖的?個拓撲排序：
① 每個頂點出現且只出現?次。
② 若頂點A在序列中排在頂點B的前?，則在圖中不存在從頂點B到頂點A的路徑。或定義為：拓撲排序是對有向?環圖的頂點的?種排序，它使得若存在?條從頂點A到頂點B的路徑，則在排序中頂點B出現在頂點A的后?。每個AOV?都有?個或多個拓撲排序序列。

上圖其中一個拓撲排序：

拓撲排序的實現：

① 從AOV?中選擇?個沒有前驅的頂點并輸出。
② 從?中刪除該頂點和所有以它為起點的有向邊。
③ 重復①和②直到當前的AOV?為空或當前?中不存在?前驅的頂點為?。

$注：拓撲排序序列可能有多個$

拓撲排序代碼實現

王道書上代碼

個人code

#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool topsort()
{int tt = -1, hh = 0;for(int i = 1; i <= n; i++)if(!d[i])q[++tt] = i;while(hh <= tt){int t = q[hh++];for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];d[j]--;if(!d[j]) q[++tt] = j;}}return tt == n - 1;
}
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0; i < n; i++){int a, b;cin >> a >> b;add(a, b);d[b]++;}if(topsort()){for(int i = 0; i < n; i++)cout << q[i] << ' ';cout << endl;}else cout << "-1" << endl;return 0;
}

判斷是否存在拓撲序

時間復雜度 O(n + m), n 表示點數，m表示邊數
bool topsort()
{int hh = 0, tt = -1;// d[i] 存儲點i的?度for (int i = 1; i <= n; i ++ )if (!d[i])q[ ++ tt] = i;while (hh <= tt){int t = q[hh ++ ];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (-- d[j] == 0)q[ ++ tt] = j;}}// 如果所有點都?隊了，說明存在拓撲序列；否則不存在拓撲序列。return tt == n - 1;
}

逆拓撲排序

對?個AOV?，如果采?下列步驟進?排序，則稱之為$逆拓撲排序$：
① 從AOV?中選擇?個沒有后繼（$出度為0$）的頂點并輸出。
② 從?中刪除該頂點和所有以它為終點的有向邊。
③ 重復①和②直到當前的AOV?為空。

其中一個逆拓撲排序

逆拓撲排序代碼實現

逆拓撲排序的實現（DFS算法）

DFS判斷是否有環：

int vis[N], cnt; // timestamp
int per[N];
bool cyc[N];// 標記
void dfs(int u) //找環 & 標記環
{vis[u] = ++cnt;for (auto v : g[u]){if (per[u] == v)continue;if (!vis[v]){per[v] = u;dfs(v);}else if (vis[u] > vis[v]){for (int i = u; i != v; i = per[i])cyc[i] = true;cyc[v] = true;}}
}

如果單純判斷是否有環，只需要引進父結點（fa）
dfs(u,fa)
如果 u == fa 則存在環

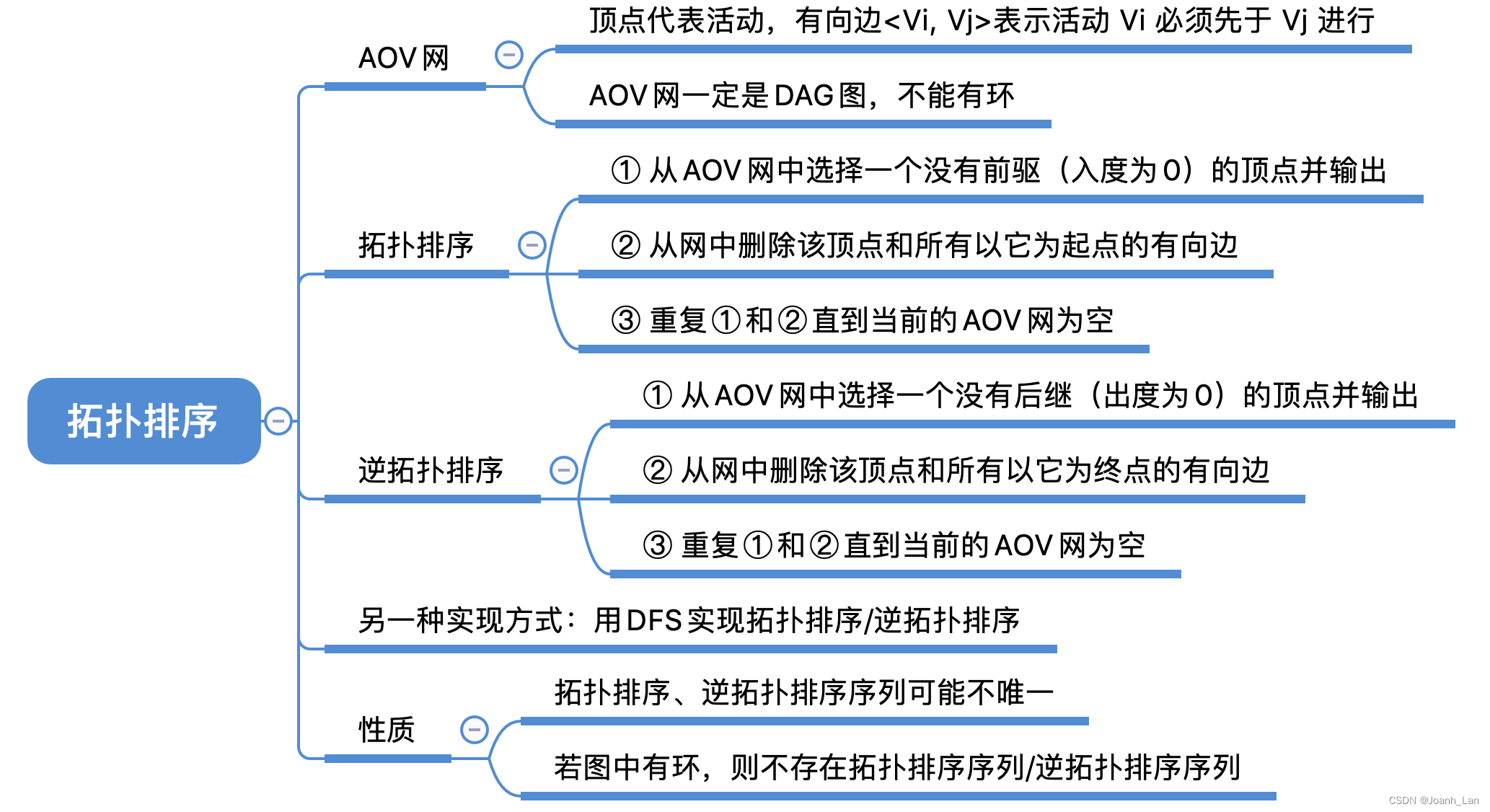
知識點回顧與重要考點