注：此文只在個人總結 labuladong 動態規劃框架，僅限于學習交流，版權歸原作者所有；

本文是兩年前發的 動態規劃答疑篇open in new window 的修訂版，根據我的不斷學習總結以及讀者的評論反饋，我給擴展了更多內容，力求使本文成為繼 動態規劃核心套路框架 之后的一篇全面答疑文章。以下是正文。

這篇文章就給你講明白以下幾個問題：

1、到底什么才叫「最優子結構」，和動態規劃什么關系。

2、如何判斷一個問題是動態規劃問題，即如何看出是否存在重疊子問題。

3、為什么經常看到將 dp 數組的大小設置為 n + 1 而不是 n。

4、為什么動態規劃遍歷 dp 數組的方式五花八門，有的正著遍歷，有的倒著遍歷，有的斜著遍歷。

注：

1. 可以通過子問題推導出原問題就是證明有最優子結構，而最優子結構 + 重疊子問題 = 動態規劃；

一、最優子結構詳解

「最優子結構」是某些問題的一種特定性質，并不是動態規劃問題專有的。也就是說，很多問題其實都具有最優子結構，只是其中大部分不具有重疊子問題，所以我們不把它們歸為動態規劃系列問題而已。

我先舉個很容易理解的例子：假設你們學校有 10 個班，你已經計算出了每個班的最高考試成績。那么現在我要求你計算全校最高的成績，你會不會算？當然會，而且你不用重新遍歷全校學生的分數進行比較，而是只要在這 10 個最高成績中取最大的就是全校的最高成績。

我給你提出的這個問題就符合最優子結構：可以從子問題的最優結果推出更大規模問題的最優結果。讓你算每個班的最優成績就是子問題，你知道所有子問題的答案后，就可以借此推出全校學生的最優成績這個規模更大的問題的答案。

你看，這么簡單的問題都有最優子結構性質，只是因為顯然沒有重疊子問題，所以我們簡單地求最值肯定用不出動態規劃。

再舉個例子：假設你們學校有 10 個班，你已知每個班的最大分數差（最高分和最低分的差值）。那么現在我讓你計算全校學生中的最大分數差，你會不會算？可以想辦法算，但是肯定不能通過已知的這 10 個班的最大分數差推到出來。因為這 10 個班的最大分數差不一定就包含全校學生的最大分數差，比如全校的最大分數差可能是 3 班的最高分和 6 班的最低分之差。

這次我給你提出的問題就不符合最優子結構，因為你沒辦通過每個班的最優值推出全校的最優值，沒辦法通過子問題的最優值推出規模更大的問題的最優值。前文 動態規劃詳解 說過，想滿足最優子結，子問題之間必須互相獨立。全校的最大分數差可能出現在兩個班之間，顯然子問題不獨立，所以這個問題本身不符合最優子結構。

那么遇到這種最優子結構失效情況，怎么辦？策略是：改造問題。對于最大分數差這個問題，我們不是沒辦法利用已知的每個班的分數差嗎，那我只能這樣寫一段暴力代碼：

int result = 0;
for (Student a : school) {for (Student b : school) {if (a is b) continue;result = max(result, |a.score - b.score|);}
}
return result;

改造問題，也就是把問題等價轉化：最大分數差，不就等價于最高分數和最低分數的差么，那不就是要求最高和最低分數么，不就是我們討論的第一個問題么，不就具有最優子結構了么？那現在改變思路，借助最優子結構解決最值問題，再回過頭解決最大分數差問題，是不是就高效多了？

當然，上面這個例子太簡單了，不過請讀者回顧一下，我們做動態規劃問題，是不是一直在求各種最值，本質跟我們舉的例子沒啥區別，無非需要處理一下重疊子問題。

前文不 同定義不同解法 和 高樓扔雞蛋問題 就展示了如何改造問題，不同的最優子結構，可能導致不同的解法和效率。

再舉個常見但也十分簡單的例子，求一棵二叉樹的最大值，不難吧（簡單起見，假設節點中的值都是非負數）：

int maxVal(TreeNode root) {if (root == null)return -1;int left = maxVal(root.left);int right = maxVal(root.right);return max(root.val, left, right);
}

你看這個問題也符合最優子結構，以 root 為根的樹的最大值，可以通過兩邊子樹（子問題）的最大值推導出來，結合剛才學校和班級的例子，很容易理解吧。

當然這也不是動態規劃問題，旨在說明，最優子結構并不是動態規劃獨有的一種性質，能求最值的問題大部分都具有這個性質；但反過來，最優子結構性質作為動態規劃問題的必要條件，一定是讓你求最值的，以后碰到那種惡心人的最值題，思路往動態規劃想就對了，這就是套路。

動態規劃不就是從最簡單的 base case 往后推導嗎，可以想象成一個鏈式反應，以小博大。但只有符合最優子結構的問題，才有發生這種鏈式反應的性質。

找最優子結構的過程，其實就是證明狀態轉移方程正確性的過程，方程符合最優子結構就可以寫暴力解了，寫出暴力解就可以看出有沒有重疊子問題了，有則優化，無則 OK。這也是套路，經常刷題的讀者應該能體會。

這里就不舉那些正宗動態規劃的例子了，讀者可以翻翻歷史文章，看看狀態轉移是如何遵循最優子結構的，這個話題就聊到這，下面再來看其他的動態規劃迷惑行為。

注：

1. 最優子結構只是動態規劃問題的必要條件，比如求二叉樹最大值，但是能求最值問題的大都具有最優子結構；
2. 動態規劃問題一定是讓求最值的；
3. 找最優子結構的過程，其實就是證明狀態轉移方程正確性的過程，方程符合最優子結構就可以寫暴力解了，寫出暴力解就可以看出有沒有重疊子問題了，有則優化，無則 OK。這也是套路，經常刷題的讀者應該能體會；

二、如何一眼看出重疊子問題

經常有讀者說：

看了前文 動態規劃核心套路，我知道了如何一步步優化動態規劃問題；

看了前文 動態規劃設計：數學歸納法，我知道了利用數學歸納法寫出暴力解（狀態轉移方程）。

但就算我寫出了暴力解，我很難判斷這個解法是否存在重疊子問題，從而無法確定是否可以運用備忘錄等方法去優化算法效率。

對于這個問題，其實我在動態規劃系列的文章中寫過幾次，在這里再統一總結一下吧。

首先，最簡單粗暴的方式就是畫圖，把遞歸樹畫出來，看看有沒有重復的節點。

比如最簡單的例子，動態規劃核心套路 中斐波那契數列的遞歸樹：

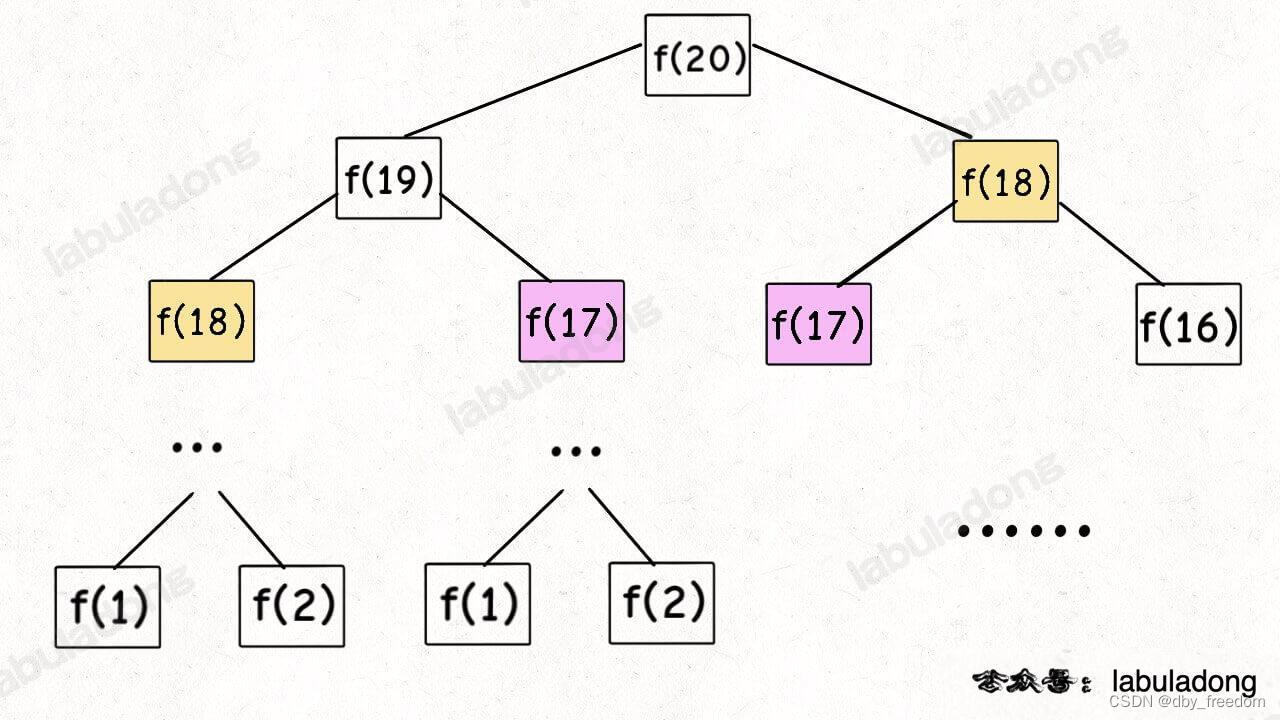
這棵遞歸樹很明顯存在重復的節點，所以我們可以通過備忘錄避免冗余計算。

但畢竟斐波那契數列問題太簡單了，實際的動態規劃問題比較復雜，比如二維甚至三維的動態規劃，當然也可以畫遞歸樹，但不免有些復雜。

比如在 最小路徑和問題 中，我們寫出了這樣一個暴力解法：

int dp(int[][] grid, int i, int j) {if (i == 0 && j == 0) {return grid[0][0];}if (i < 0 || j < 0) {return Integer.MAX_VALUE;}return Math.min(dp(grid, i - 1, j), dp(grid, i, j - 1)) + grid[i][j];
}

你不需要讀過前文，光看這個函數代碼就能看出來，該函數遞歸過程中參數 i, j 在不斷變化，即「狀態」是 (i, j) 的值，你是否可以判斷這個解法是否存在重疊子問題呢？

假設輸入的 i = 8, j = 7，二維狀態的遞歸樹如下圖，顯然出現了重疊子問題：

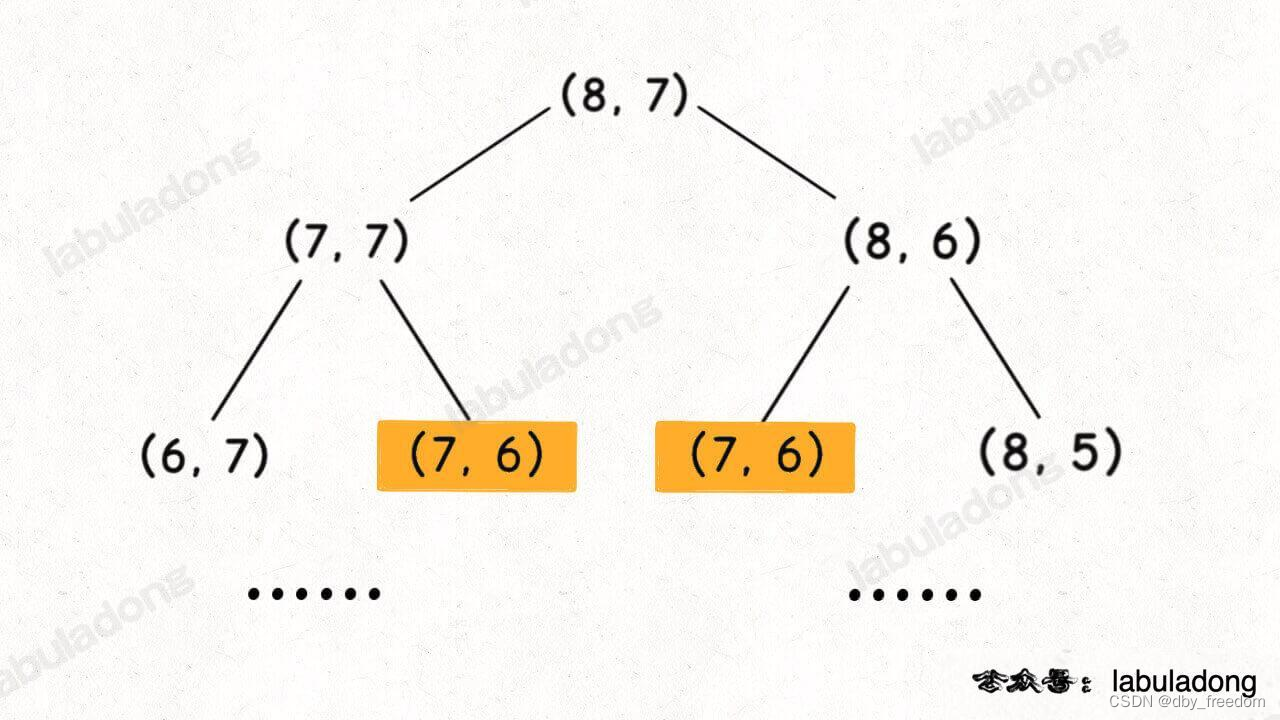
但稍加思考就可以知道，其實根本沒必要畫圖，可以通過遞歸框架直接判斷是否存在重疊子問題。

具體操作就是直接刪掉代碼細節，抽象出該解法的遞歸框架：

int dp(int[][] grid, int i, int j) {dp(grid, i - 1, j), // #1dp(grid, i, j - 1)  // #2
}

可以看到 i, j 的值在不斷減小，那么我問你一個問題：如果我想從狀態 (i, j) 轉移到 (i-1, j-1)，有幾種路徑？

顯然有兩種路徑，可以是 (i, j) -> #1 -> #2 或者 (i, j) -> #2 -> #1，不止一種，說明 (i-1, j-1) 會被多次計算，所以一定存在重疊子問題。

再舉個稍微復雜的例子，后文 正則表達式問題 的暴力解代碼：

bool dp(string& s, int i, string& p, int j) {int m = s.size(), n = p.size();if (j == n)  return i == m;if (i == m) {if ((n - j) % 2 == 1) return false;for (; j + 1 < n; j += 2) {if (p[j + 1] != '*') return false;}return true;}if (s[i] == p[j] || p[j] == '.') {if (j < n - 1 && p[j + 1] == '*') {return dp(s, i, p, j + 2)|| dp(s, i + 1, p, j);} else {return dp(s, i + 1, p, j + 1);}} else if (j < n - 1 && p[j + 1] == '*') {return dp(s, i, p, j + 2);}return false;
}

代碼有些復雜對吧，如果畫圖的話有些麻煩，但我們不畫圖，直接忽略所有細節代碼和條件分支，只抽象出遞歸框架：

bool dp(string& s, int i, string& p, int j) {dp(s, i, p, j + 2);     // #1dp(s, i + 1, p, j);     // #2dp(s, i + 1, p, j + 1); // #3
}

和上一題一樣，這個解法的「狀態」也是 (i, j) 的值，那么我繼續問你問題：如果我想從狀態 (i, j) 轉移到 (i+2, j+2)，有幾種路徑？

顯然，至少有兩條路徑：(i, j) -> #1 -> #2 -> #2 和 (i, j) -> #3 -> #3，這就說明這個解法存在巨量重疊子問題。

所以，不用畫圖就知道這個解法也存在重疊子問題，需要用備忘錄技巧去優化。

注：重疊子問題：最笨的方法是腦補一個遞歸樹，看有沒有重疊子問題；進一步可以通過遞歸框架判斷是否有子問題，有子問題就可以考慮使用備忘錄技巧去優化；

三、dp 數組的大小設置

比如說后文 編輯距離問題，我首先講的是自頂向下的遞歸解法，實現了這樣一個 dp 函數：

int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// 按照 dp 函數的定義，計算 s1 和 s2 的最小編輯距離return dp(s1, m - 1, s2, n - 1);
}// 定義：s1[0..i] 和 s2[0..j] 的最小編輯距離是 dp(s1, i, s2, j)
int dp(String s1, int i, String s2, int j) {// 處理 base caseif (i == -1) {return j + 1;}if (j == -1) {return i + 1;}// 進行狀態轉移if (s1.charAt(i) == s2.charAt(j)) {return dp(s1, i - 1, s2, j - 1);} else {return min(dp(s1, i, s2, j - 1) + 1,dp(s1, i - 1, s2, j) + 1,dp(s1, i - 1, s2, j - 1) + 1);}
}

然后改造成了自底向上的迭代解法：

int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// 定義：s1[0..i] 和 s2[0..j] 的最小編輯距離是 dp[i+1][j+1]int[][] dp = new int[m + 1][n + 1];// 初始化 base case for (int i = 1; i <= m; i++)dp[i][0] = i;for (int j = 1; j <= n; j++)dp[0][j] = j;// 自底向上求解for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 進行狀態轉移if (s1.charAt(i-1) == s2.charAt(j-1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1,dp[i][j - 1] + 1,dp[i - 1][j - 1] + 1);}}}// 按照 dp 數組的定義，存儲 s1 和 s2 的最小編輯距離return dp[m][n];
}

這兩種解法思路是完全相同的，但就有讀者提問，為什么迭代解法中的 dp 數組初始化大小要設置為 int[m+1][n+1]？為什么 s1[0..i] 和 s2[0..j] 的最小編輯距離要存儲在 dp[i+1][j+1] 中，有一位索引偏移？

能不能模仿 dp 函數的定義，把 dp 數組初始化為 int[m][n]，然后讓 s1[0..i] 和 s2[0..j] 的最小編輯距離要存儲在 dp[i][j] 中？

理論上，你怎么定義都可以，只要根據定義處理好 base case 就可以。

你看 dp 函數的定義，dp(s1, i, s2, j) 計算 s1[0..i] 和 s2[0..j] 的編輯距離，那么 i, j 等于 -1 時代表空串的 base case，所以函數開頭處理了這兩種特殊情況。

再看 dp 數組，你當然也可以定義 dp[i][j] 存儲 s1[0..i] 和 s2[0..j] 的編輯距離，但問題是 base case 怎么搞？索引怎么能是 -1 呢？

所以我們把 dp 數組初始化為 int[m+1][n+1]，讓索引整體偏移一位，把索引 0 留出來作為 base case 表示空串，然后定義 dp[i+1][j+1] 存儲 s1[0..i] 和 s2[0..j] 的編輯距離。

注：dp 數組大小到底如何定義，依據 base case 來定，比如編輯距離問題中，base case dp[0][0] 代表空串情況，因此 dp 數組需要設置為 dp[m+1][n+1]，把索引 0 留出來表示 base case 空串，做題時候，可以考慮下空串之類的情況再考慮設置 dp 數組大小；

四、dp 數組的遍歷方向

我相信讀者做動態規問題時，肯定會對 dp 數組的遍歷順序有些頭疼。我們拿二維 dp 數組來舉例，有時候我們是正向遍歷：

int[][] dp = new int[m][n];
for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)// 計算 dp[i][j]

有時候我們反向遍歷：

for (int i = m - 1; i >= 0; i--)for (int j = n - 1; j >= 0; j--)// 計算 dp[i][j]

有時候可能會斜向遍歷：

// 斜著遍歷數組
for (int l = 2; l <= n; l++) {for (int i = 0; i <= n - l; i++) {int j = l + i - 1;// 計算 dp[i][j]}
}

甚至更讓人迷惑的是，有時候發現正向反向遍歷都可以得到正確答案，比如我們在 團滅股票問題 中有的地方就正反皆可。

如果仔細觀察的話可以發現其中的原因，你只要把住兩點就行了：

1、遍歷的過程中，所需的狀態必須是已經計算出來的。

2、遍歷結束后，存儲結果的那個位置必須已經被計算出來。

注：

1. 遍歷開始時候，所需狀態必須已經計算出來；

2. 遍歷結束時候，存儲結果的位置必須已經計算出來；

下面來具體解釋上面兩個原則是什么意思。

比如編輯距離這個經典的問題，詳解見后文 編輯距離詳解，我們通過對 dp 數組的定義，確定了 base case 是 dp[..][0] 和 dp[0][..]，最終答案是 dp[m][n]；而且我們通過狀態轉移方程知道 dp[i][j] 需要從 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 轉移而來，如下圖：

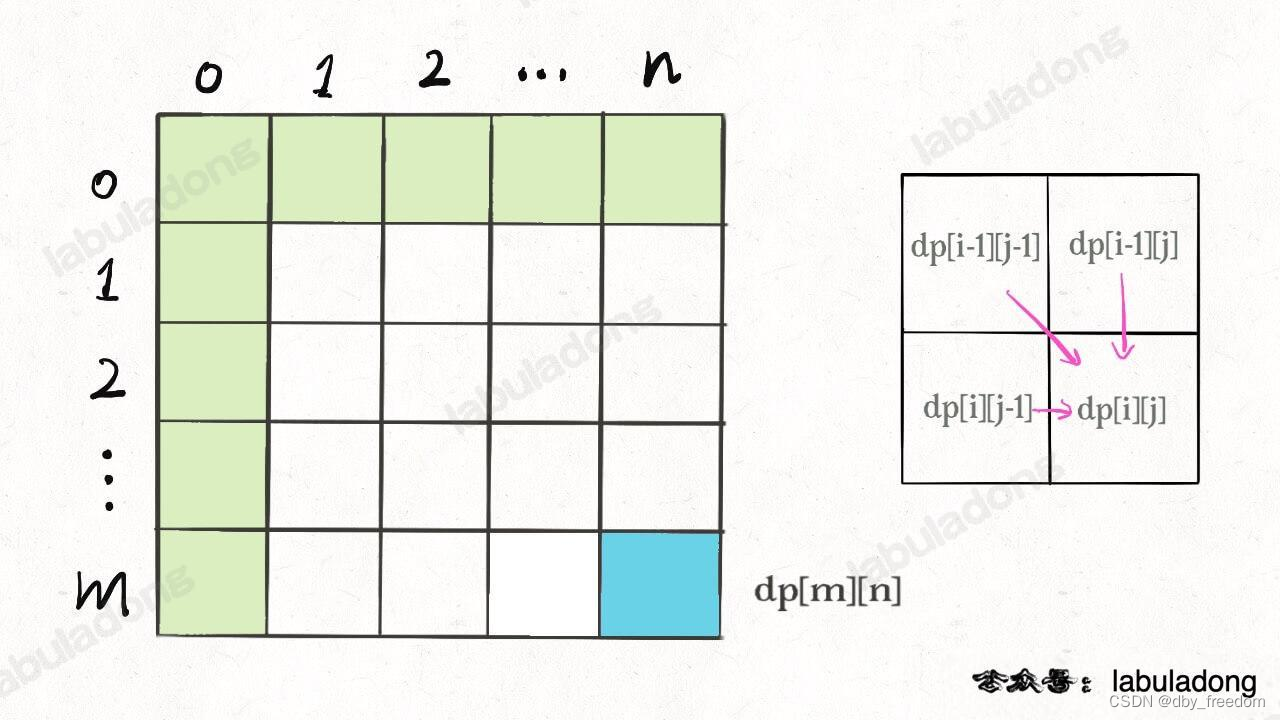
那么，參考剛才說的兩條原則，你該怎么遍歷 dp 數組？肯定是正向遍歷：

for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)// 通過 dp[i-1][j], dp[i][j - 1], dp[i-1][j-1]// 計算 dp[i][j]

因為，這樣每一步迭代的左邊、上邊、左上邊的位置都是 base case 或者之前計算過的，而且最終結束在我們想要的答案 dp[m][n]。

再舉一例，回文子序列問題，詳見后文 子序列問題模板，我們通過過對 dp 數組的定義，確定了 base case 處在中間的對角線，dp[i][j] 需要從 dp[i+1][j], dp[i][j-1], dp[i+1][j-1] 轉移而來，想要求的最終答案是 dp[0][n-1]，如下圖：

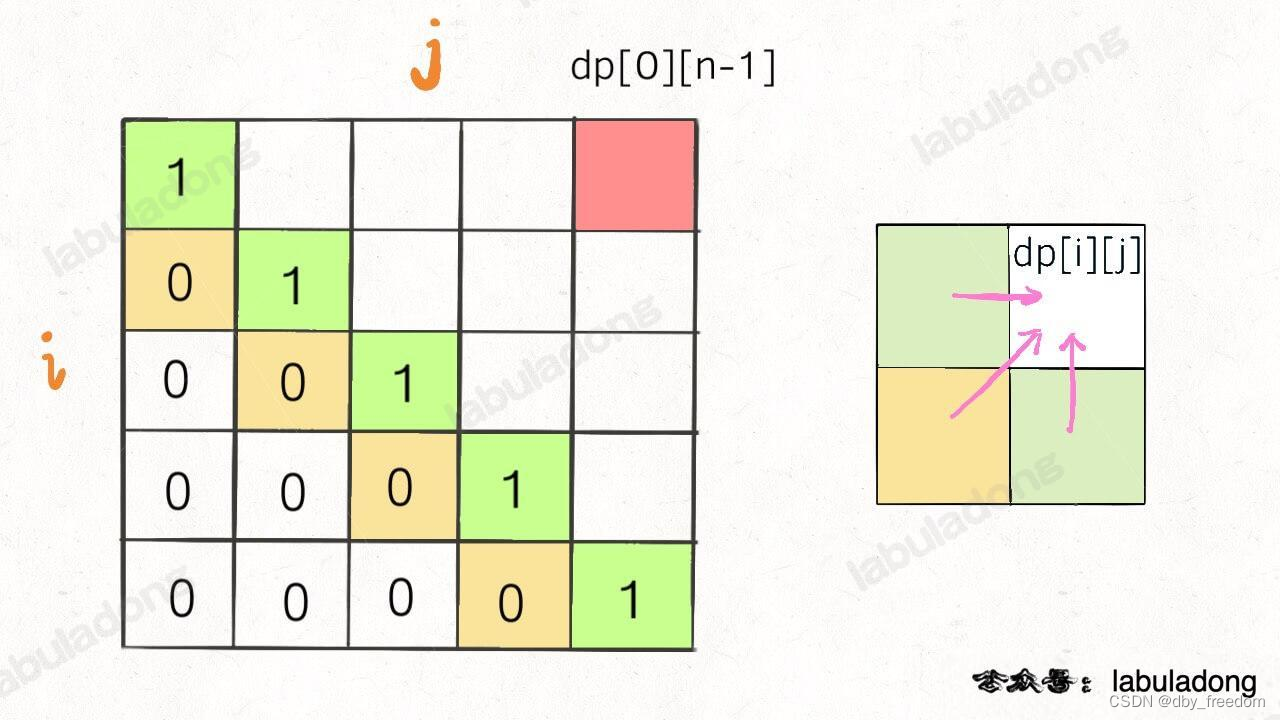
這種情況根據剛才的兩個原則，就可以有兩種正確的遍歷方式：

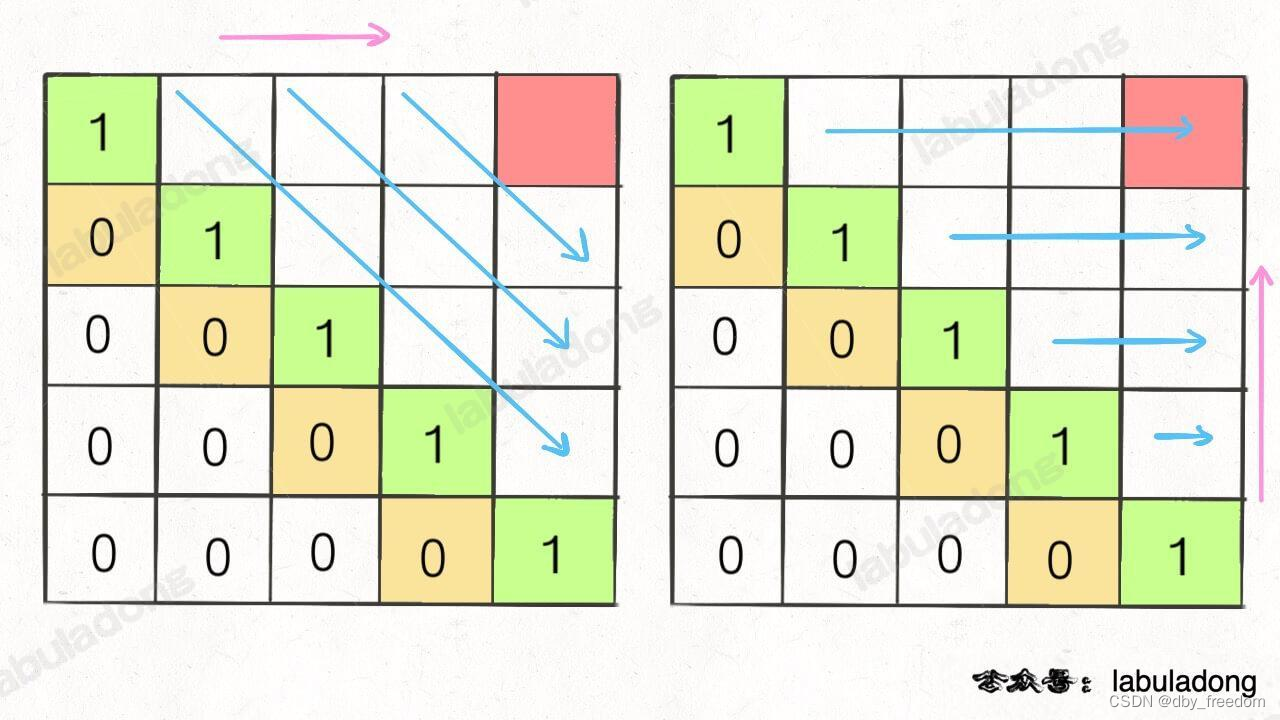
要么從左至右斜著遍歷，要么從下向上從左到右遍歷，這樣才能保證每次 dp[i][j] 的左邊、下邊、左下邊已經計算完畢，得到正確結果。

現在，你應該理解了這兩個原則，主要就是看 base case 和最終結果的存儲位置，保證遍歷過程中使用的數據都是計算完畢的就行，有時候確實存在多種方法可以得到正確答案，可根據個人口味自行選擇。

注：dp 遍歷方向的本質原則就是 以已知推未知，同時需要保證遍歷結束時候，存儲結果的位置必須已經計算出來；

五、參考文獻

1. 最優子結構原理和 dp 數組遍歷方向